Two satellities 1and2 orbiting with the time periods T1andT2, respectively, lie on the same line as shown in (Fig. 5.167). After what minimum time, again the satellities will remain on the same line ? Assume that the two satellities should lie in same side of the center of their concentric circular paths.
 .
.
Let the satellities 1and2 describe angles θ1andθ2 at the center of earth during a time t, respectively. Suppose 2 is ahead of by 1 by an angle θ. Hence, we can write
θ=θ2−θ1
They will be again lie on same line after a minimum time T' sat. For this θ=2π. This gives θ2−θ1=2π. Dividing T' in both sides,
we have θ2T'−θ1T'=2πT'
Substituting θ2T'=ω2andθ1T'=ω1, we have
2πT'=ω2−ω1 where ω2=2πT2 and ω1=2πT1.
Then, 1T'=1T2−1T1
This gives T'=T1T2T1−T2

Topper's Solved these Questions
- KINEMATICS-2Book:CENGAGE PHYSICSChapter:KINEMATICS-2Exercise:Exercise Subjective
Explore 40 Videos
- KINEMATICS-2Book:CENGAGE PHYSICSChapter:KINEMATICS-2Exercise:Exercise Single Correct
Explore 76 Videos
- KINEMATICS-2Book:CENGAGE PHYSICSChapter:KINEMATICS-2Exercise:Exercise 5.3
Explore 12 Videos
- KINEMATICS-1Book:CENGAGE PHYSICSChapter:KINEMATICS-1Exercise:Integer
Explore 9 Videos
- KINETIC THEORY OF GASESBook:CENGAGE PHYSICSChapter:KINETIC THEORY OF GASESExercise:Compression
Explore 2 Videos
Similar Questions
Two particles have time periods T and 5T/4. They start SHM at the same time from the mean postion. After how many oscillations of the particle having smaller time period, they will be again in the same phase ?
View SolutionGiven ratio of time period T1T2. For the two systems shown here is √x. Find x
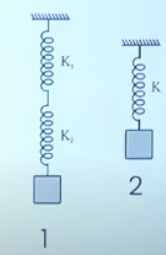
View Solution
Knowledge Check
Two pendulums have time periods T and 5T/4. They start SHM at the same time from the mean position After how many oscillations of the smaller pendulum they will be again in the same phase:
A5B4C11D9If (sinθ,cosθ) and (3,2) lie on the same side of the line x+y=1, then θ lies between
A(0,π2)B(0,π)C(π4,π4)D(0,π4)The range of values of α in the interval (0,π) such that the points (3,5) and (sinα,cosα) lie on the same side of the line x+y−1=0 is
A(0,π/4)B(π/4,π/2)C(0,π/2)DNone
Two satellites A and B are orbiting around the earth in ciruclar orbits of the same radius. The mass of A is 16 times that of B. Then the raito of the period of revolution of B to that of A is
View SolutionFind the value of t for which the points (1,-1),(3,-3) and (t,2) lie on the same line (using determinants).
View SolutionIf (sinθ,cosθ)and(3,2) lie on the same side of the line x+y=1, then θ lies between
View SolutionTwo satellite A and B are travelling in the same plane and same sense in circular orbit around the earth at an atitude rA and rB from the centre of the earth respectively. If at time t=0 the satellite are aligned as shown in the figure, knowing that the radius of the earth R. Determine the time at which again the satellite will be aligned as they were at t=0
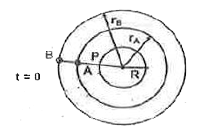
View SolutionTwo radioactive samples of different elements (half-lives t1 and t2 respectively) have same number of nuclei at t=0. The time after which their activities are same is
View Solution

