A projectile is thrown into space so as to have maximum horizontal range R. Taking the point of projection as origin, find out the co-ordinates of the point where the speed of the particle is minimum.
For maximum horizont5al range, θ=45∘.
From R=4Hcotθ=4H [ As θ=45∘. For maximum range.]
Speed of the particle will be minimum at the highest point of parabola.
So the co- ordinate of the highest point will be (R/2,R/4).
 .
.
Topper's Solved these Questions
- KINEMATICS-2Book:CENGAGE PHYSICSChapter:KINEMATICS-2Exercise:Exercise 5.2
Explore 25 Videos
- KINEMATICS-2Book:CENGAGE PHYSICSChapter:KINEMATICS-2Exercise:Exercise 5.3
Explore 12 Videos
- KINEMATICS-2Book:CENGAGE PHYSICSChapter:KINEMATICS-2Exercise:Solved Examples
Explore 7 Videos
- KINEMATICS-1Book:CENGAGE PHYSICSChapter:KINEMATICS-1Exercise:Integer
Explore 9 Videos
- KINETIC THEORY OF GASESBook:CENGAGE PHYSICSChapter:KINETIC THEORY OF GASESExercise:Compression
Explore 2 Videos
Similar Questions
A particle is thrown with a velocity 10m/s and its horizontal range is 5m. Find angle/angles of the projection.
View SolutionA man standing on a hill top projects a stone horizontally with speed v0 as shown in figure. Taking the co-ordinate system as given in the figure. Find the co-ordinates of the point where the stone will hit the hill surface.
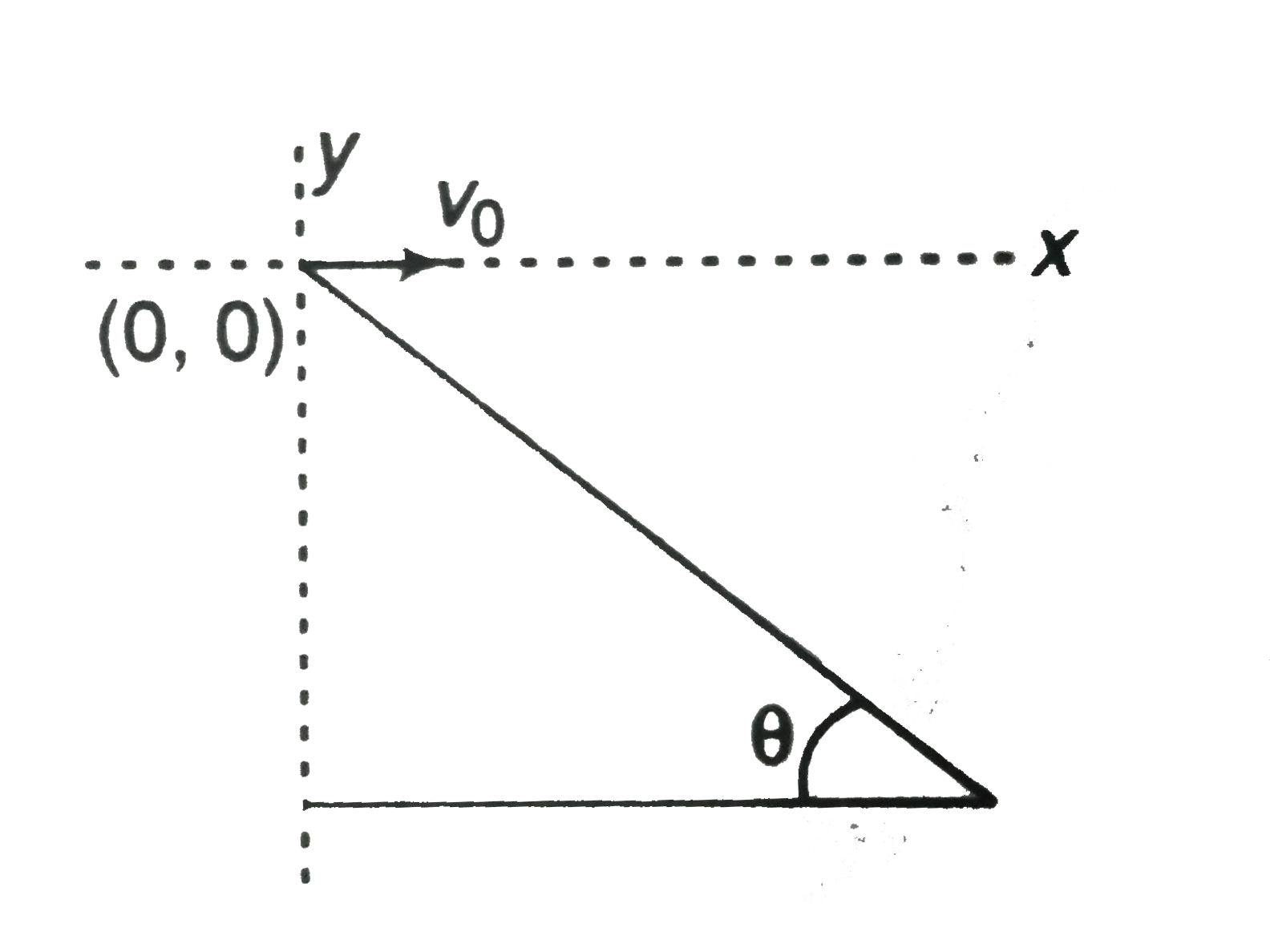
View Solution
Knowledge Check
A projectile is thrwon into space so as to have the maximum possible horizontal range equal to 400m. Taking the point of projection as the origin, the coordinates of the point where the velocity of the projectile is minimum are:-
A-400100B-200100C-400200D-200200A projectile is thrown into air so as to have the maximum possible range equal to 200. Taking projection point as origin, the coordinates of the point where the velocity of the projectile is minimum, are
A(200,50)B(100,50)C(100,50)D(100,100)A projectile is projected with a kinetic energy K. If it has the maximum possible horizontal range, then its kinetic energy at the highest point will be
AK/4BK/2C3K/4DK
An object is projected so that its horizontal range R is maximum. If the maximum height of projectile is H, find the value of H/R.
View SolutionA particle is projected so as to have a range R on a horizontal plane through the point of projection and the greatest height attained by it is h. The maximum horizontal range with this velocity of projection is
2h+R28h or u={2g(h+R216h)}1/2
View SolutionA particle when thrown obliquely from ground, can have a maximum horizontal range 'X'. When it is thrown vertically upwards with the same speed, the maximum height reached by the particle, will be 2 Х 2x √2
View SolutionA particle having mass m is projected with a velocity v0 from a point P on a horizontal ground making an angle θ with horizontal. Find out the torque about the point of projection acting on the particle when
it is at its maximum height ?
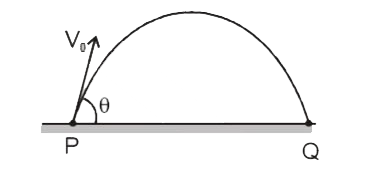
View SolutionA particle is thrown horizontally from a tower of height 20m. If the speed of projection is 20ms then the distance of point from the tower,where the particle hit the ground is:-
View Solution

