A particle starts from the origin with a velocity of 10ms−1 and moves with a constant acceleration till the velocity increases to 50ms−1. At that instant, the acceleration is suddenly reversed. What will be the velocity of the particle, when it returne to the starticng point?
Zero
10ms−1
50ms−1
70ms−1
The correct Answer is:D
To solve the problem step by step, we will use the equations of motion.
Step 1: Determine the acceleration during the first phase of motion
The particle starts from the origin with an initial velocity U=10m/s and accelerates to a final velocity V=50m/s. We can use the third equation of motion:
V2=U2+2ax
Where:
- V=50m/s
- U=10m/s
- a is the acceleration
- x is the displacement during this phase
Substituting the known values:
(50)2=(10)2+2ax
Calculating the squares:
2500=100+2ax
Rearranging gives:
2ax=2500−100
2ax=2400
ax=1200(1)
Step 2: Determine the final velocity after the acceleration is reversed
Now, when the acceleration is suddenly reversed, the initial velocity for this phase is U=50m/s. We want to find the final velocity V when the particle returns to the starting point (displacement −x).
Using the third equation of motion again:
V2=U2+2(−a)(−x)
Substituting the known values:
V2=(50)2+2(−a)(−x)
V2=2500+2ax
From equation (1), we know ax=1200:
V2=2500+2(1200)
V2=2500+2400
V2=4900
Step 3: Calculate the final velocity
Taking the square root to find V:
V=√4900
V=70m/s
Thus, the velocity of the particle when it returns to the starting point is 70m/s.
Final Answer
The final velocity of the particle when it returns to the starting point is 70m/s.
---
- V=50m/s
- U=10m/s
- a is the acceleration
- x is the displacement during this phase
2ax=2400
ax=1200(1)
V2=2500+2ax
V2=2500+2400
V2=4900
V=70m/s
The final velocity of the particle when it returns to the starting point is 70m/s.
Topper's Solved these Questions
- KINEMATICS-1Book:CENGAGE PHYSICSChapter:KINEMATICS-1Exercise:Graphical Concept
Explore 17 Videos
- KINEMATICS-1Book:CENGAGE PHYSICSChapter:KINEMATICS-1Exercise:Graphical cancept
Explore 1 Video
- KINEMATICS-1Book:CENGAGE PHYSICSChapter:KINEMATICS-1Exercise:Subjective
Explore 29 Videos
- GRAVITATIONBook:CENGAGE PHYSICSChapter:GRAVITATIONExercise:INTEGER_TYPE
Explore 1 Video
- KINEMATICS-2Book:CENGAGE PHYSICSChapter:KINEMATICS-2Exercise:Exercise Integer
Explore 9 Videos
Similar Questions
A body starts with an initial velocity of 10ms-1 and is moving along a straight line with constant acceleration. When the velocity of the particle is 50ms- the acceleration is reversed in direction. The speed of the particle when it again reaches the starting point is
View SolutionA particle starts from origin at t=0 with a velocity of 15ˆims−1 and moves in xy-plane under the action of a force which produces a constant acceleration of 15ˆi+20ˆjms−2. Find the y-coordinate of the particle at the instant its x-coordinate is 180 m.
View Solution
Knowledge Check
In the Q. 122 what will be the velocity of the particle when it returns to the starting point?
A→r0B−→r0C2→r0D−2→r0A particle starting from rest attains a velocity of 50ms−1 in 5 s. The acceleration of the particle is
A5ms2B10ms2C50ms2D100ms2A particle starts from rest and moves with constant acceleration. Then velocity displacement curve is:
A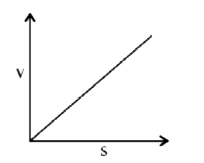 B
B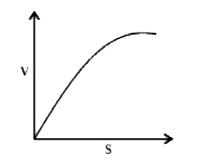 C
C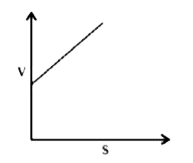 D
D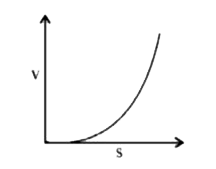
A particle is moving eastwards with a velocity of 5ms−1. In 10seconds the velocity changes to 5ms−1 northwards. The average acceleration in this time is
View SolutionA particle starts from the origin at t=Os with a velocity of 10.0ˆjm/s and moves in the xy-plane with a constant acceleration of (8ˆi+2ˆj)m/s−2. What time is the x-coordinate of the particle 16m?
View SolutionStarting from rest, the acceleration of a particle is a=2(t-1). The velocity of the particle at t=5s is :-
View SolutionStarting from rest, acceleration of a particle is a=2t(t−1). The velocity of the particle at t=5s is
View SolutionA particle starting from rest moves along a straight line with constant acceleration for this velocity displacement graph will have the form-
View Solution

