In the relation , the dimensional formula for is
A
B
C
D
Video Solution
Text Solution
The correct Answer is:D
Here is dimensionless because it is argument of a trigonometric function.
|
Topper's Solved these Questions
- DIMENSIONS & MEASUREMENTBook:CENGAGE PHYSICSChapter:DIMENSIONS & MEASUREMENTExercise:Multiple Correct
Explore 2 Videos
- DIMENSIONS & MEASUREMENTBook:CENGAGE PHYSICSChapter:DIMENSIONS & MEASUREMENTExercise:Linked Comprehension
Explore 3 Videos
- DIMENSIONS & MEASUREMENTBook:CENGAGE PHYSICSChapter:DIMENSIONS & MEASUREMENTExercise:Subjective
Explore 31 Videos
- CENTRE OF MASSBook:CENGAGE PHYSICSChapter:CENTRE OF MASSExercise:INTEGER_TYPE
Explore 1 Video
- FLUID MECHANICSBook:CENGAGE PHYSICSChapter:FLUID MECHANICSExercise:INTEGER_TYPE
Explore 1 Video
Similar Questions
Knowledge Check
In the relation y=rsin(ωt−kx), the dimensions of ω/k are
A[M0L0T0]B[M0L1T−1]C[M0L0T1]D[M0L1T0]If i1=i0sin(ωt),i2=i02sin(ωt+ϕ), then i3=
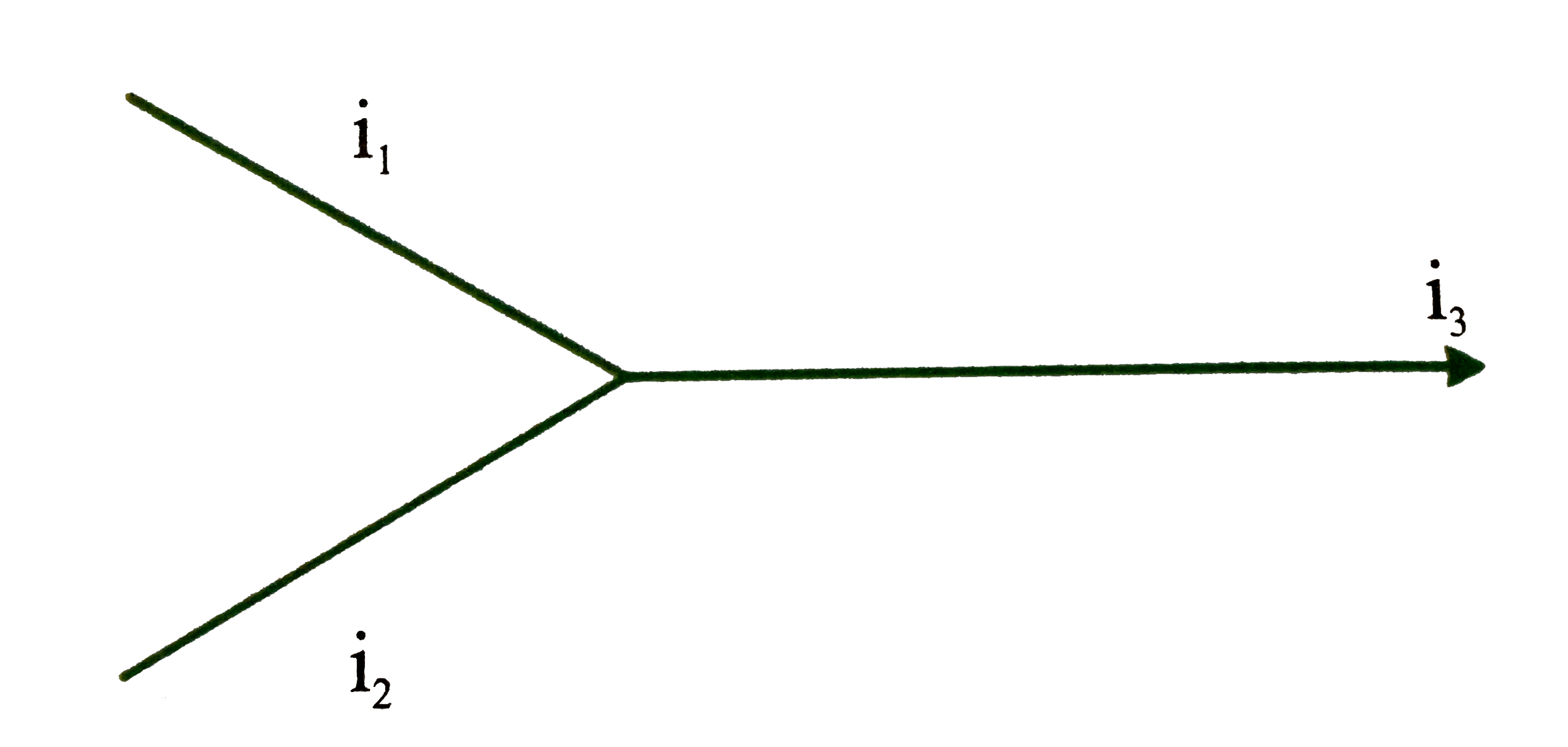 A√i201+i202sin{ϕ+ωt}B(i01+i02)sin(ϕ2+ωt)C(√i201+i202+2i01i02cosϕ)sin[ϕ+ωt]D(√i201+i202+2i01i02cosϕ)sin[α+ωt] where α=Tan−1[i02sinϕi01+i02cosϕ]
A√i201+i202sin{ϕ+ωt}B(i01+i02)sin(ϕ2+ωt)C(√i201+i202+2i01i02cosϕ)sin[ϕ+ωt]D(√i201+i202+2i01i02cosϕ)sin[α+ωt] where α=Tan−1[i02sinϕi01+i02cosϕ]What are the dimensional formulae of ω and K in the relation y=Asin(ωt−Kx)?
A[M0L0T2][M0L−1T0]B[M0L0T−1][M0L−1T0]C[M0L0T−1][M0L1T0]D[M0L0T−1][M0L1T−1]
In y= A sin ωt + A sin (ωt+(2π)/3) match the following table.
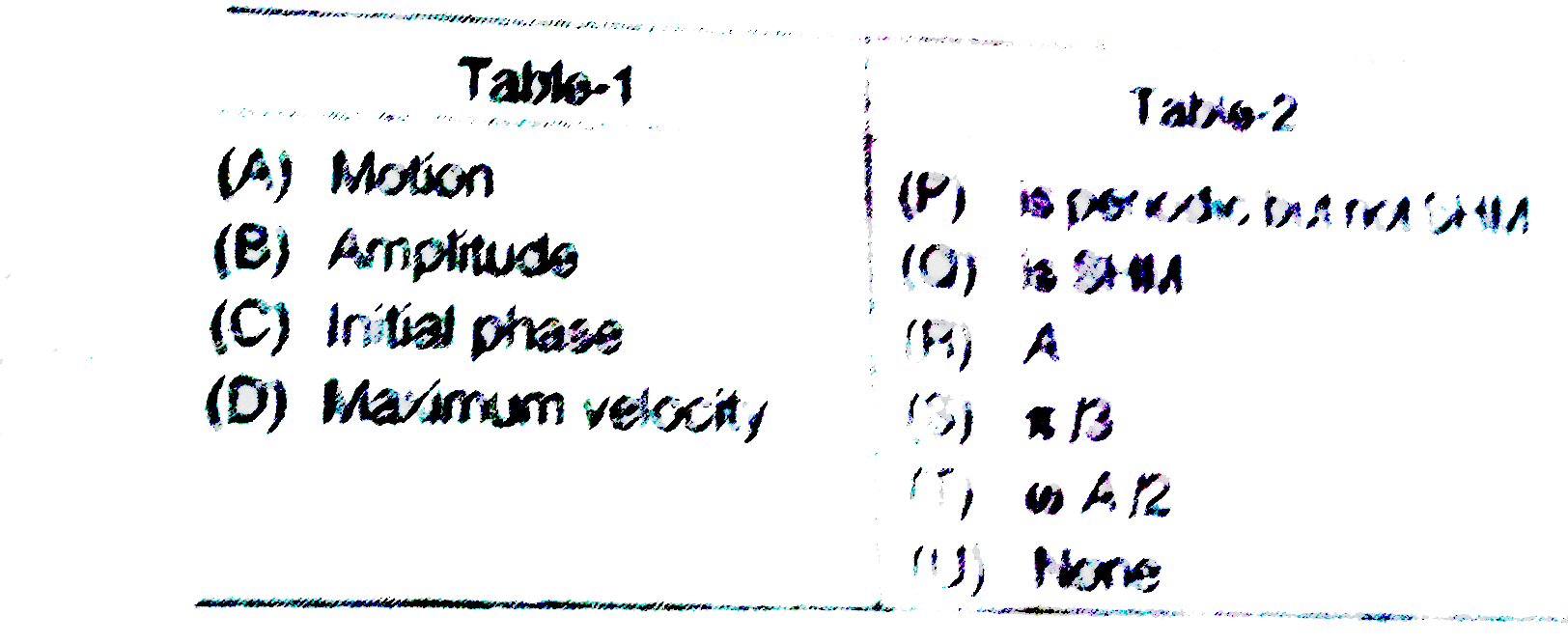
View SolutionThree sinusoidal displacements are applied in X-direction to a point mass in such a way that total displacement is zero and the mass comes to rest. What are the values of B and ϕ if the equations are
x1(t)=Asin2ωt
x2(t)=Asin(2ωt+4π3)
x3(t)=Bsin(2ωt+ϕ)
View SolutionCheck the correctness of the equation : y=asin(ωt+ϕ), where y = displacement , a = amplitude , ω = angular frequency and ϕ is an angle .
View SolutionEvalueta
∫T0E0I0sinωtsin(ωt+ϕ)dt
View SolutionThe displacement of the wave given by equation y(x,t)=asin(kx−ωt+ϕ), whereϕ=0 at point x and t = 0 is same as that at point
View Solution

