Check whether the relation S=ut+12at2 is dimensionally correct or not , where symbols have their usual meaning .
To check whether the relation S=ut+12at2 is dimensionally correct, we will analyze the dimensions of both sides of the equation step by step.
Step 1: Identify the dimensions of S
- The left-hand side (LHS) of the equation is S, which represents distance or displacement.
- The dimension of distance (or displacement) is given by:
(S)=(L)=M0L1T0
Step 2: Analyze the first term on the right-hand side ut
- The first term on the right-hand side (RHS) is ut, where:
- u is the initial velocity.
- The dimension of velocity u is:
(u)=M0L1T−1
- t is time, with the dimension:
(t)=M0L0T1
- Now, we multiply the dimensions of u and t:
(ut)=(u)⋅(t)=(M0L1T−1)⋅(M0L0T1)=M0L1T0=M0L1T0
Step 3: Analyze the second term on the right-hand side 12at2
- The second term is 12at2. The constant 12 is dimensionless, so we only need to consider the dimensions of a and t2:
- a is acceleration, with the dimension:
(a)=M0L1T−2
- t2 has the dimension:
(t2)=(M0L0T1)2=M0L0T2
- Now, we multiply the dimensions of a and t2:
(at2)=(a)⋅(t2)=(M0L1T−2)⋅(M0L0T2)=M0L1T0=M0L1T0
Step 4: Combine the dimensions of the RHS
- Now we can add the dimensions of both terms on the RHS:
(ut+12at2)=(ut)+(12at2)=M0L1T0+M0L1T0=M0L1T0
Step 5: Compare the dimensions of LHS and RHS
- LHS: (S)=M0L1T0
- RHS: (ut+12at2)=M0L1T0
Since the dimensions of both sides are equal, we conclude that the relation S=ut+12at2 is dimensionally correct.
- The left-hand side (LHS) of the equation is S, which represents distance or displacement.
- The dimension of distance (or displacement) is given by:
(S)=(L)=M0L1T0
- The first term on the right-hand side (RHS) is ut, where:
- u is the initial velocity.
- The dimension of velocity u is:
(u)=M0L1T−1
- t is time, with the dimension:
(t)=M0L0T1
- Now, we multiply the dimensions of u and t:
(ut)=(u)⋅(t)=(M0L1T−1)⋅(M0L0T1)=M0L1T0=M0L1T0
- The second term is 12at2. The constant 12 is dimensionless, so we only need to consider the dimensions of a and t2:
- a is acceleration, with the dimension:
(a)=M0L1T−2
- t2 has the dimension:
(t2)=(M0L0T1)2=M0L0T2
- Now, we multiply the dimensions of a and t2:
(at2)=(a)⋅(t2)=(M0L1T−2)⋅(M0L0T2)=M0L1T0=M0L1T0
- Now we can add the dimensions of both terms on the RHS:
(ut+12at2)=(ut)+(12at2)=M0L1T0+M0L1T0=M0L1T0
- LHS: (S)=M0L1T0
- RHS: (ut+12at2)=M0L1T0
Topper's Solved these Questions
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICSCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Exercise 1.1
16 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICSCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Exercise 1.2
6 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - INTEGER_TYPE
1 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICSCHAPTER - FLUID MECHANICSEXERCISE - INTEGER_TYPE
1 Videos
Similar Questions
Knowledge Check
The correct combination is (symbols have their usual meanings)
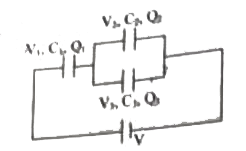 AQ1=Q2=Q3andV1=V2=V3=VBQ1=Q2+Q3andV=V1+V2+V3CQ1=Q2+Q3andV=V1+V2DQ2=Q3andV2=V3
AQ1=Q2=Q3andV1=V2=V3=VBQ1=Q2+Q3andV=V1+V2+V3CQ1=Q2+Q3andV=V1+V2DQ2=Q3andV2=V3Select the incorrect relation. (Where symboles have their usual meanings):-
ACp=γRγ−1BCP−CV=RCΔU=PfVf−PiVi1−γDCv=Rγ−1Choose the correct arrangement, where the symbols have their usual meanings
A→u>up>urmsBurms>→u>upCup>→u>urmsDup>urms>→u
Using velocity time graph, establish the relation s=ut+12at2, where the symbols have their usual meanings.
View SolutionThe correct form of Stroke's law is (symbols have their usual meanings)
View SolutionSelect the incorrect relation. (Where symboles have their usual meanings):-
View SolutionChoose the correct arrangement. The symbols have their usual meanings
View SolutionBohr magnetonis given by (symbols have their usual meanings)
View Solution
