Question

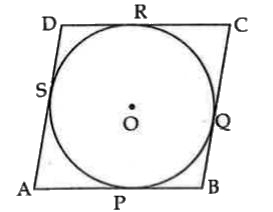
Prove that a parallelogram circumscribing by a circle is always a rhombus.

Explanation

Let ABCD is a parallelogram circumscribing by a circle with centre at O.
We have to prove that ABCD is a rhombus.
Proof: Let the circle touches the parallelogram ABCD at the points P, Q, R and S.
Then AP and AS are two tangents to the circle from the extenrnal point A.
`therefore AP = AS ........(1)`
Similarly, `BP =BQ ......... (2)`
`CQ =CR ...........(3) and `
`DR=DS.........(4)`
Now `because` ABCD is a parallelogram,` therefore AB =DC and AD=BC.`
Now, `AB +DC =AP + BP+DR+CR`
`=AS+BQ+ DS+CQ`
`=AS+ DS+ BQ+ CQ`
`=AD+BC`
or, `AB+AB=BC+BC[becauseDC=AB and AD=BC]`
`or, 2AB =2BC or, AB= BC`
Similarly, `AD= DC, therefore AB= BC=CD=DA`
`therefore` four sides of the parallelogram ABCD are equal ABCD is also a parallelogram
`therefore ABCD` is a rhombus. (Provide)