The tangent drawn at points P and Q on the circumference of a circle intersect at A. If ∠PAQ=60∘, find the value of ∠APQ. Solution in Bengali
Let P and Q be any two points on the circle with centre O. Two tangents AP and AQ drawn at the points P and Q intersect each other at the point A. Let us join P, Q and O, A
Given that ∠PAQ=60∘.
Now, Ap is a tangent to the circle with centre O and OP is the radius passing through the point of contact P.∴OP⊥AP,∴∠OPA=90∘.
Similarly, ∠OQA=90∘
In Δ'sPOAandΔQOA,
∠OPA=∠OQA[∵ each is a right-angle]
OP=OQ[∵ radius of same circle] and hypotenuse OA is common to both
∴ΔPOA≡ΔQOA [by the R-H-S condition of congruency ]
therefero∠OAP=∠OAQ [similar angles of congurent triangles ]
Given that ∠PAQ=60∘or,∠PAO+∠QAO=60∘
or, ∠PAO=60∘∠QAO=∠PAO]
or, 2∠PAO=60∘or,∠PAO=60∘2=30∘
Then, ∠PAO90∘−∠OAP=90∘−30∘=60∘[∵∠OAP=∠PAO=30∘]
∴∠APQ=∠APO−∠OPQ=90∘−30∘=60∘
∴ value of ∠APQ=60∘.

Topper's Solved these Questions
- THEOREMS RELATED TO TANGENT IN A CIRCLE BOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO TANGENT IN A CIRCLE EXERCISE - EXERCISE 4.1
20 Videos
- THEOREMS RELATED TO TANGENT IN A CIRCLE BOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO TANGENT IN A CIRCLE EXERCISE - EXERCISE 4.2
23 Videos
- THEOREMS RELATED TO ANGLES IN A CIRCLEBOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO ANGLES IN A CIRCLEEXERCISE - EXERCISE 2.3 (Long Answer Type Questions)
14 Videos
- TRIGONOMETRIC RATIOS AND TRIGONOMETRIC IDENTITIES BOOK - CALCUTTA BOOK HOUSECHAPTER - TRIGONOMETRIC RATIOS AND TRIGONOMETRIC IDENTITIES EXERCISE - EXERCISE
66 Videos
Similar Questions
PR and PS are two tangents drawn from a extental point P of the Circle with centre at O. If PR=8cmand∠RPO=60∘, then the length of PS=
View SolutionThe distance of the point from the centre of a circle with diameter of 16 cm is 17 cm. Then the length of the tangent from the point to the circle is
View SolutionProve that angle in the segment of a circle which is greater than a semi-circle is an acute angle.
View SolutionIf tanθ=pq, what is the value of psecθ−q cosecθpsecθ+q cosecθ=
View SolutionA pair of tangents are drawn to a unit circle with centre at the origin and these tangents intersect at point P enclosing an angle of 60^(@) . The area enclosed by the tangents and the arc of the circle is,
View SolutionP केंद्र वाले, वृत्त के व्यास AB के अंतिम बिन्दुओ पर दो स्पर्श रेखाएं खींची गई। यदि बिंदु C से वृत्त पर खींची गई स्पर्श रेखा, अन्य दो स्पर्श रेखाओ को Q तथा R पर प्रतिछेदित करती है। ∠QPR का मान ज्ञात करे?
View Solutionमाना कि केंद्र बिन्दु O वाले वृत्त पर P और Q दो बिन्दू है । यदि वृत्त के दो बिन्दू P और Q से होकर खींची गई स्पर्श रेखाएं A पर मिलती है, तो ∠PAQ=48∘,then ∠APQ कितना होगा ?
View Solutionदो सर्वांगसम वृत्त परस्पर बिंदुओं A और B पर प्रतिच्छेद करते है । A से होकर कोई रेखाखंड PAQ इस प्रकार खींचा गया है कि P और Q दोनों वृत्तों पर स्थित है । सिद्ध कीजिए कि BP=BQ है ।
View Solutionदिये गए चित्र में O केन्द्र वाले एक वृत्त के बिन्दु A पर PAQ एक स्पर्शी है तथा ∠BAQ=60∘ तब ∠ABC का मान ज्ञात कीजिए ।
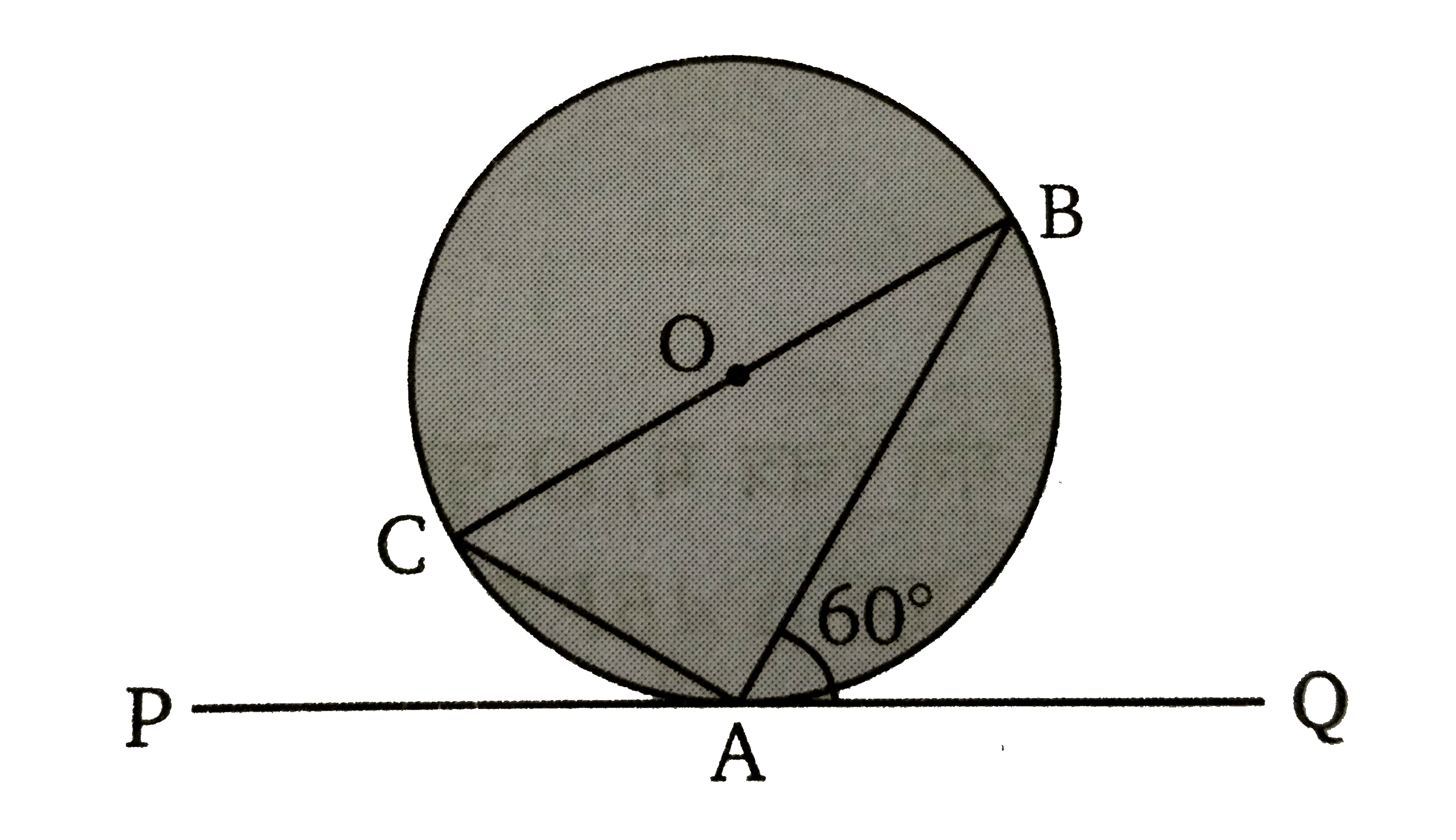
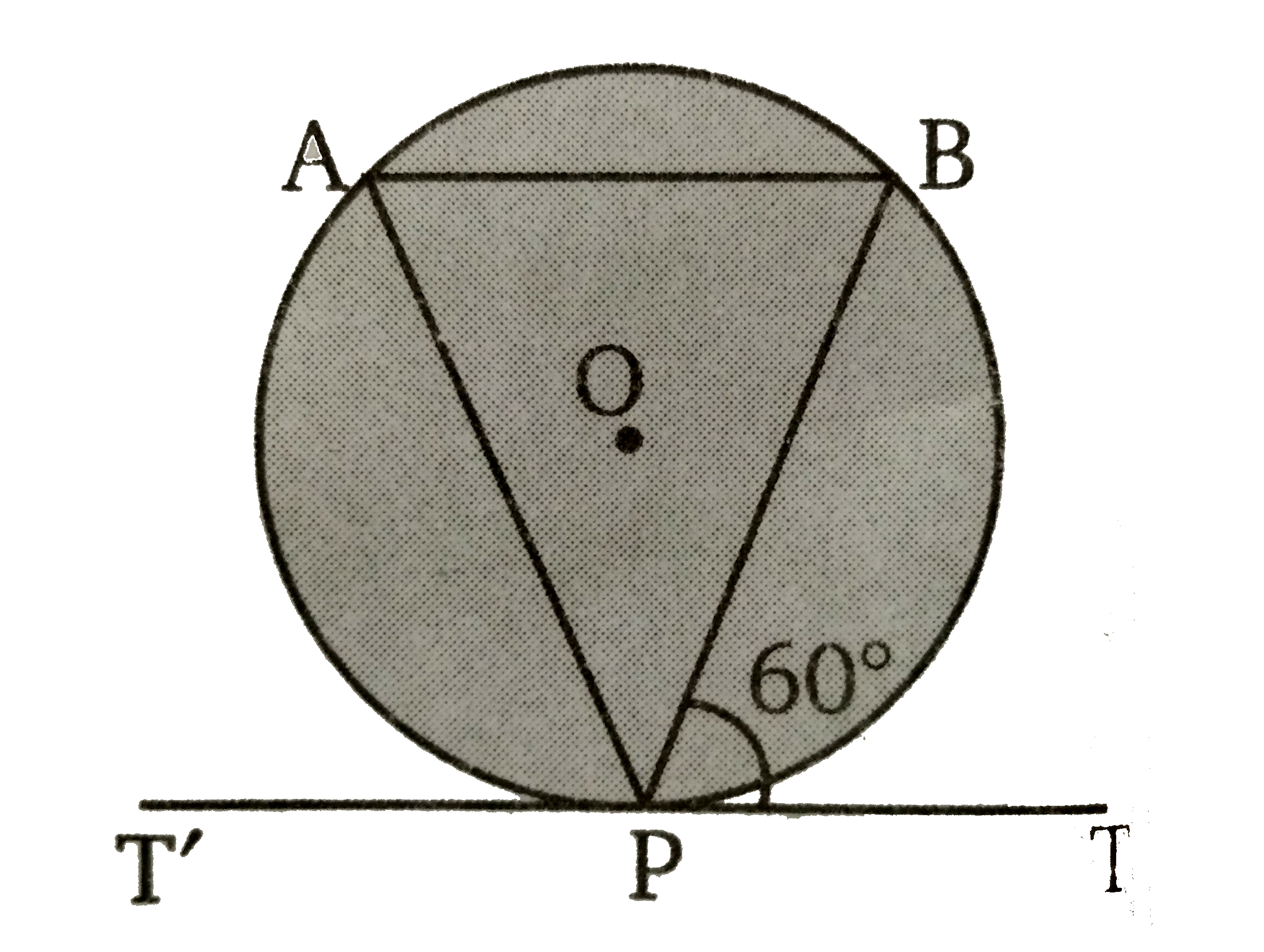
View Solutionदिये गए चित्र में, O वृत्त का केन्द्र है तथा वृत्त के बिन्दु P पर T'PT एक स्पर्शी है। इसके अन्दर एक △ABP खींचा गया है। यदि ∠BPT=60∘ तब ∠BAP का मान ज्ञात कीजिए ।
View SolutionXY is a diameter of a circle. PAQ is a tangent to the circle at the point A lying on the circumference. The perpendicular drawn on the tangent to the circle from X intersects PAQ at Z. Prove that XA is a bisector of ∠YXZ. [GP−X]
View SolutionTwo chords AC and BD of a circle intersect each other at the point O. If two tangents drawn at the points A and B intersect each other at the point P and two tangents drawn at the points C and D intersect at the point Q, prove that ∠P+∠Q=2∠BOC.[GP−X]
View SolutionIn the figure, O is the centre and BOA is a diameter of the circle. A tangent drawn to the circels at the point P intersects the extended BA at the point T. If ∠PBO=30∘, find the value of ∠PAT.
View SolutionTwo tangents drawn at the point A and B on a circle intersect each other at the point P. If ∠APB=60∘, then ∠PAB=
View Solutionयदि O केन्द्र और a त्रिज्या के वृत्त पर बाह्य बिन्दु P से खींची गई दो स्पर्श रेखाओं के मध्य कोण 60∘ है, तो OP की लम्बाई ज्ञात कीजिए।
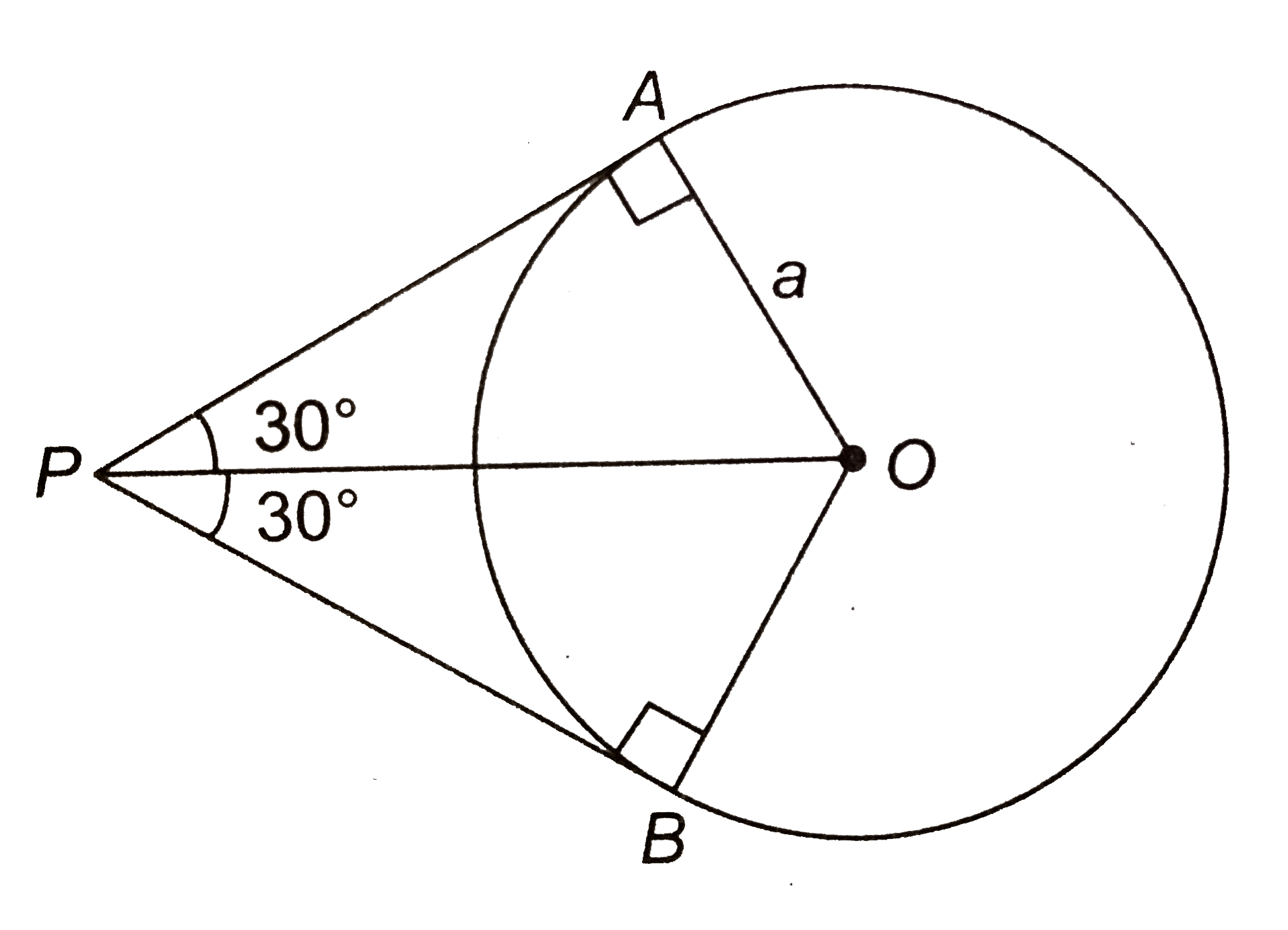
View SolutionTwo tangent are drawn from external point P to circle of radius 3 , such that angle between them is 60^@ , then length of tangents is
View Solution
