In the adjoining figure, O is the center of the circle and AC is a diameter of it If DC||EB, ∠AOB=80∘and∠ACE=10∘ , then find the value of angleBED.Solution in Bengali
Given that DC||EB and CE is their transversal.
∴∠DCE=∠BEC[∵alternate angle] . . . . . . . .(1)
Now , ∠AOB=2∠ACB[∵ central angle is twice of angle of angle in circle]
Math (X)-20
or, 80∘=2∠ACB[∵∠AOB=80∘given]
or ∠ACB=80∘2=40∘
Also ∠BOC=180∘−∠AOB=180∘−80∘=100∘
Again , the central angle produced by the chord ⌢BC is ∠BOC and angle in circle is ∠BEC
∴∠BEC=12∠BOC=12×100∘=50∘[∵∠BOC=100∘]
∴∠ECD=50∘ [by (1)]
Also , ∠BED+∠BCD=180∘[∴ BCDE is a cyclic quadrilateral]
or, ∠BED=180∘−∠BCD=180∘−100∘=80∘
[∵∠BCD=∠ACB+∠ACE+∠ECD=40∘+10∘+50∘=100∘]∴∠BED=80∘

Topper's Solved these Questions
- THEOREMS RELATED TO CYCLIC QUADRILATERAL Book:CALCUTTA BOOK HOUSEChapter:THEOREMS RELATED TO CYCLIC QUADRILATERAL Exercise:Example (Long-answer type questions)
Explore 20 Videos
- THEOREMS RELATED TO CYCLIC QUADRILATERAL Book:CALCUTTA BOOK HOUSEChapter:THEOREMS RELATED TO CYCLIC QUADRILATERAL Exercise:EXERCISE-3(Very short - answer type questions)(MCQ)
Explore 4 Videos
- THEOREMS RELATED TO CYCLIC QUADRILATERAL Book:CALCUTTA BOOK HOUSEChapter:THEOREMS RELATED TO CYCLIC QUADRILATERAL Exercise:Fill in the blanks:
Explore 6 Videos
- THEOREMS RELATED TO CIRCLE Book:CALCUTTA BOOK HOUSEChapter:THEOREMS RELATED TO CIRCLE Exercise:EXERCISE - 1 (Long - answer type question )
Explore 9 Videos
- THEOREMS RELATED TO ANGLES IN A CIRCLEBook:CALCUTTA BOOK HOUSEChapter:THEOREMS RELATED TO ANGLES IN A CIRCLEExercise:EXERCISE 2.3 (Long Answer Type Questions)
Explore 14 Videos
Similar Questions
In the adjoining figure , the diagonals of the cyxlic quadrilateral PQRS intersect each other at the point X in such a way that ∠PRS=65∘and∠ROS=45∘. Find the values of ∠SQPand∠RSP .
View SolutionIf the length of diagonal of a square is √72cm, then calculate the area of the square.
View SolutionAll angles in the same segment are……….
View SolutionProve that diameter is the greatest chord of a circle.
View SolutionProve that angle in the segment of a circle which is greater than a semi-circle is an acute angle.
View SolutionIn the adjoining figure O is the centre of the circle and ∠AOB=100∘. Find the value of ∠BCD.
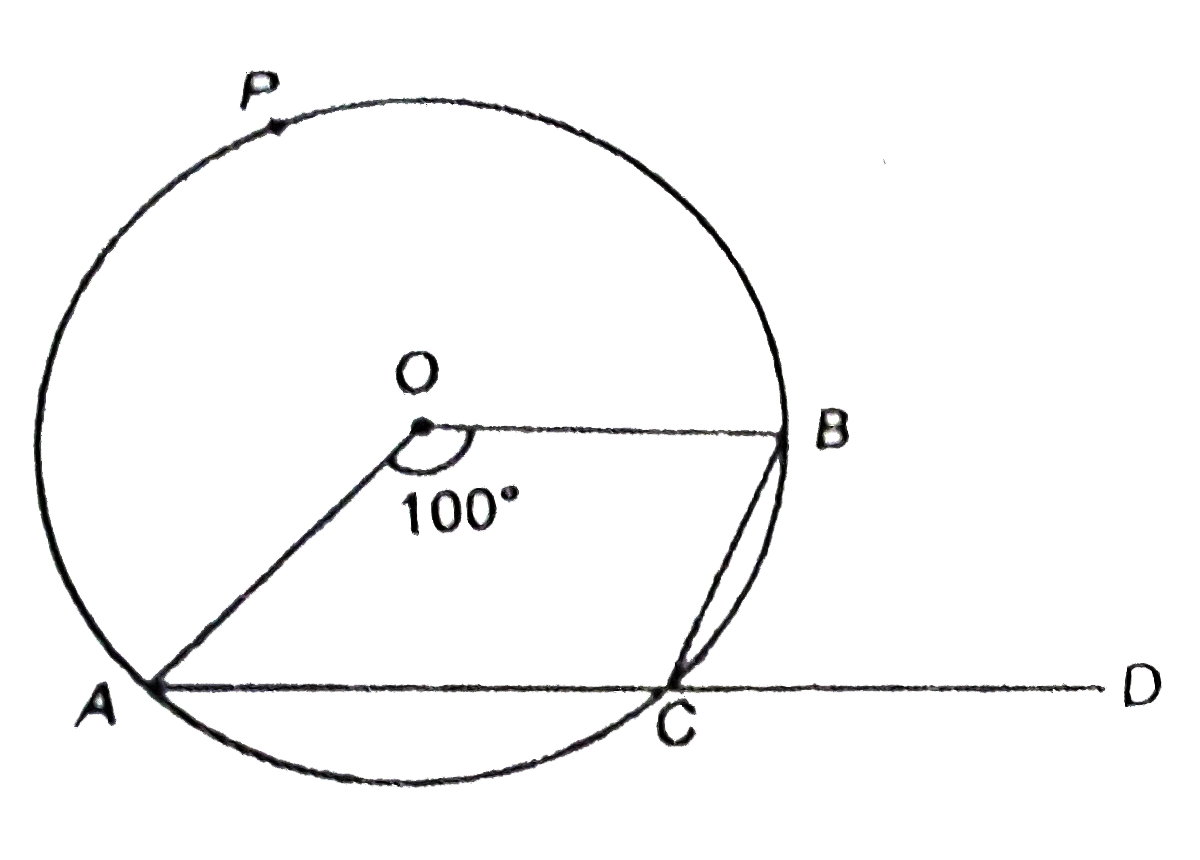
View SolutionIn the adjoining figure , O is the centre of the circle. If ∠ACB=25∘, then find ∠AOB.
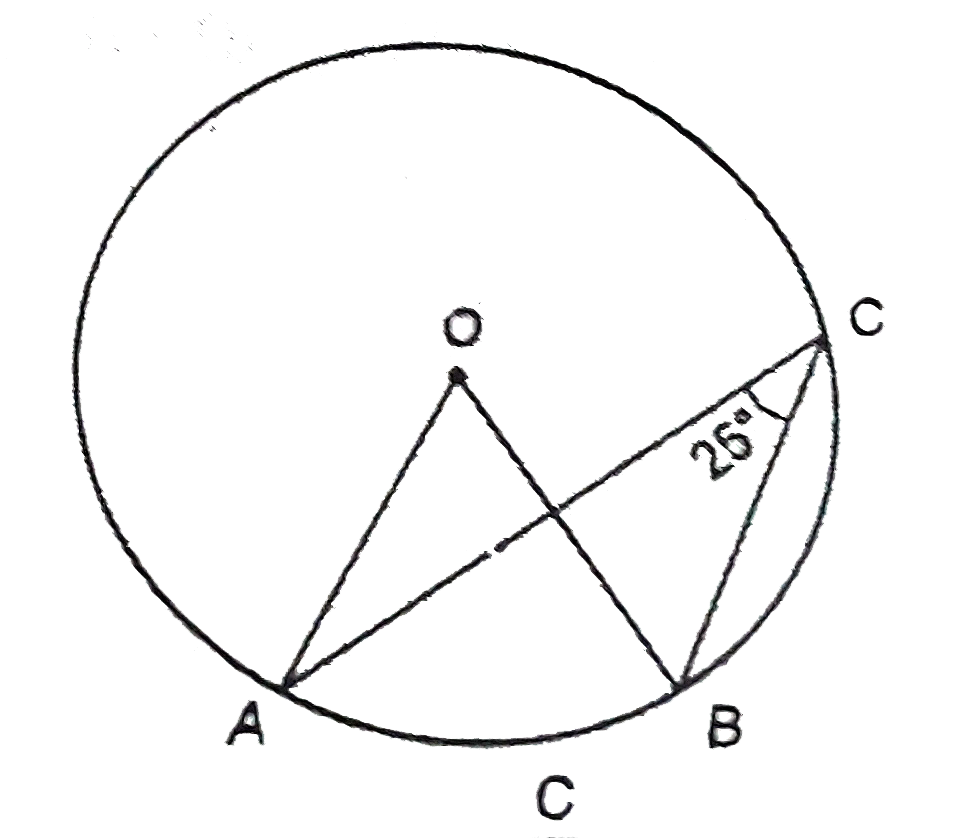
View SolutionIn the adjoining figure, O is the centre of the circle and AB is its diameter. If AC=8 cm and BC= 6cm, then find the radius of the circle.

View SolutionIn the adjoining figure, O is the centre of the circle. If ∠PAO=15∘ and ∠PBO=30∘, then find the value of ∠AOB.

View SolutionIn the adjoining figure, O is the centre of the circle. If ∠AOB=70∘, then find the value of ∠OCD.

View Solutionसंलग्न चित्र में, 'O' वृत्त को केन्द्र तथा ∠AOB=100∘ है | ∠BCD का मान ज्ञात कीजिए |
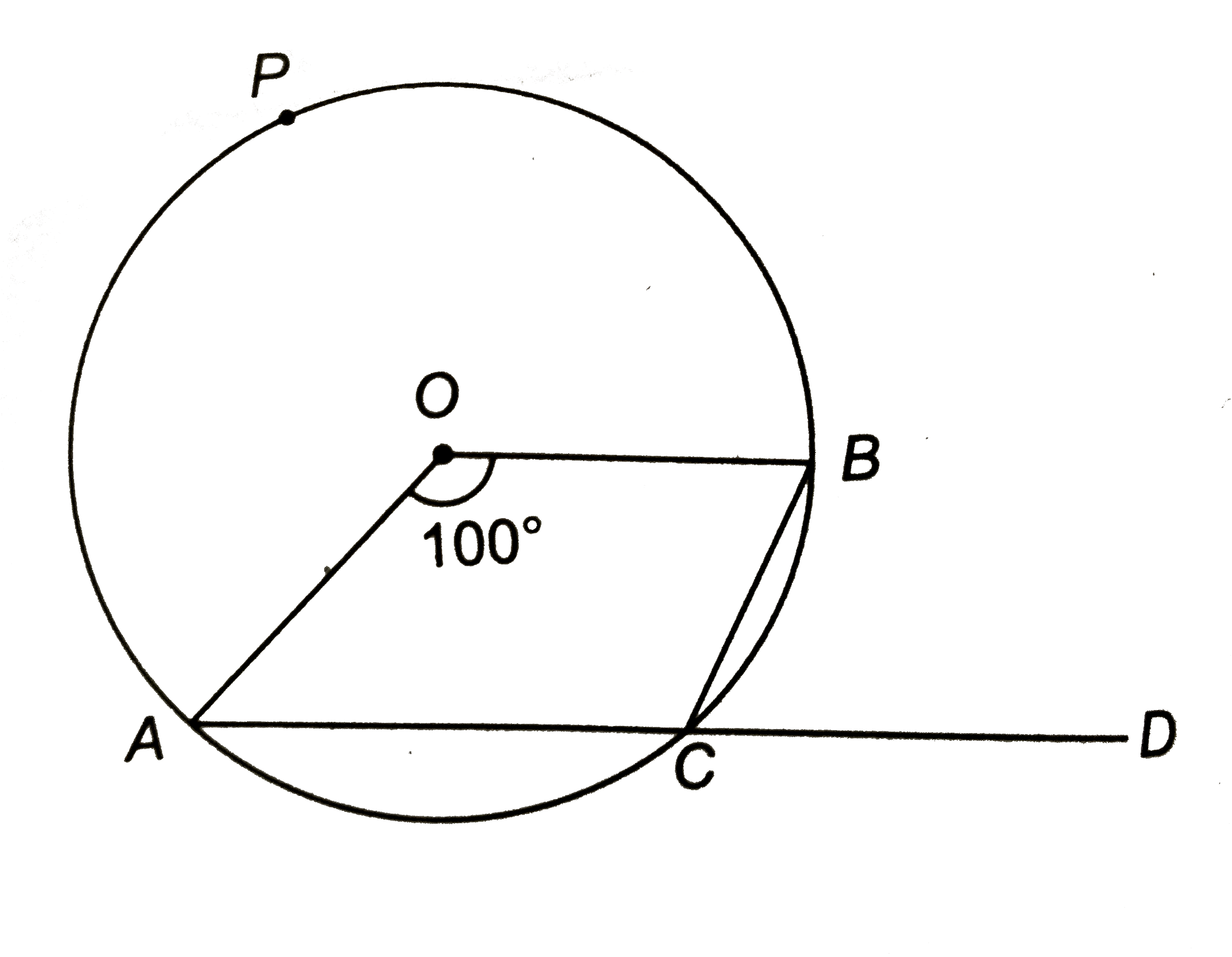
View SolutionIn the adjoining figure, O is the centre of the circle AC is a diameter and chord DE is parallel to the diameter AC. If ∠CBD=60∘ , find the value of ∠CDE
View SolutionIn the adjoining figur , O is the center of the circle and AB is one of its diameter. ABCD is a cyclic quadrilateral in wich AB||DC and if ∠BAC=25∘ , then the value of ∠DAC IS
View SolutionIn the adjoining figure ,O is the center of the circle and AB is a diameter. If ∠AOD=140∘and∠CAB=50∘, then find value of ∠BED
View Solutionदी गई आकृति में O वृत्त का केंद्र है| ∠AOB=60∘ है| ACB का मान क्या है?
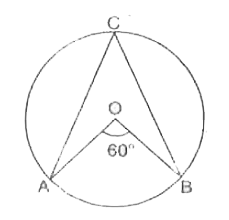
View Solution

