The two circles with centre X and Y intersect each other at the points A and B, A joined with the mid -point S of XY and the perpendicular on SA through the point A is drawn which intersect the two circles at the point P and Q .Prove that PA = AQ.Solution in Bengali
Let us draw two perpendicular XM and YN on PA and AQ respectively. Let us join X, A and Y, A
∵XM⊥PA,∴AM=12PA……….(1)
Again YM⊥PA,∴AN=12AQ……….(2)
Now , ∵ S is the mid-point XY.
∴AS⊥XY[∵ the line segment joining two centres of two circles bisect their common chord in right angles ] .
∴ in right - angled AXS and AYX.
we get , XS = YS [ ∵ S is the mid - point of XY.
∴∠ASX=∠ASY[∵ each is right angle .
and AS in common to both .
∴ΔAXS~=ΔAYS,∴XA=YA[∵ similar sides of two congrument triangles ]
Now , XY XY, and PQ are both perpendiculars to PQ.
∴XY∣∣PQ
Again ∵ XM and YN are both perpendicula r to Pq .
∴XM=YM
Now in ΔAXMandΔAYN,XY=YA,SX=SY and SA is common to both
∴ΔAXM≅ΔAYM [ by the S-S -S condition of congruent of congruency]
∴ AM = AN [∵similar sides of congruent triangles ]
or12PA=12AQ [ from (1) and (2)]
orPA=AQ,∴PA=AQ

Topper's Solved these Questions
- THEOREMS RELATED TO CIRCLE BOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO CIRCLE EXERCISE - Example (B. Write true or false )
3 Videos
- THEOREMS RELATED TO CIRCLE BOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO CIRCLE EXERCISE - Example (C. Fill in the blanks
2 Videos
- THEOREMS RELATED TO CIRCLE BOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO CIRCLE EXERCISE - Example (Short-Answer Type Questions)
5 Videos
- SPHEREBOOK - CALCUTTA BOOK HOUSECHAPTER - SPHEREEXERCISE - EXERCISE
36 Videos
- THEOREMS RELATED TO CYCLIC QUADRILATERAL BOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO CYCLIC QUADRILATERAL EXERCISE - Long -answer type questions (L.A.)
12 Videos
Similar Questions
Only one circle can be throught three collinear points .
View SolutionIf the ratio of length of two chords PQ and RS of the circle with centre at O be 1 : 1 then ∠POQ:∠ROS = _________.
View SolutionTwo equal circles of radius 10 cm intersect each other and the length of their common chord is 12 cm . Find the distance between the centre of the circle .
View SolutionIf the volume of a solid hemisphere be 19404 cc, then the radius of the hemisphere will be
View SolutionIn a cyclic quadrilateral, the ratio of three consecutive angle is 1 : 2 : 3 Find the value of first and third angles.
View SolutionTwo circles intersect each other at the points P and Q. Two straight lines through P and Q intersect one circle at the points A and C and the other circle at B and D. Prove the AC|| BD
View SolutionP(a,5a) and Q(4a,a) are two points. Two circles are drawn through these points touching the axis of y.
Centre of these circles are at
View Solutionदो समान वृत्त एक-दूसरे को बिन्दुओं A और B पर काटते हैं | A से होकर जाने वाली एक वृत्तों को P और Q बिन्दुओं पर मिलती है | सिद्ध कीजिए कि BP = BQ.
View SolutionTwo circles intersect each other at point P and Q. Secants drawn through p and Q intersect the circles at points A,B and D,C
Prove that :∠ADC+∠BCD=180∘
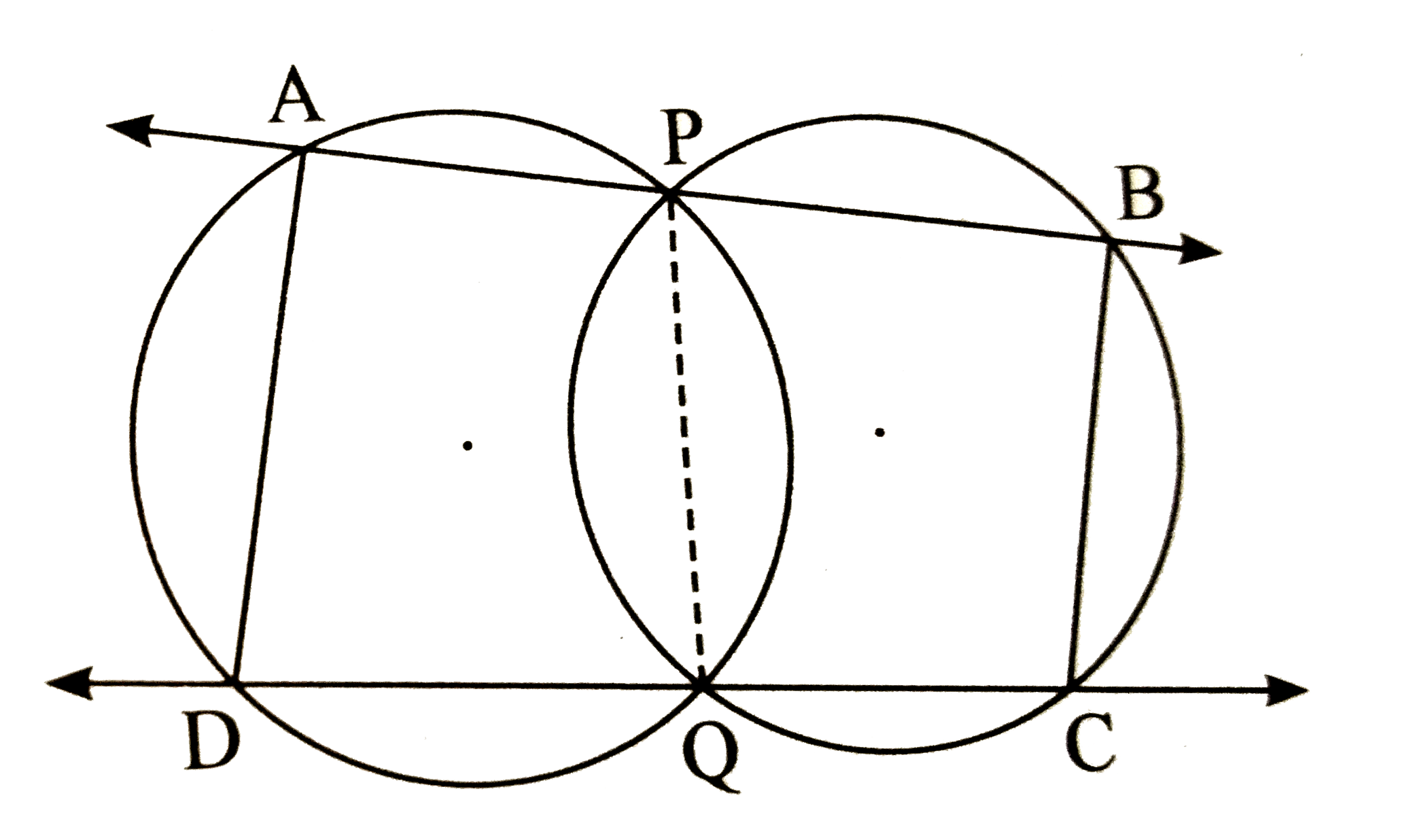
View SolutionThe centre of two circle are P and Q they intersect at the points A and B. The straight line parallel to the line segment PQ through the point A intersects the two circles at the point C and D Prove that CD=2PQ
View SolutionTwo circles intersect each other at the points P and Q. Two straight lines through P and Q intersect on circle at the points A and C and the other circle at B and D . Prove that AC||BD.
View SolutionTwo circles intersect each other at the points G and H . A straight line is drawn through the point G which intersect two circles at the points P and Q and the straight line through the point H parallel to PQ intersects the two circles at the points R and S . Prove that PQ=RS .
View SolutionIn two circles , one circle passes through the centre O of the other circle and they intersect each other at the points A and B . A straight line passing through A intersect the circle passing through O at the point P and the circle with centre at O at the point R . BY joining P , B and R , B prove that PR= PB.
View SolutionP is any point on diameter of a circle with centre O.A perpendicular drawn on diameter at the point O intersects the point O intersects the circle at the point Q. Extended QP intersects the circle at the point R.A tangent drawn at the point R intersects extended OP at the point S. Prove theat SP=SR.[GP−X]
View SolutionTwo chords AC and BD of a circle intersect each other at the point O. If two tangents drawn at the points A and B intersect each other at the point P and two tangents drawn at the points C and D intersect at the point Q, prove that ∠P+∠Q=2∠BOC.[GP−X]
View Solution
