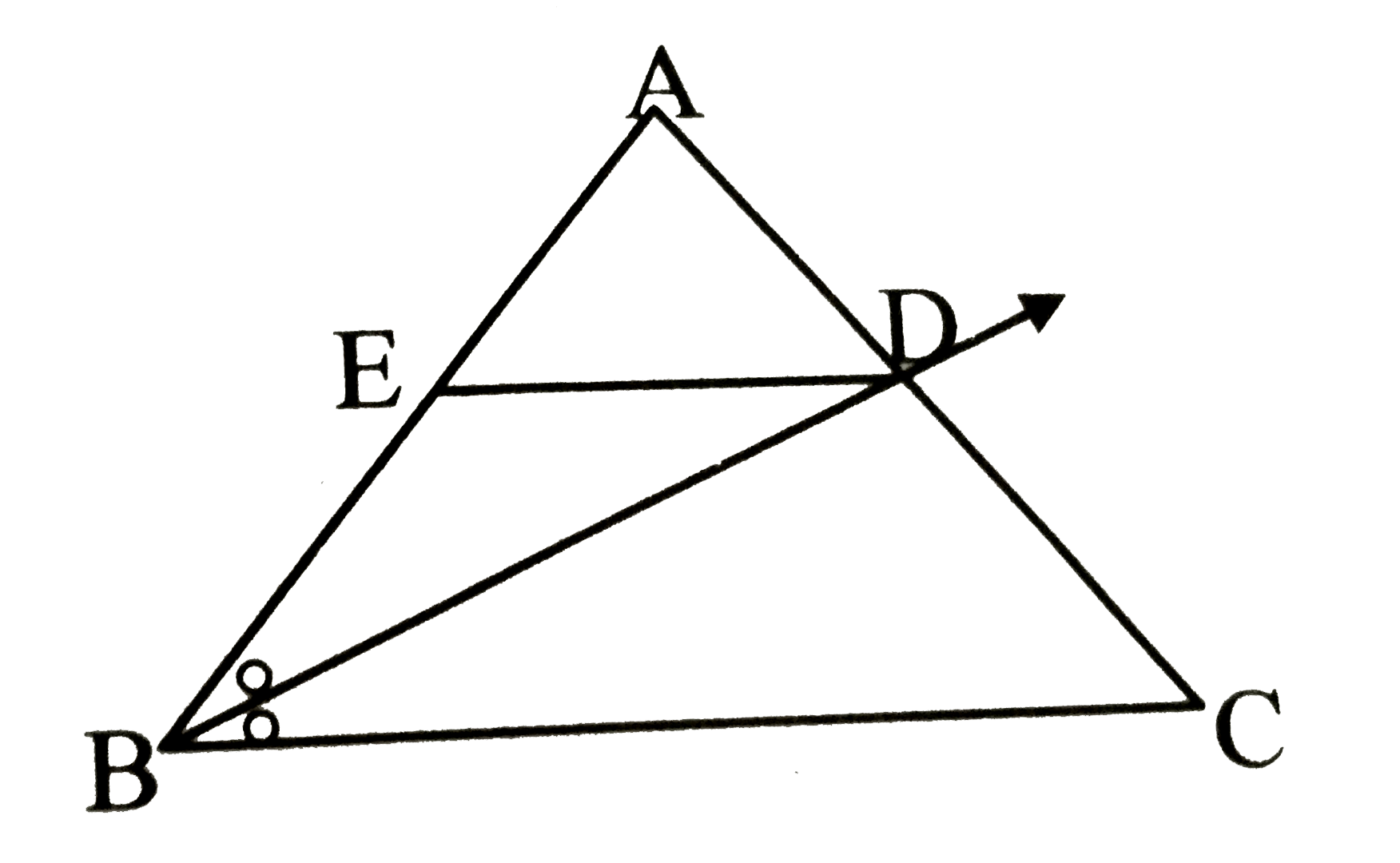
In ΔABC, ray BD bisects ∠ABC. A−D−C, side DE∣∣ side BC, A−E−B.
Prove that, ABBC=AEEB.
Complete the activity by filling the boxes.
![In DeltaABC, ray BD bisects /ABC. A-D-C, side DE|| side BC, A-E-B. Prove that, (AB)/(BC)=(AE)/(EB). Complete the activity by filling the boxes. In DeltaABC, ray BD is the bisector of /ABC :.(AB)/(BC)=square.......(I) (By angle bisector theorem) In DeltaABC, seg DE|| side BC :.(AE)/(EB)=(AD)/(DC)........(II) square :.(AB)/(square)=(square)/(EB).......[From (I) and (II)]](https://d10lpgp6xz60nq.cloudfront.net/physics_images/NVT_21_MAT_P2_X_C02_E01_017_Q01.png)
In ΔABC, ray BD is the bisector of ∠ABC
∴ABBC=□.......(I) (By angle bisector theorem)
In ΔABC, seg DE∣∣ side BC
∴AEEB=ADDC........(II) □
∴AB□=□EB.......[From (I) and (II)]
Video Solution
Text Solution
ADDC,ByBasic∝ortionalitytheorem,ABBC=AEEB
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
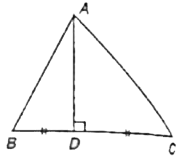
In the adjoning figure of ΔABC,AD is the perpendicular bisector of side BC. The triangle ABC is :
 Aright angledBisoscelesCscaleneDequilateral
Aright angledBisoscelesCscaleneDequilateral
In ΔABC, D is the midpoint of side AB. Line DE∣∣ side BC. A−E−C. Prove that pont E is the midpoint of side AC.
View SolutionIn ΔABC,ray BD bisects ∠ABC and ray CE bisects ∠ACB. If seg AB ≅seg AC, then prove that ED || BC.
View SolutionIn ΔABC, seg BD bisects ∠ABC. If AB=x, BC=x+5, AD=x−2, DC=x+2. Find the value of x.
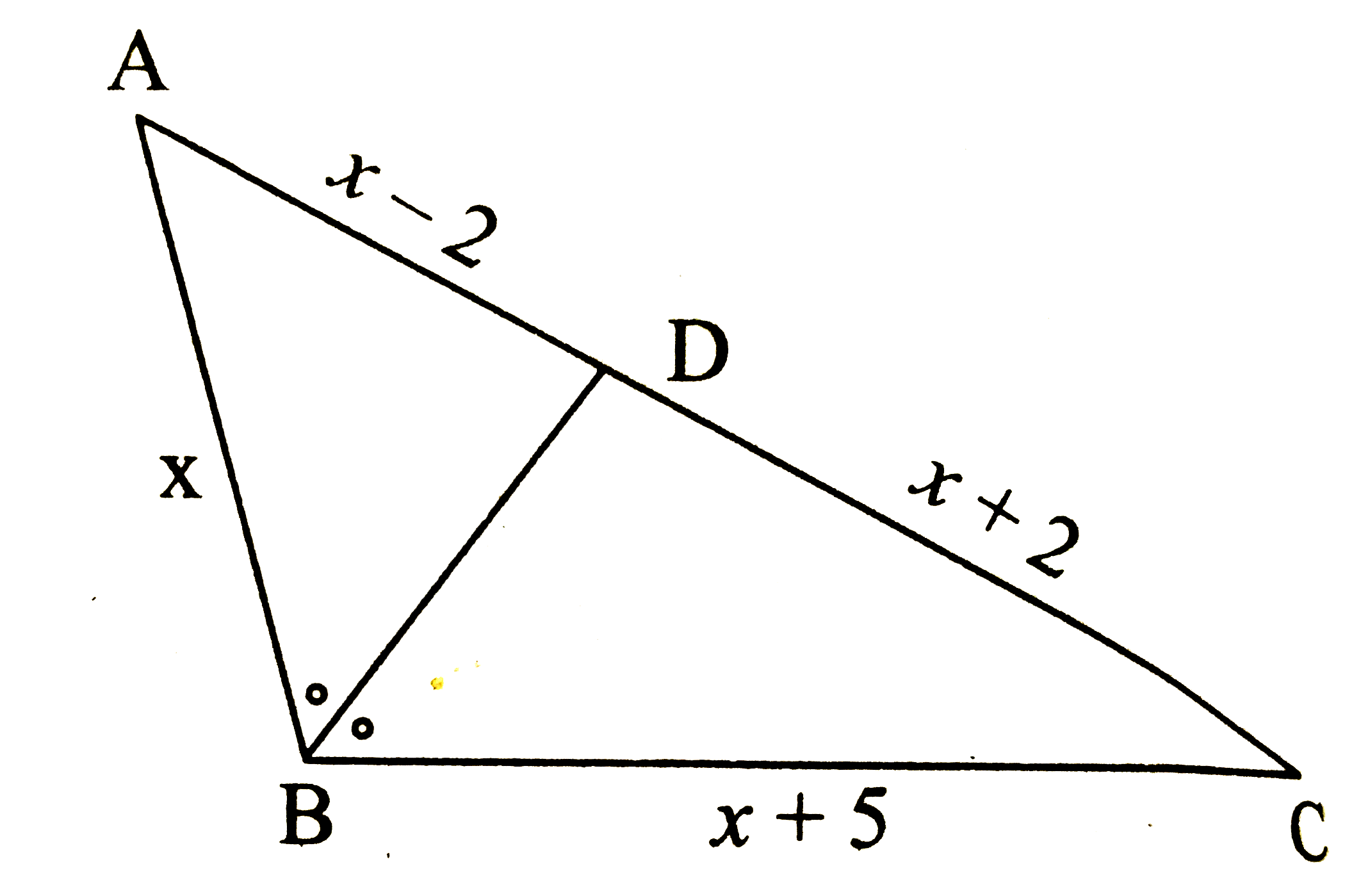
View SolutionIn ΔABC set BD bisects ∠ABC. If AB−x,BC=x+5,AD=x−2,DC=x+2, then find the value of x.

View SolutionIn ΔABC, seg DE∣∣ side BC. If 2Ar(ΔADE)=Ar(□DBCE), find AB:AD and show BC=√3×DE.
View SolutionIn ΔABC,D is any point on side BC. Prove that
AB+BC+CA>2AD
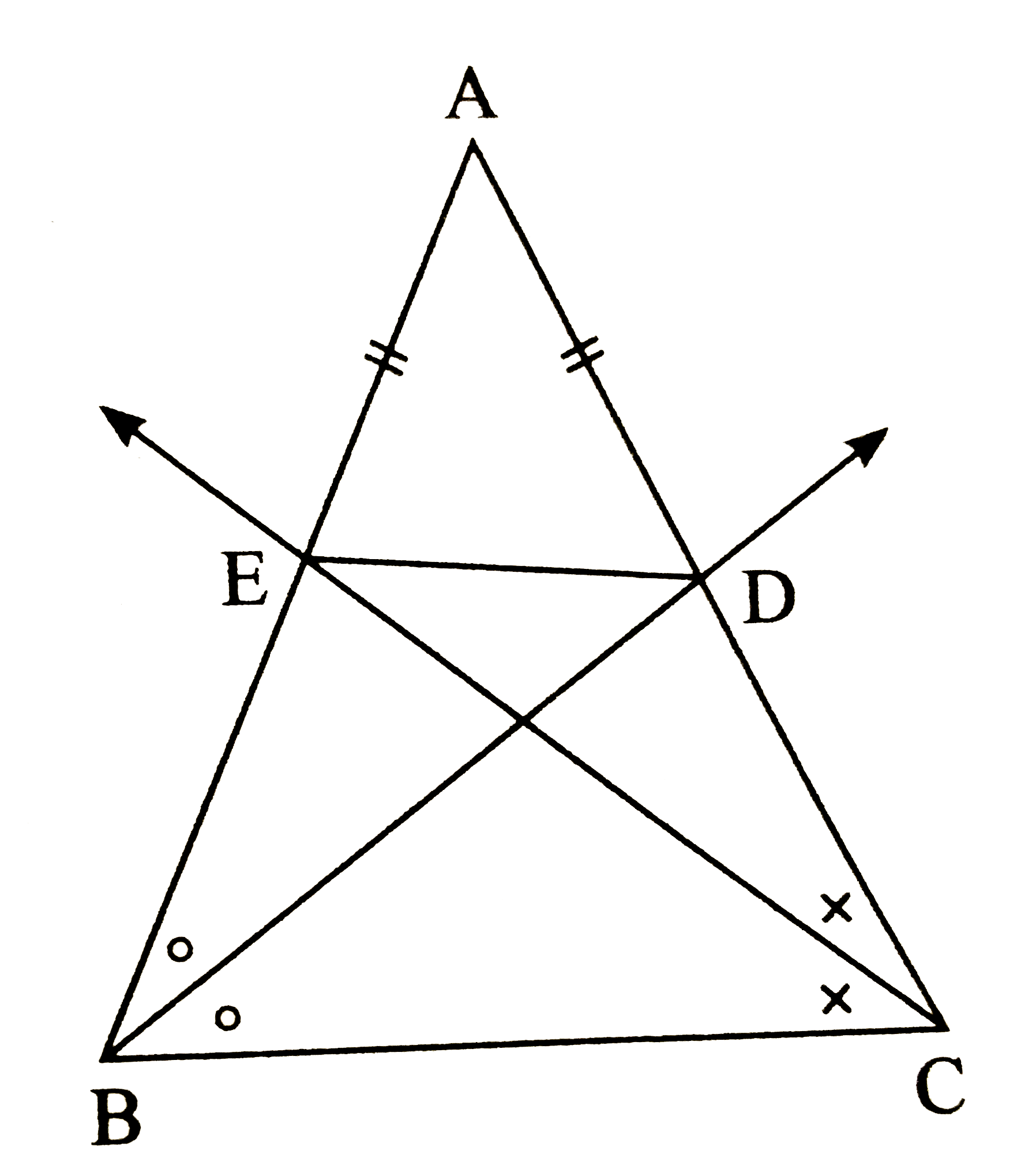
View SolutionIn the figure, seg AB≅ seg AC, ray CE bisects ∠ACB , ray BD bisects ∠ABC. Prove that ray ED∣∣ side BC.
View Solution