The relation between atomic radius and edge length 'a' of a body centred cubic unit cell :
A
r=a/2
B
r=√a/2
C
r=√34a
D
r=3a2
Video Solution
Text Solution
The correct Answer is:C
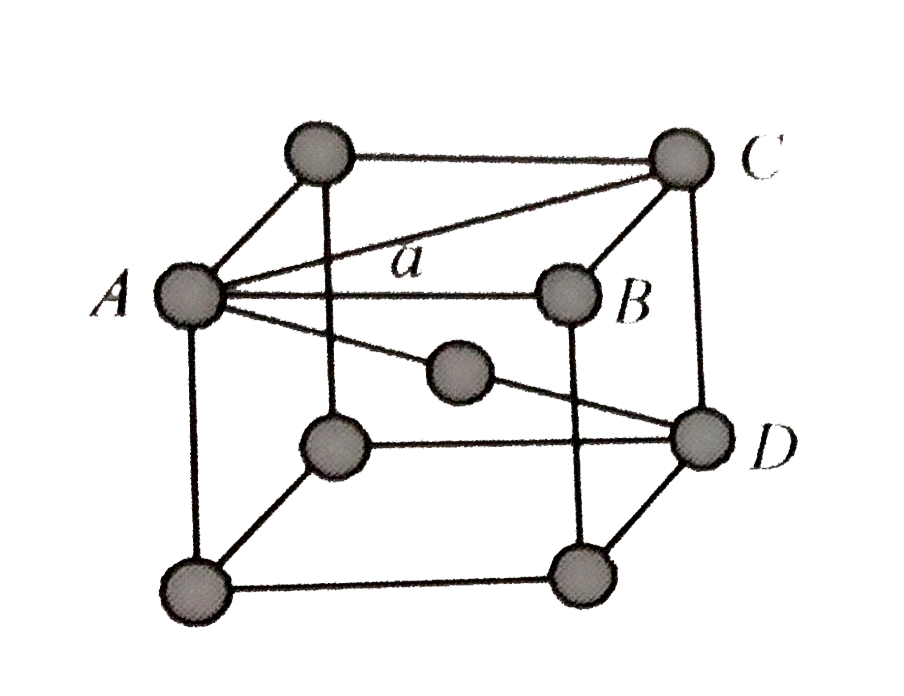
Distance between nearest neighbours, d=AD2
In right angled △ABC,AC2=AB2+BC2
AC2=a2+a2 or AC=√2a
Now in right angled △ADC,
AD2=AC2+DC2
AD2=(√2a)2+a2=3a2⇒AD=√3a
∴d=√3a2
Radius , r=d2=√34 a
|
Topper's Solved these Questions
- THE SOLID STATE BOOK - NCERT FINGERTIPSCHAPTER - THE SOLID STATE EXERCISE - Calculations Involving Unit Cell Dimensions
9 Videos
- THE SOLID STATE BOOK - NCERT FINGERTIPSCHAPTER - THE SOLID STATE EXERCISE - Imperfections In Solids
18 Videos
- THE SOLID STATE BOOK - NCERT FINGERTIPSCHAPTER - THE SOLID STATE EXERCISE - Number Of Atoms In Unit Cell And Close Packed Structures
29 Videos
- THE P-BLOCK ELEMENTS BOOK - NCERT FINGERTIPSCHAPTER - THE P-BLOCK ELEMENTS EXERCISE - Assertion And Reason
15 Videos
Similar Questions
Knowledge Check
The relation between atomic radius ( r ) and edge length ( a ) a face - centred cubic cell is
Ar=a2Br=a2√2Cr=a√34D√2a2In a close packed centred cubic lattice of potassium the corrcet relation between the atomic radius (r) of potassium and the edge length (a) of the cube is
Ar=a√2Br=a√3Cr=√32aDr=√34aThe coordination number of each atom in body centered cubic unit cell is
A(0,0,0) and (1/2,0,0)B(0,0,0) and (1/2,1/2, 1/2)C(0,0,0) and (0,1/2,0)D(0,0,0) and (0,0,1/2)
The radius of the largest shpere which fits properly at the centre of the edge of a body centred cubic unit cell is : (Edge length is represented by 'a')
View SolutionIn face centred cubic unit cell edge length is
View SolutionIn face centred cubic unit cell edge length is
View SolutionIn face centred cubic unit cell edge length is
View SolutionIn the face centred cubic unit cell, edge length is
View Solution
