Assertion : The amplitude of oscillation can never be infinite. lt brgt Reason : The energy of oscillator is continuously dissipated.
If both assertion and reson are true and reason is the correct explanation of assertion
If both assertion and reason are true but reason is not the correct explanation of assertion.
If assertion is true but reason is false.
If both assertion and reason are false.
The correct Answer is:A
A=F0/m√(ω2−ω20)2+(bω/m)2
From above equation, amplitude of oscillation, in absence of damping force (b=0), that the steady state amplitude approaches infinity as ω→ω0. That is, if there is not resistive force in the system and then it is possible to drive an oscillator with sinusoidal force at the resonance frequency, the amplitude of motion will build up without limit. this does not occur in practice because some damping is always present in real oscillation. due to presence of various dissipative force in the system, the amplitude of oscillation can grow to a large value only but cann never be infinite
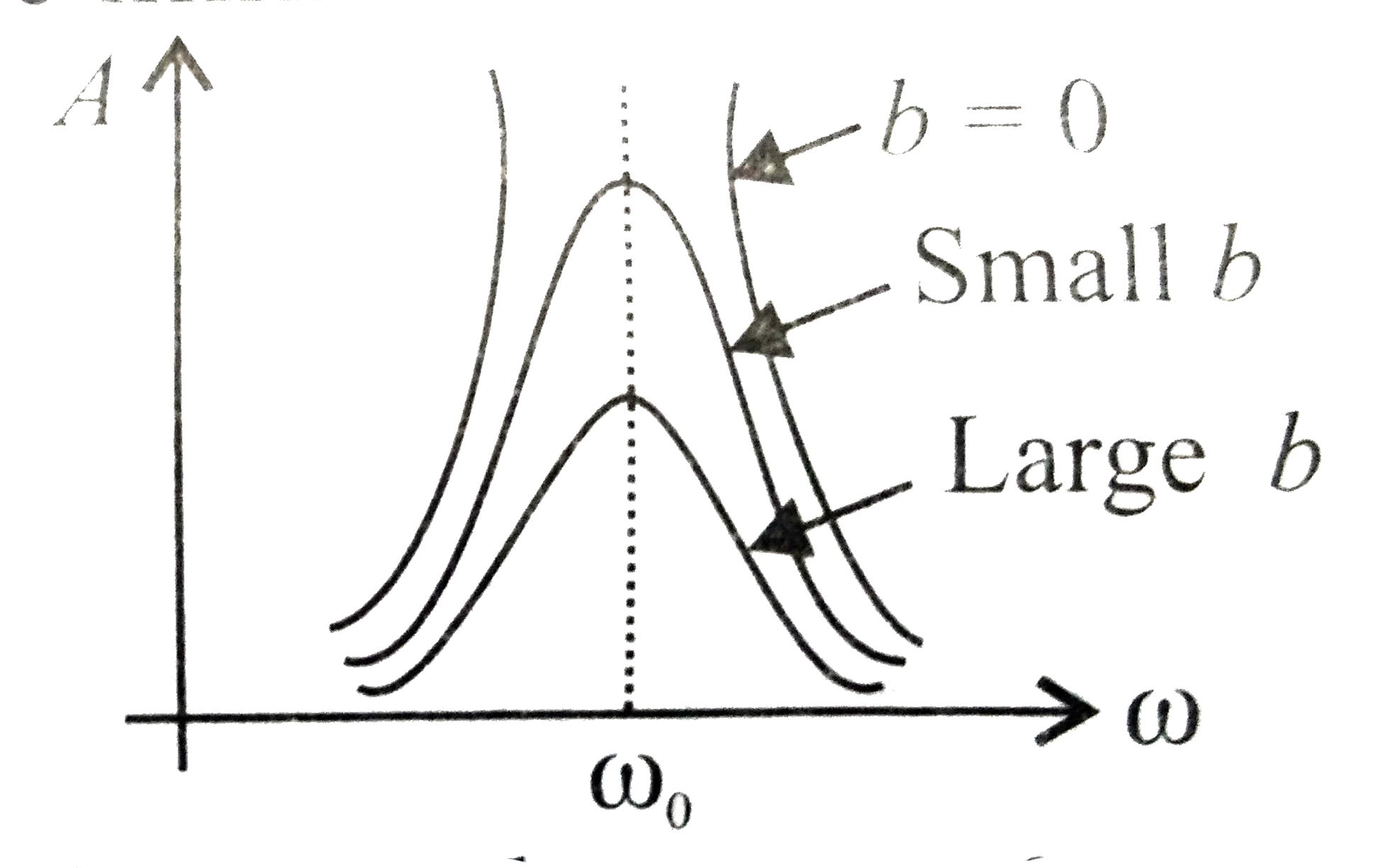
The graph showing amplitude as function of frequency for the forced oscillator with varying resistive force.
Topper's Solved these Questions
- OSCILLATIONS Book:NCERT FINGERTIPSChapter:OSCILLATIONS Exercise:Exemplar Problems
Explore 1 Video
- MOTION IN A STRAIGHT LINEBook:NCERT FINGERTIPSChapter:MOTION IN A STRAIGHT LINEExercise:Assertion And Reason
Explore 15 Videos
- PHYSICAL WORLDBook:NCERT FINGERTIPSChapter:PHYSICAL WORLDExercise:Assertion And Reason
Explore 10 Videos
Similar Questions
In dampled oscillations, the amplitude of oscillation is reduced to one-third of its initial value of 9cm at the end of 100 oscillations. What will be its amplitude of oscillation in cm when it completes 200 oscillations.
View SolutionIn dampled oscillations, the amplitude of oscillatinos is reduced to one-fourth of its initial value 10cm at the end of 50 oscillations. What will be its amplitude when the oscillator completes 150 oscillations ?
View Solution
Knowledge Check
At resonance the amplitude of forced oscillations is
AminimumBmaximumCzeroDNone of theseAt resonance, the amplitude of forced oscillations is
AminimumBmaximumCzeroDnone of theseVibrations, whose amplitudes of oscillations decrease with time, are called
Afree vibrationsBforced vibrationsCdamped vibrationsDnone of these
The kinetic energy of a particle executing SHM is 16J. When it is in its mean position. If the amplitude of oscillation is 25cm and the mass of the particle is 5.12 kg, the itme period of its oscillation in second is
View SolutionAssertion : The amplitude of an oscillation pendulum decreases gradually with time
Reason : The frequency of the pendulum decrease with time
View SolutionAssertion : In x-=3+4 cosωt , amplitude of oscillation is 4 units.
Reason : Mean position is at x=3.
View SolutionAssertion : For an oscillating simple pendulum, the tension in the string is maximum at the mean position and minimum at the extreme position. lt brgt Reason : The velocity of oscillating bob in simple harmonic motion is maximum at the mean position.
View SolutionAssertion: If the amplitude of a simple harmonic oscillator is doubled, its total energy becomes double.
Reason: The toal energy is directly proportional to the amplitude of vibration of the harmonic oscillator.
View Solution

