A mass attached to a spring is free to oscillate, with angular velocity ω, in a horizontal plane without friction or damping. It is pulled to a distance x0 and pushed towards the centre with a velocity v0 at time t=0. Determine the amplitude of the resulting oscillations in terms of the parameters ω,x0andv0.
√v20ω2−x20
√ω2v20+x20
√x20ω2+v20
√v20ω2+x20
The correct Answer is:D
Let the displacement of the block at instant of
time t be, x=Acos(ωt+ϕ)
At t=0,x=x0
∴x0=Acosϕ . . . (i)
Velocity, v=dxdt=−Aωsin(ωt+ϕ)
At t=0,v=−v0
∴−v0=−Aωsinϕ
or Asinϕ=v0ω
Squaring and adding (i) and (ii), we get
A2(sin2ϕ+cos2ϕ)=v20ω2+x20
A=√v20ω2+x20
Topper's Solved these Questions
- OSCILLATIONS Book:NCERT FINGERTIPSChapter:OSCILLATIONS Exercise:Force Law For Simple Harmonic Motion
Explore 2 Videos
- OSCILLATIONS Book:NCERT FINGERTIPSChapter:OSCILLATIONS Exercise:Energy In Simple Harmonic Motion
Explore 11 Videos
- OSCILLATIONS Book:NCERT FINGERTIPSChapter:OSCILLATIONS Exercise:Simple Harmonic Motion And Uniform Circular Motion
Explore 3 Videos
- MOTION IN A STRAIGHT LINEBook:NCERT FINGERTIPSChapter:MOTION IN A STRAIGHT LINEExercise:Assertion And Reason
Explore 15 Videos
- PHYSICAL WORLDBook:NCERT FINGERTIPSChapter:PHYSICAL WORLDExercise:Assertion And Reason
Explore 10 Videos
Similar Questions
Knowledge Check
A mass attached to a string rotates about a fixed centre with an angular velocity ω in a horizontal plane ,The length of the string and the angular velocity are now doubled .IF T0 is the initial tension in the string , then the new tension will be
A2T0B4T0C8T0D6T0A solid sphere with a velocity (of centre of mass) v and angular velocity ω is gently placed on a rough horizontal surface. The frictional force on the sphere :
Amust be forward (in direction of v)Bmust be backward (opposite to v)Ccannot be zeroDnone of the aboveA block of mass m is pushed towards the movable wedge of mass M and height h, with a velocity v0. All surfaces are smooth . The minimum value of v0 for which the block will reach the top of the wedge is
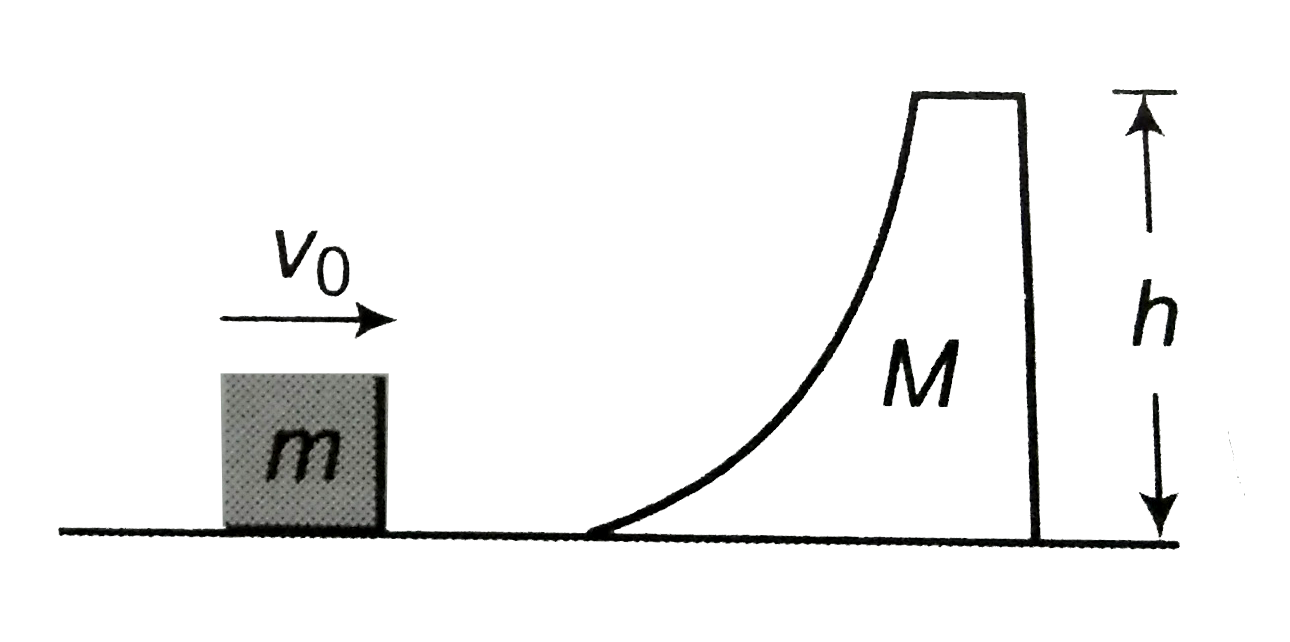 A√2ghB√2ghmMC√2gh(m+M)MD√2ghm(m+M)
A√2ghB√2ghmMC√2gh(m+M)MD√2ghm(m+M)
Find the angular frequency and the amplitude of harmonic oscillations of a particle if at distances x1 and x2 from the equalibrium position its velocity equald v1 and v2 respectively.
View SolutionA block of mass 1 kg attached to a spring is made to oscillate with an initial amplitude of 12 cm. After 2 minutes the amplitude decreases to 6 cm. Determine the value of the damping constant for this motion. (take In 2 =0.693 )
View SolutionA mass M attached to a spring of spring constant 0.7 N/m oscillates on a smooth horizontal table. When displacement is 0.3 m, velocity is 2 ms−1. And when displacement is 0.4 m, velocity is 0.3 m/s. Calculate the vlaue of M.
View SolutionA uniform solid sphere of radius R, rolling without sliding on a horizontal surface with an angular velocity ω0, meets a rough inclined plane of inclination θ=60∘. The sphere starts pure rolling up the plane with an angular velocity ω Find the value of ω.

View SolutionA billiard ball of mass m and radius r, when hit in a horizontal direction by a cue at a height h above its centre, acquired a linear velocity v0. The angular velocity ω0 acquired by the ball is
View Solution