A sperical capacitor consists of two concentric spherical conductors, held in position by suitable insulating supports. Show that the capacitance of this spherical capacitor is given by C=4π∈0r1r2r1−r2,
Where r1andr2 are radill of outer and inner spheres respectively.
4πε0r1r2r1−r2
4πε0−(r2−r1)r1r2
r1r24πε0(r2−r1)
(r1−r2)4πε0r1r2
The correct Answer is:A
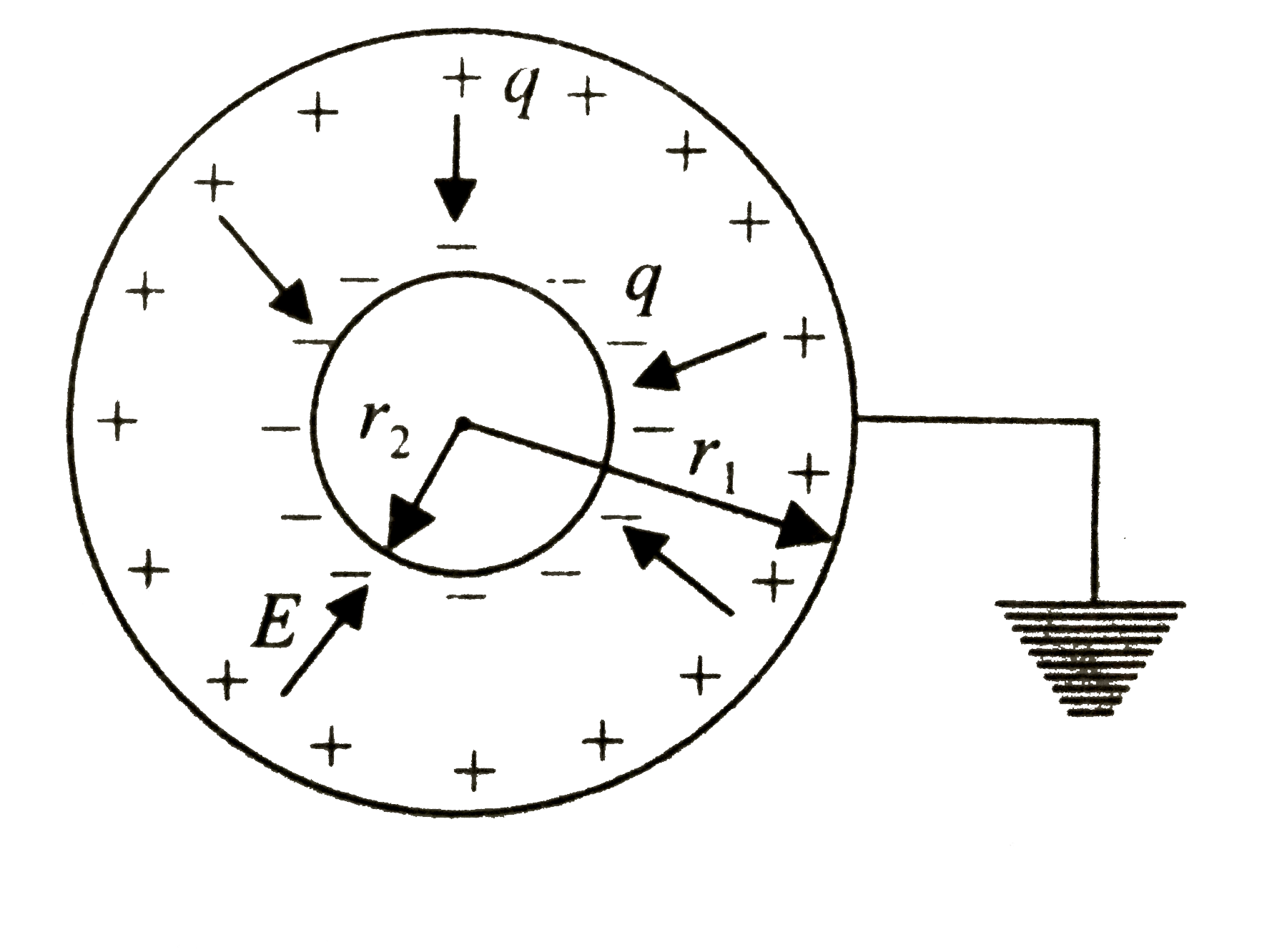
As show in figure , +q charge spreads uniformly on inner surface of outer sphere of radius r1. The iduced charge −q spreads uniformly on the outer surface of inner sphere of radius r2 .
The outer surface of outer sphere is earthed. Due to electrostatic shielding .
E=0 for r<r2 and E=0 for r<r1 .
In the space between the two sphere, Potential difference between two spheres,
V=q4πε0r2−q4πε0r1=q4πε0[1r2−1r1]
V=q4πε0(r1−r2r1r2)
Also c=qV
∴C=4πε0r1r2r1−r2 (using (i))
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCE Book:NCERT FINGERTIPSChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCE Exercise:The Parallel Plate Capacitor
Explore 5 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE Book:NCERT FINGERTIPSChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCE Exercise:Effect Of Dielectric On Capacitance
Explore 6 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE Book:NCERT FINGERTIPSChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCE Exercise:Dielectrics And Polarisation
Explore 4 Videos
- ELECTROMAGNETIC WAVESBook:NCERT FINGERTIPSChapter:ELECTROMAGNETIC WAVESExercise:Assertion And Reason
Explore 15 Videos
- MAGNETISM AND MATTER Book:NCERT FINGERTIPSChapter:MAGNETISM AND MATTER Exercise:Assertion And Reason
Explore 15 Videos
Similar Questions
Knowledge Check
The capacitance of two concentric spherical shells of radii R1 and R2(R2>R1) is
A4πε0R2B4πε0(R2−R1)R1R2C4πε0R1R2(R2−R1)D4πε0R1A spherical capacitor consists of two concentric spherical conductors , the inner one of radius R1 maintained at potential V1 and the outer conductor of radius R2 at potential V2 . The potential at a point P at a distance x from the centre (where R2>x>R1) is
A(V1−V2)(x−R1)(R2−R1)BV1+V2x(R2−R1)CV1R1(R2−x)+V2R2(x−R1)(R2−R1)xD(V1+V2)(R1+R2)x
show that r2r3+r3r1+r1r2=s2
View Solution1 If r and R be the radii of inner and outer circles respectively, then area of ring is
View SolutionThree concentric spherical conductors A, B and C of radii R, 2R and 4R respectively. A and C is shorted and B is uniformly charged
Potential at A is

View SolutionThree concentric spherical conductors A, B and C of radii R, 2R and 4R respectively. A and C is shorted and B is uniformly charged .
Potential at B is

View SolutionProve that r1r2+r2r3+r3r1=14(a+b+c)2
View SolutionThree concentric spherical conductors A, B and C of radii R, 2R and 4R respectively. A and C is shorted and B is uniformly charged
Charge on conductor A is

View Solution