Two insulated charged metallic spheres P and Q have their centres separated by a distance of 60 cm. The radii of P and Q are negligible compared to the distance of separation. The mutual force of electrostatic repulsion if the charge on each is 3.2×10−7C is
5.2×10−4N
2.5×10−3N
1.5×10−3N
3.5×10−4N
The correct Answer is:B
To solve the problem of finding the mutual force of electrostatic repulsion between two charged metallic spheres P and Q, we can use Coulomb's Law. Here’s the step-by-step solution:
Step 1: Understand the given data
- Distance between the centers of the spheres (r) = 60 cm = 0.6 m (conversion from cm to m)
- Charge on each sphere (q1 and q2) = 3.2×10−7C
Step 2: Write down Coulomb's Law
Coulomb's Law states that the electrostatic force (F) between two point charges is given by the formula:
F=14πϵ0⋅q1⋅q2r2
where:
- F = electrostatic force between the charges,
- q1 and q2 = magnitudes of the charges,
- r = distance between the centers of the charges,
- ϵ0 = permittivity of free space = 8.85×10−12C2/(N⋅m2).
Step 3: Substitute the values into the formula
Since both spheres have the same charge, we can set q1=q2=q=3.2×10−7C. Thus, we can rewrite the formula as:
F=14πϵ0⋅q2r2
Substituting the known values:
F=14π(8.85×10−12)⋅(3.2×10−7)2(0.6)2
Step 4: Calculate q2 and r2
Calculate q2:
q2=(3.2×10−7)2=1.024×10−13C2
Calculate r2:
r2=(0.6)2=0.36m2
Step 5: Substitute these values into the formula
Now substitute q2 and r2 into the force equation:
F=14π(8.85×10−12)⋅1.024×10−130.36
Step 6: Calculate the force
First, calculate the denominator:
4π(8.85×10−12)≈1.11265×10−10
Now calculate:
F=1.024×10−130.36≈2.8444×10−13
Finally, calculate the force:
F≈2.8444×10−131.11265×10−10≈2.55×10−3N
Final Answer
The mutual force of electrostatic repulsion between the two spheres is approximately 2.55×10−3N.
- Distance between the centers of the spheres (r) = 60 cm = 0.6 m (conversion from cm to m)
- Charge on each sphere (q1 and q2) = 3.2×10−7C
Coulomb's Law states that the electrostatic force (F) between two point charges is given by the formula:
F=14πϵ0⋅q1⋅q2r2
where:
- F = electrostatic force between the charges,
- q1 and q2 = magnitudes of the charges,
- r = distance between the centers of the charges,
- ϵ0 = permittivity of free space = 8.85×10−12C2/(N⋅m2).
Since both spheres have the same charge, we can set q1=q2=q=3.2×10−7C. Thus, we can rewrite the formula as:
F=14πϵ0⋅q2r2
F=14π(8.85×10−12)⋅(3.2×10−7)2(0.6)2
Calculate q2:
q2=(3.2×10−7)2=1.024×10−13C2
Calculate r2:
r2=(0.6)2=0.36m2
Now substitute q2 and r2 into the force equation:
F=14π(8.85×10−12)⋅1.024×10−130.36
First, calculate the denominator:
4π(8.85×10−12)≈1.11265×10−10
Now calculate:
F=1.024×10−130.36≈2.8444×10−13
Finally, calculate the force:
F≈2.8444×10−131.11265×10−10≈2.55×10−3N
The mutual force of electrostatic repulsion between the two spheres is approximately 2.55×10−3N.
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDSBOOK - NCERT FINGERTIPSCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Force Between Multiple Charges
5 Videos
- ELECTRIC CHARGES AND FIELDSBOOK - NCERT FINGERTIPSCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Electric Field
16 Videos
- ELECTRIC CHARGES AND FIELDSBOOK - NCERT FINGERTIPSCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Basic Properties Of Electric Charge
7 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - NCERT FINGERTIPSCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - Assertion And Reason
15 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - NCERT FINGERTIPSCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Assertion And Reason
15 Videos
Similar Questions
Two insulated charged copper spheres A and B have their centress separated by a distance of 50 cm . What is the mutual force of electrostatic repulsion if the charges on each is 6.5×10−7C ? The radii of A and B are neglible compared to the distance of separation
(b) What is the force of repulsion if each sphere is charged bouble the above amount, and the distance between them is halved?
View Solution(a) Two insulated charged copper spheres A and B have their centers speparated by a distance of 50 cm. What is the mutal force of electrostatic repulsion if the charge on each is 6.5×10−7C ? The radill of A and B are negalible compared to the distance of separation.
(b) What is the force of repulsion if each sphere is charged double the above amount, and the distance between them is halved ?
View Solution
Knowledge Check
Two insulated charged copper spheres A and B have their centres separated by a distance of 50 cm. The charge on each spheres is 6.5×10−7C.The radii of A and B are negligible compared to their separation. If each sphere is charged double the above amount, and the distance between them is halved. Then, what is the ratio of force between spheres in two cases?
A12B14C18D116Two point charges Q and −Q/4 are separated by a distance X. Then
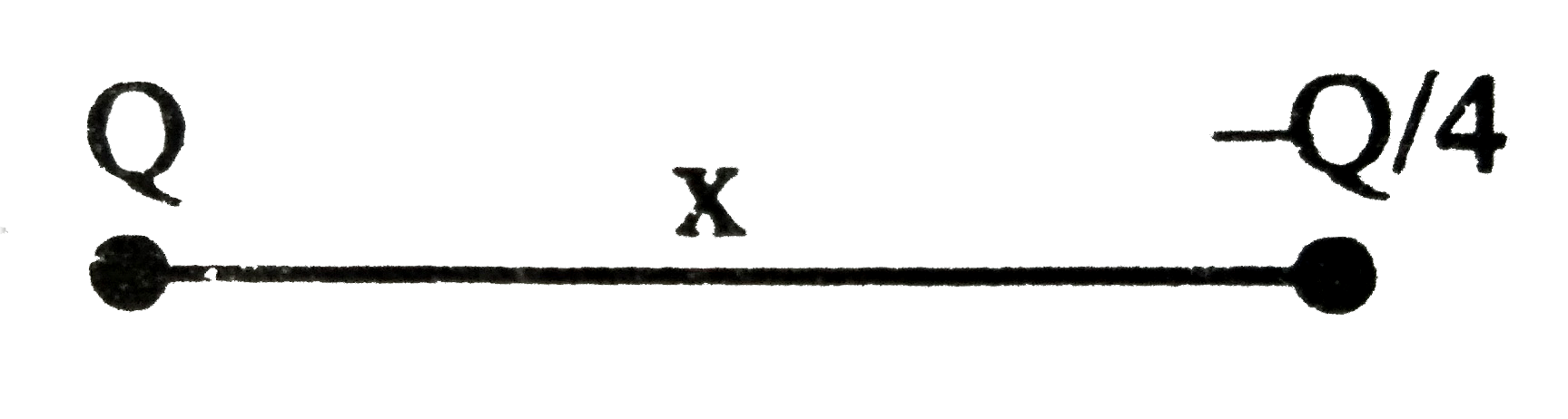.Apotential is zero at a point on the axis which is x/3 on the right side of the cahrge −q/4Bpotential is zero at a point on the axis which is x/5 on the left side fo the charge −Q/4Celectric field is zero at a point on the axis which is at a distance x on the right side fo the charge −Q/4Dthere exist two points on the axis where electric field is zero.Two conducting spheres of radii 3 cm and 1 m are separated by a distance of 10 cm in free space. If the spheres are charged to same potential of 10 V each, then the force of repulsion between them is
A(13)×10−9NB(29)×10−9NC(19)×10−9ND(49)×10−9N
Find the minimum electrostatic force that can exist between two charges separated by distance 1m.
View SolutionTwo charges q and 3q are placed fixed on x-axis separated by distance 'd'. Where should a third charge 2q be placed such that it will not experience any force ?
View SolutionTwo charges Q and -3Q are placed fixed on x-axis separated by a distance 'd' Where should a third charge 2Q be placed such that it will not experience any force?
View SolutionTwo insulated charged conducting spheres of radii 20cm and 15cm respectively and having an equal charge of 10C are connected by a copper wire and then they are separted. Then
View SolutionTwo charges q and −3q are placed fixed on x-axis separated by distance d. Where should a third charge 2q be placed such that it will not experience any force ?
View Solution