मान लीजिए की N में a∗b=a तथा b का HCF द्वारा परिभाषित एक द्विआधारी संक्रिया है। क्या ∗ क्रमविनिमेय है? क्या ∗ साहचर्य है ? क्या N में इस द्विआधारी संक्रिया के तत्समक का अस्तित्व है ?
यहाँ a∗b=a और b का HCF=∀a,b∈N
द्विआधारी संक्रिया ∗ की N में क्रमविनिमेयता एवं साहचर्यता उपरोक्त उदाहरण के अनुसार विद्यार्थी स्वयं हल करें।
तत्समक अवयव - माना N में तत्समक अवयव e है, तब,
a∗e=e∗a=a∀a∈N
⇒a और e का HCF=a और e और a का HCF=a
⇒ प्रत्येक a∈N के लिए a,e का भाजक है। [ जैसे HCF(2,4)=2]
अतः एक संख्या e इस प्रकार है की जो प्रत्येक a∈N से विभाजित होता है, जो की संभव नहीं है ।
Topper's Solved these Questions
- द्वी-आधारी संक्रियाएँBOOK - PRABODH PUBLICATIONCHAPTER - द्वी-आधारी संक्रियाएँEXERCISE - प्रश्नावली 3.1
25 Videos
- द्वी-आधारी संक्रियाएँBOOK - PRABODH PUBLICATIONCHAPTER - द्वी-आधारी संक्रियाएँEXERCISE - प्रश्नावली 3.2
9 Videos
- द्वितीय कोटि का अवकलज BOOK - PRABODH PUBLICATIONCHAPTER - द्वितीय कोटि का अवकलज EXERCISE - प्रश्नावली 12.1
31 Videos
- निश्चित समाकलन BOOK - PRABODH PUBLICATIONCHAPTER - निश्चित समाकलन EXERCISE - वस्तुनिष्ट प्रश्न
15 Videos
Similar Questions
N में a∗b=a+b2 द्वारा परिभाषित संक्रिया ∗
View Solutionपूर्णांक संख्याओं के समुच्चय Z में द्विआधारी संक्रिया ∗ इस प्रकार परिभाषित है की a∗b=a+b−4, जहाँ a,b∈Z (i) दर्शाइए की ∗ क्रमविनिमेय और साहचर्य होता है। (iii) Z में तत्समक अवयव ज्ञात कीजिए(iv) में व्युत्क्रम अवयव ज्ञात कीजिए।
View Solutionइन फलनों का द्वितीय कोटि के अवकलज ज्ञात कीजिये -
sin(logx)
View Solution∫baf(x)dx का मान है
View Solutionयदि संख्याएँ n-3,4n-2, तथा 5n+1 समांतर क्सेदी (AP) में हो, तो n का मान क्या है ?
View SolutionZ में a∗b =a-bद्वारा परिभाषित द्विआधारी संक्रिया*के लिए निर्धारित कीजिए कि क्या*द्विआधारी, क्रमविनिमेय तथा साहचर्य है ?
View Solutionएक द्विआधारी संख्या (cdccddcccddd)2 से निरूपित की जाती है, जहाँ c>d है । इसका दशमलव तुल्य क्या है ?
View Solutionएक द्विआधारी संक्रिया ∗Z+ पर निम्न रूप परिभाषित है :
a∗b=ab−bजहाँa,b∈Z+
2∗5 का मान ज्ञात कीजिए , जहाँ Z+ धनात्मक पूर्णांकों का समुच्चय है ।
View Solutionमान लीजिए कि R में द्वि -आधारी संक्रिया ∗,a∗b=1+ab,a,b∈R, तो संक्रिया ∗ :
(i) क्रम - विनिमेय है किन्तु साहचर्य नहीं है । , (ii) साहचर्य है किन्तु क्रम - विनिमेय नहीं है ।
(iii) न तो क्रम - विनिमेय है और न साहचर्य है । , (iv) क्रम - विनिमेय तथा साहचर्य दोनों ही है ।
View Solutionयदि परिमेय संख्याओं के समुच्चय Q पर संक्रिया (∗) इस प्रकार परिभाषित है कि a∗b=2a+3b . दिखाइए कि (∗) समुच्चय Q पर एक द्विआधारी संक्रिया है।
View Solutionयदि संक्रिया ∗ वास्तविक संख्याओं के समुच्चय R पर द्विआधारी संक्रिया है तथा इस प्रकार परिभाषित है कि
a∗b=√a4+b4 , जहाँ a,b∈R से दिखाइए कि '∗' क्रम-विनिमेय नियम का पालन करती है।
View Solutionयदि द्विआधारी संक्रिया ∗ वास्तविक संख्याओं के समुच्चय R पर इस प्रकार परिभाषित है कि
a∗b=ab2+1, जहाँ a,b∈R
तो द्विआधारी संक्रिया ∗ के साहचर्यता (associativity) की जाँच कीजिए।
View Solutionभौतिकी क्या है? || सिद्धांत तथा नियम में क्या अंतर है? || भौतिकी का प्रयोजन तथा उत्तेजना || प्रकृति में मूल बल || भौतिक नियमों की प्रकृति
View Solutionतथाकथित त्रिभुजीय संख्याएँ Tn लीजिये :
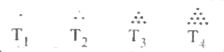
बिन्दुओ का विन्यास इस प्रकार किया गया है की इनसे एक त्रिभुज बनता है ।
यहाँ T1=1,T2=3,T3=6,T4=10 आदि आदि। क्या आप अनुमान लगा सकते है की T5 क्या है।
T6 के बारे में आप क्या कह सकते है ?
Tn के बारे में आप क्या कह सकते है ?
T8 का एक कंजेक्चर दीजिये।
View Solutionयदि संख्या 354Y2, 6 का एक गुणज है तो Yअंक का मान क्या हो सकता है?
View Solution'ये एहतियात जरूरी है इस बहर के लिए पंक्ति में 'बहर' का' अर्थ क्या है?
View Solution
