माना एक अरिक्त समुच्चय X के लिए एक द्विआधारी संक्रिया ∗:P(X)×P(X)→P(X),A∗B=A∩B∀,B∈P(X) द्वारा परिभाषित है, जहाँ P(X) समुच्चय X का घाट समुच्चय है।
(i) दर्शाइए की ∗ क्रमविनिमेय और साहचर्य है।
(ii) दर्शाइए की P(X) में केवल Xव्युत्क्रमणीय है।
यहाँ A∗B=A∩B∀,A,B∈P(X)
(i) उपरोक्त उदाहरण के अनुसार ।
(ii) तत्समक अवयव : चूँकि सभी A∈P(X) के लिए,
A⊂X
⇒A∩X=A=X∩A
⇒A∗X=A=X∗A∀A∈P(X)
अतः P(X) में ∗ के लिए X तत्समक अवयव है।
(iii) प्रतिलोम अवयव : माना P(X) में A व्युत्क्रमणीय है, तब एक अवयव B∈P(X) का अस्तित्व इस प्रकार है की:
A⋅B=X=B∗A
⇒A∩B=X और B∩A=X
⇒A=B=X [∴A⊂,XB⊂X]
अतः P(X) में केवल X व्युत्क्रमणीय है।
Topper's Solved these Questions
- BOOK - PRABODH PUBLICATIONCHAPTER - द्वी-आधारी संक्रियाएँEXERCISE - प्रश्नावली 3.125videos
द्वी-आधारी संक्रियाएँ
- BOOK - PRABODH PUBLICATIONCHAPTER - द्वी-आधारी संक्रियाएँEXERCISE - प्रश्नावली 3.29videos
द्वी-आधारी संक्रियाएँ
- BOOK - PRABODH PUBLICATIONCHAPTER - द्वितीय कोटि का अवकलज EXERCISE - प्रश्नावली 12.131videos
द्वितीय कोटि का अवकलज
- BOOK - PRABODH PUBLICATIONCHAPTER - निश्चित समाकलन EXERCISE - वस्तुनिष्ट प्रश्न15videos
निश्चित समाकलन
Similar Questions
N में a∗b=a+b2 द्वारा परिभाषित संक्रिया ∗
02:23View Solutionपूर्णांक संख्याओं के समुच्चय Z में द्विआधारी संक्रिया ∗ इस प्रकार परिभाषित है की a∗b=a+b−4, जहाँ a,b∈Z (i) दर्शाइए की ∗ क्रमविनिमेय और साहचर्य होता है। (iii) Z में तत्समक अवयव ज्ञात कीजिए(iv) में व्युत्क्रम अवयव ज्ञात कीजिए।
View Solutionइन फलनों का द्वितीय कोटि के अवकलज ज्ञात कीजिये -
sin(logx)View Solution∫baf(x)dx का मान है
05:23View Solutionनिम्निलिखित प्रतिचित्रण की एकेकी और आच्छादकता की जाँच कीजिए -
f:N→N जो f(x)=x2,x∈N से परिभषित है , N धन पूर्णाकों का समुच्चय है03:31View Solutionयदि X एक चर है कि P(X=1)=P(X=4) है तो P(X=4) का मान है-
01:11View Solutionअऋण (Non - negative ) संख्याओं के समुच्चय W पर संक्रियां * निम्न प्रकार परिभाषित है a ∗b=a^(b) सिद्ध कीजिए की * समुच्चय W पर द्विआधारी संक्रिया नहीं है|
02:42View Solutionकिसी प्रदत्त अतिरिक्त समुच्चक X के लिए ∗:P(X)×P(X)→P(X), माना ∗:P(X)×P(X)→P(X), जहाँ
A∗B=(A−B)∪(B−A)∀,B∈P(X)
द्वारा परिभाषित है। सिद्ध कीजिए की रिक्त समुच्चय ϕ संक्रिया, ∗ का तत्समक है तथा P(X) के समस्त अवयव A व्युत्क्रमणीय है।01:52View SolutionZ में a∗b =a-bद्वारा परिभाषित द्विआधारी संक्रिया*के लिए निर्धारित कीजिए कि क्या*द्विआधारी, क्रमविनिमेय तथा साहचर्य है ?
07:03View Solutionएक द्विआधारी संक्रिया ∗Z+ पर निम्न रूप परिभाषित है :
a∗b=ab−bजहाँa,b∈Z+
2∗5 का मान ज्ञात कीजिए , जहाँ Z+ धनात्मक पूर्णांकों का समुच्चय है ।05:22View Solutionयदि परिमेय संख्याओं के समुच्चय Q पर संक्रिया (∗) इस प्रकार परिभाषित है कि a∗b=2a+3b . दिखाइए कि (∗) समुच्चय Q पर एक द्विआधारी संक्रिया है।
02:36View Solutionयदि संक्रिया ∗ वास्तविक संख्याओं के समुच्चय R पर द्विआधारी संक्रिया है तथा इस प्रकार परिभाषित है कि
a∗b=√a4+b4 , जहाँ a,b∈R से दिखाइए कि '∗' क्रम-विनिमेय नियम का पालन करती है।02:17View Solutionएक याद्द्च्छिक चर X का प्रायिकता बंटन नीचे दिया गया है-
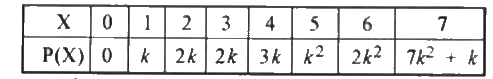ज्ञात कीजिये-
(i) k
(ii) P(X < 6)
(iii) P(X ge 6) (iv) P(0 < X <5)01:02View Solutionएक यादृच्छिक चर X मान 0,1,2,3 ग्रहण करता है | चर X का माध्य 1.3 है | यदि P(x=3)=2P(X=1) तथा P(X=2)=0.3 हो , तो P(X=0)है |
02:44View Solutionसमीकरण निकाय x+y=2π3,cosx+cosy=32, जहाँ x और y वास्तविक है , के हलों का समुच्चय ………….. है।
03:26View Solution