यदि एक त्रिभुज के शीर्ष कोण का समद्विभाजक सम्मुख भुजा को भी समद्विभाजित करता है तो सिद्ध कीजिए कि त्रिभुज एक समद्विबाहु त्रिभुज है ।
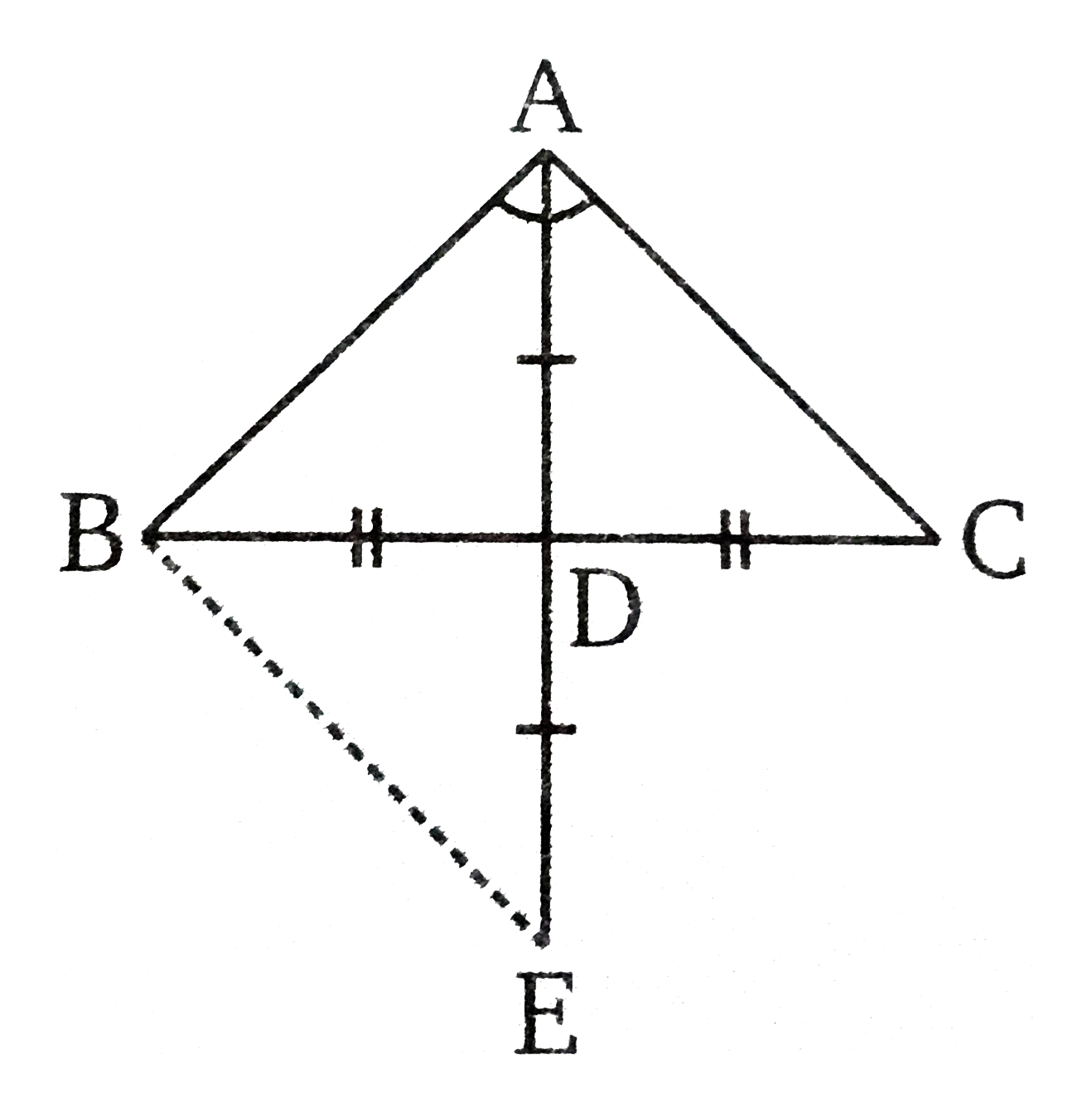
दिया है : एक त्रिभुज ABC है जिसमे शीर्ष ∠A का समद्विभाजक AD, BC पर D में इस प्रकार मिलता है कि BD = DC
सिद्ध करना है : AB = AC
रचना :AD को E तक इस प्रकार बढ़ाया कि DE = AD,BE को मिलाया ।
उपपत्ति :ΔADC तथा ΔEDB में ,
DC = DB (दिया है )
AD = ED (निर्माण द्वारा )
∠ADC=∠EDB (शीर्षाभिमुख कोण )
∴ΔADC≅ΔEDB (SAS द्वारा )
⇒AC=EB तथा ∠DAC=∠DEB (CPCT)
किन्तु ∠DAC=∠BAD (.∵AD,∠A को समद्विभाजित करता है ।)
∴AB=BE
⇒BE=AC
अतः AB = AC
Topper's Solved these Questions
- त्रिभुजों की सर्वांगसमता Book:BALAJI PUBLICATIONChapter:त्रिभुजों की सर्वांगसमता Exercise:अभ्यास प्रश्न 12.1
Explore 11 Videos
- त्रिभुजों की सर्वांगसमता Book:BALAJI PUBLICATIONChapter:त्रिभुजों की सर्वांगसमता Exercise:अभ्यास प्रश्न 12.2
Explore 4 Videos
- त्रिभुज एवं उसके गुण Book:BALAJI PUBLICATIONChapter:त्रिभुज एवं उसके गुण Exercise:स्वमूल्यांकन परिक्षण ( Self Assessment Test)
Explore 13 Videos
- दो चरो के रैखिक समीकरण Book:BALAJI PUBLICATIONChapter:दो चरो के रैखिक समीकरण Exercise:स्वमूल्यांकन परीक्षण
Explore 18 Videos
Similar Questions
चित्र में वर्ग ABCD में एक बिंदु X है । AX पर एक वर्ग AXYZ बनाया जाता है ।
सिद्ध कीजिए किBX = DZ

View Solutionदिये गये चित्र में यदि ∠X=∠Y तथाAB=CB तब सिद्ध कीजिए कि AE = CD
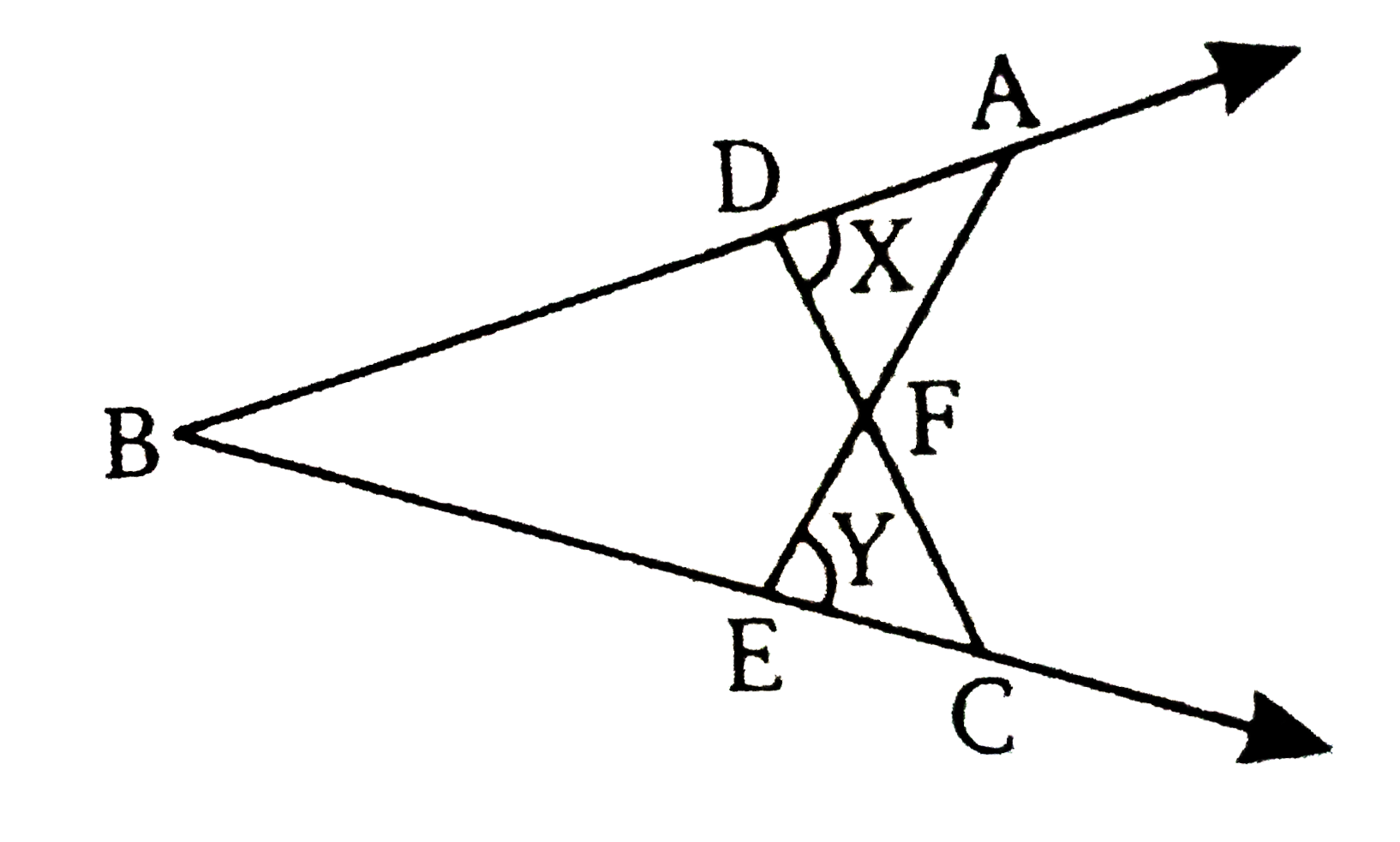
View Solutionयदि एक त्रिभुज का एक कोण, अन्य दो के योग के बराबर है तब सिद्ध कीजिए की त्रिभुज एक समकोण त्रिभुज है।
View Solutionएक पुस्तक का मूल्य, एक पैन के मूल्य से दो गुना है | इसे व्यक्त करने के लिए दो चरो का रैखिक समीकरण लिखिये |
View Solutionएक समकोण समद्विबाहु त्रिभुज के कर्ण का समीकरण 3x+4y=4 है । यदि इसके सम्मुख शीर्ष के निर्देशांक (2,2)है , तो त्रिभुज की शेष दो भुजाओ के समीकरण ज्ञात कीजिए ।
View Solutionकिसी समबाहु त्रिभुज के आधार का समीकरण x+y=2 है तथा सामने के शीर्ष के निर्देशांक (2,1) है , त्रिभुज की शेष भुजाओ के समीकरण ज्ञात कीजिए ।
View Solutionमाना A(2,−3) तथा B(−2,1) एक त्रिभुज ABC के शीर्ष है । यदि इस त्रिभुज का केन्द्रक सरल रेखा 2x+3y=1पर भ्रमण करता है तो शीर्ष C का बिन्दुपथ है -
View Solutionसिद्ध कीजिए कि ΔABC एक समद्विबाहु त्रिभुज है यदि
∣∣ ∣ ∣∣1111+cosA1+cosB1+cosCcos2A+cosAcos2B+cosBcos2C+cosC∣∣ ∣ ∣∣=0
View Solutionवह त्रिभुज जिसका लांबकेंद्र त्रिभुज का शीर्ष बिंदु होता है ,कहलाता है -
View Solutionएक ही आधार BC पर तीन समद्विबाहु त्रिभुज △PBC ,△QBC और △RBC स्तिथ है। सिद्ध कीजिए कि P ,Q और R समरेख है।
View Solutionयदि सदिश 10¯i−5¯j+10¯k किस त्रिभुज के आधार को निरूपित करता है तथा इस आधार की सम्मुख शीर्ष से दूरी 8 मात्रक हो तो त्रिभुज का क्षेत्रफल ज्ञात कीजिए।
View Solutionसदिश विधि से सिद्ध करें कि यदि किसी त्रिभुज दो मध्यिकाएँ बराबर हों, तो त्रिभुज समद्विबाहु होता है |
View Solutionएक समकोण समद्विबाहु त्रिभुज के कर्ण का समीकरण 3x+4y=4 है। यदि इसके सम्मुख शीर्ष के निर्देशांक (2,2) हो तो त्रिभुज की शेष दो भुजाओं के समीकरण ज्ञात कीजिए।
View Solutionमान A(2,−3) तथा B(−2,1) एक त्रिभुज ABC के शीर्ष है। यदि इस त्रिभुज का केन्द्रक सरल रेखा 2x+3y=1 पर भ्रमण करता है, तो शीर्ष C का बिन्दुपथ है:
View Solutionएक त्रिभुज का एक शीर्ष (1,2) पर है तथा इससे होकर जाने वाली दो भुजाओं के मध्य - बिन्दु (−1,1) और (2,3) हैं , तो इस त्रिभुज का केन्द्रक है
View Solutionयदि एक त्रिभुज , जिसका एक शीर्ष परवलय के शीर्ष परवलय y2+4(x−a2)=0 तथा अन्य दोनों शीर्ष y-अक्ष तथा परवलय के प्रतिच्छेदन बिंदुओं पर हैं , का क्षेत्रफल 250 वर्ग इकाई है , तो 'a' का एक मान है
View Solution

