The work done by the tension in the strings of a simple pendulum in one complete oscillation is equal to

Video Solution

Text Solution

Verified by Experts

Consider a conical pendulum of string length L with its bob of mass m performing UCM along a path of radius r. Let v be the cosntant linear speed of the bob and $\to F$ the tension in the string.
Resolve $\to F$ into components $F cos θ$ vertically opposite to the weight of the bob and $F sin θ$ horizontal, $F cos θ$ balances the weight . $F sin θ$ is teh necessary centripetal force.
$∴ F sin θ = \frac{m v^{2}}{r}' ... (1)$
and $F cos θ = m g . . (2)$
Dividing Eq. (1) by Eq. (2),
$tan θ = \frac{v^{2}}{r g} ... (3)$
Also, from the diagram,
$tan θ = \frac{P C}{O C} \frac{r}{h} ... (4)$
where OC = h = L cos $θ$ is the axial height of the cone. Therefore, from Eqs. (3) and (4),
$\frac{v^{2}}{r g} = \frac{r}{h} ∴ \frac{v^{2}}{r} = \frac{r g}{h} ... (5)$

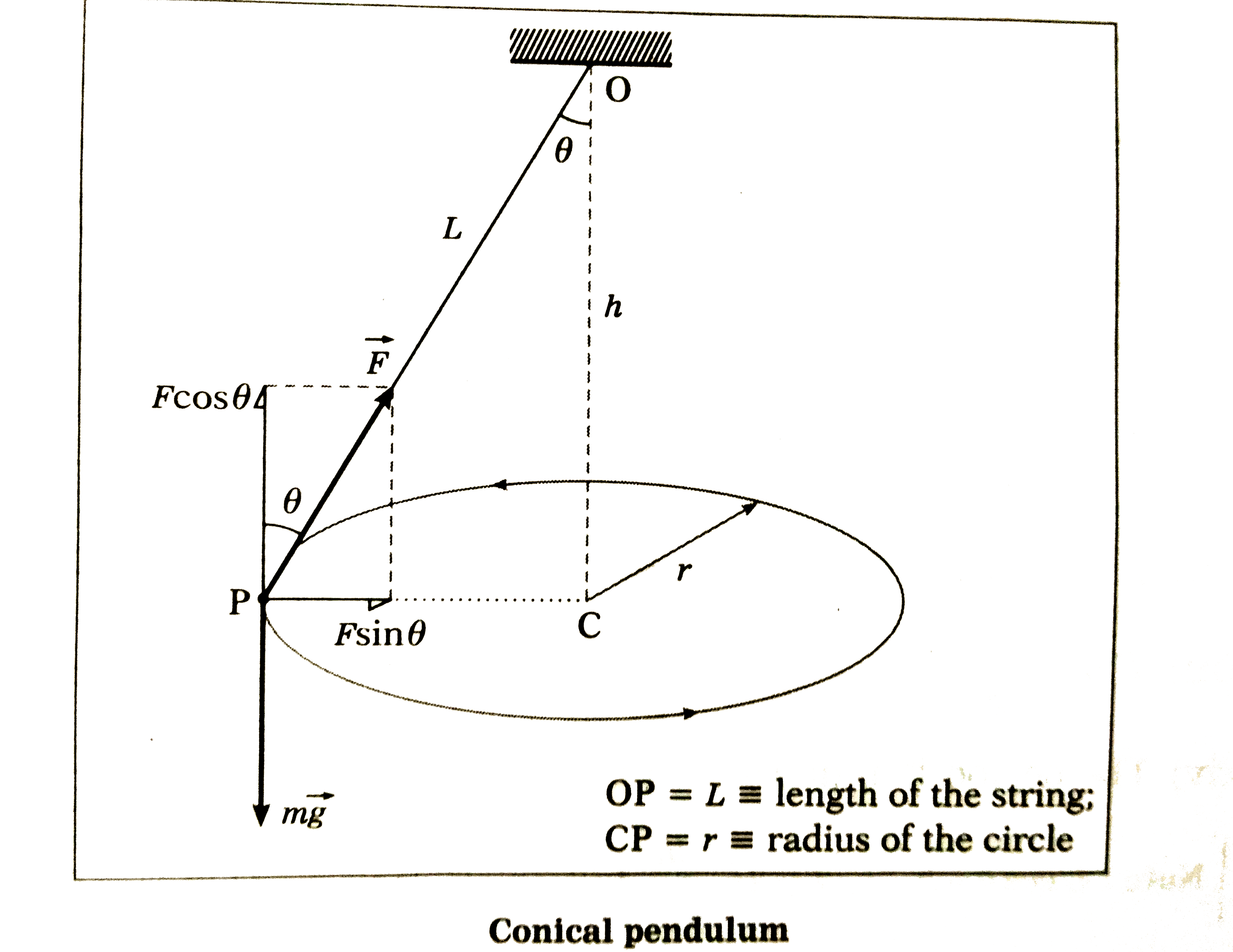
Squaring and adding Eqs. (1) and (2)
$F^{2} {sin}^{2} θ + F^{2} {cos}^{2} θ = {(\frac{m v^{2}}{r})}^{2} + {(m g)}^{2}$
$∴ F^{2} = {(\frac{m r g}{h})}^{2} + {(m g)}^{2} = {(m g)}^{2} [{(\frac{r}{h})}^{2} + 1]$
$∴ F = m g \sqrt{{(\frac{r}{h})}^{2} + 1} = m g \sqrt{{(\frac{r}{L cos θ})}^{2} + 1}$
This is the expression for the tension in the string.

Updated on:21/07/2023