A pilot in an aeroplane observes that Vashi bridge is one side of the plane and Worli sea - link is just on the oposite side . The angles of depressons of Vashi bridge and Wrli sea - link are 60∘and30∘ respectively . If the aeroplane is at a height of 5500√3m at that time , what is the distance between Vashi bridge and Wrli sea - link ?
The correct Answer is:The distance between the Vashi bridge and Worli sea-link is 22 km.
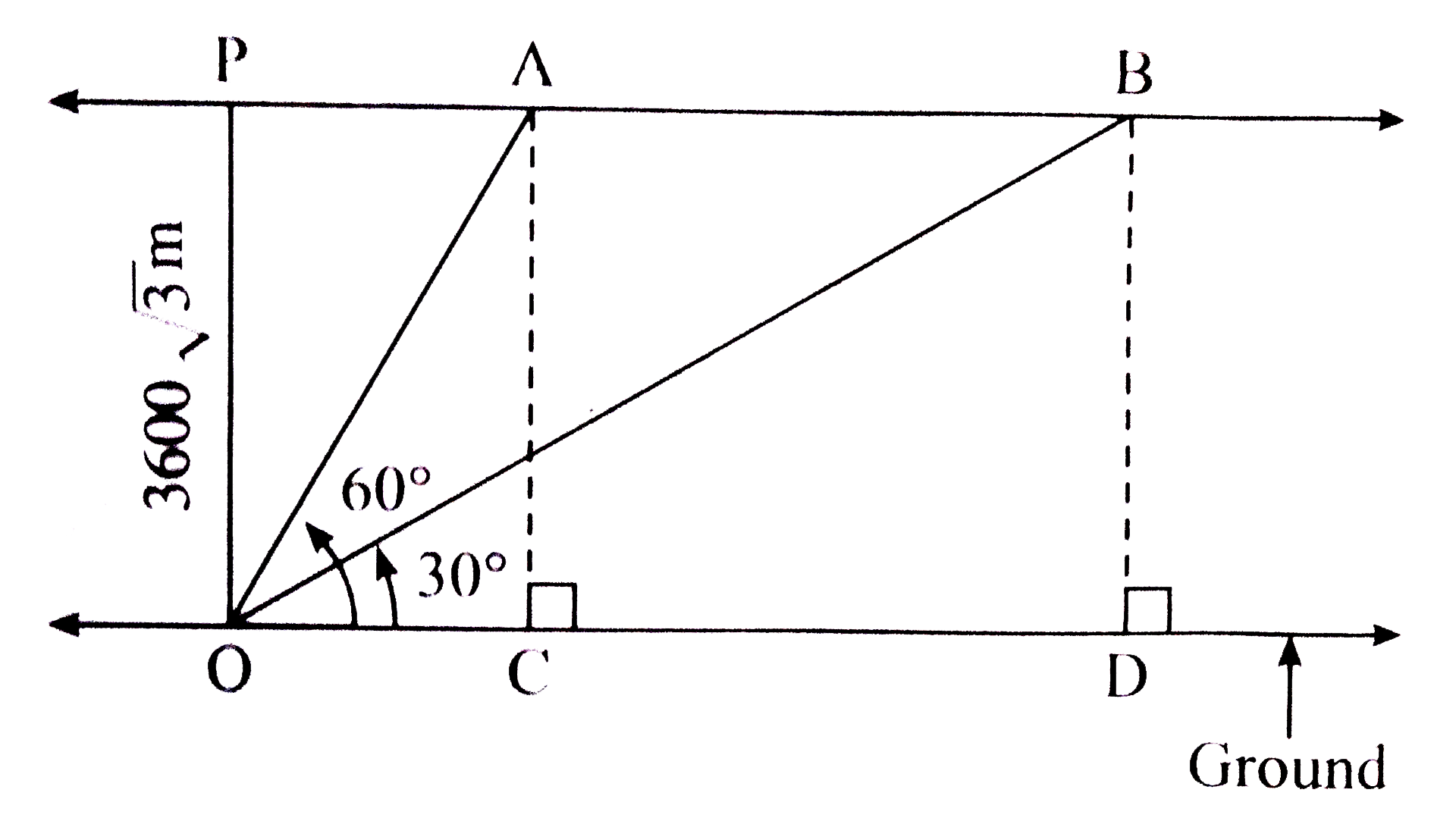
Let P be the position of the plane . Q is a point on the ground such that the perpendicular distance QP=5500√3m
V is the position of Vashi bridge and W the position of Worli sea- link
From the figure , ∠PWQ=∠BPW=30∘ ...(Alternate angles )
Now, in right angled ΔPVQ,
tan∠PVQ=tan60∘=PQVQ∴√3=5500√3VQ
∴VQ=5500√3VQ∴VQ=5500m ... (1)
∴VQ=5500√3VQ ∴VQ=5500m ... (1)
In right angled ΔPWQ ,
tan∠PWQ=tan30∘=PQWQ
∴1√3=5500√3WQ
∴WQ=5500√3×√3∴WQ=5500×3
∴WQ=16500m ...(2)
VW=VQ+QW ...(V−Q−W)
=(5500+16500)m ... [ From (1) and (2) ]
∴VW=22000m=22km
Topper's Solved these Questions
- CHALLENGING QUESTIONSBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CHALLENGING QUESTIONSEXERCISE - SECTION 3 (MODEL QUESTION PAPER FOR PRACTICE )
7 Videos
- CHALLENGING QUESTIONSBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CHALLENGING QUESTIONSEXERCISE - SECTION 3 (MODEL QUESTION PAPER FOR PRACTICE ) Choose the correct alternative :
3 Videos
- CHALLENGING QUESTIONS BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CHALLENGING QUESTIONS EXERCISE - EXAMPLE FOR PRACTICE
22 Videos
- CIRCLEBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CIRCLEEXERCISE - Challenging Questions
10 Videos
Similar Questions
From a point an a bridge across river, the angles of depression of the banks on opposite sides of the river are 30∘and45∘ respectively. If the bridge is at a height of 3 m from the banks, find the width of the river.
View SolutionThe angles of elevation of an aeroplane from two places 10 km apart are found to be 60∘and30∘ respectively. Find the height of the aeroplane.
View Solution
Knowledge Check
Two men are on the opposite sides of a tower. They measure the angles of elevation of the top of the tower as 45∘ and 30∘ respectively. If the height of the tower is 40 m, then the distance between the men is
A40 mB40√3mC68.28 mD109.28 mTwo ships are sailing in the sea on the tow sides of a light house . The angles of elevation of the top of the light house as observed from the two ships are 30∘and45∘ respectively . If the light house is 100 m high , the distance be - tween the two ships is :(take √3=1.73)
Aa)173 metreBb)200 metreCc)273 metreDd)300 metreFrom two points A and B on the same side of a building the angles of elevation of the top of the building are 30∘and60∘ respectively. if the height of the building is 10 m find the distances between A and B correct to two decimal places
A10 . 66 mB13 . 43 mC11 . 55 mD12 . 26 m
From a point on a bridge across a river, the angles of depression of the banks on opposite sides, of the river are 30° and 45° respectively. If the bridge is at a height of 3 m from the banks, find the width of the river.
View SolutionFrom a point A on a bridge across a river, the angles of deression of the banks on opposite side of the river are 30∘and45∘, respectively. If the bridge is at a height of 9 m from the suface of river, then find the width of the river.
View SolutionFrom a point of a bridge across a riuver, the angles of depression of the banks on opposite sides of the river are 30∘ and 45∘, respectively. IF the bridge is at a height of 10 m from the banks, then find the width of the river. (Use √3=1.73)
View SolutionFrom a point on a bridge across a river the angles of depression of the banks on opposite side of the river are 30o and 45o respectively. If bridge is at the height of 30m from the banks, find the width of the river.
View SolutionAn aeroplane at an altitude of 1200 metres finds that two ships are sailing towards it in the same direction. The angles of depression of the ships as observed from the aeroplane are 60o and 30o respectively. Find the distance between the two ships.
View Solution
