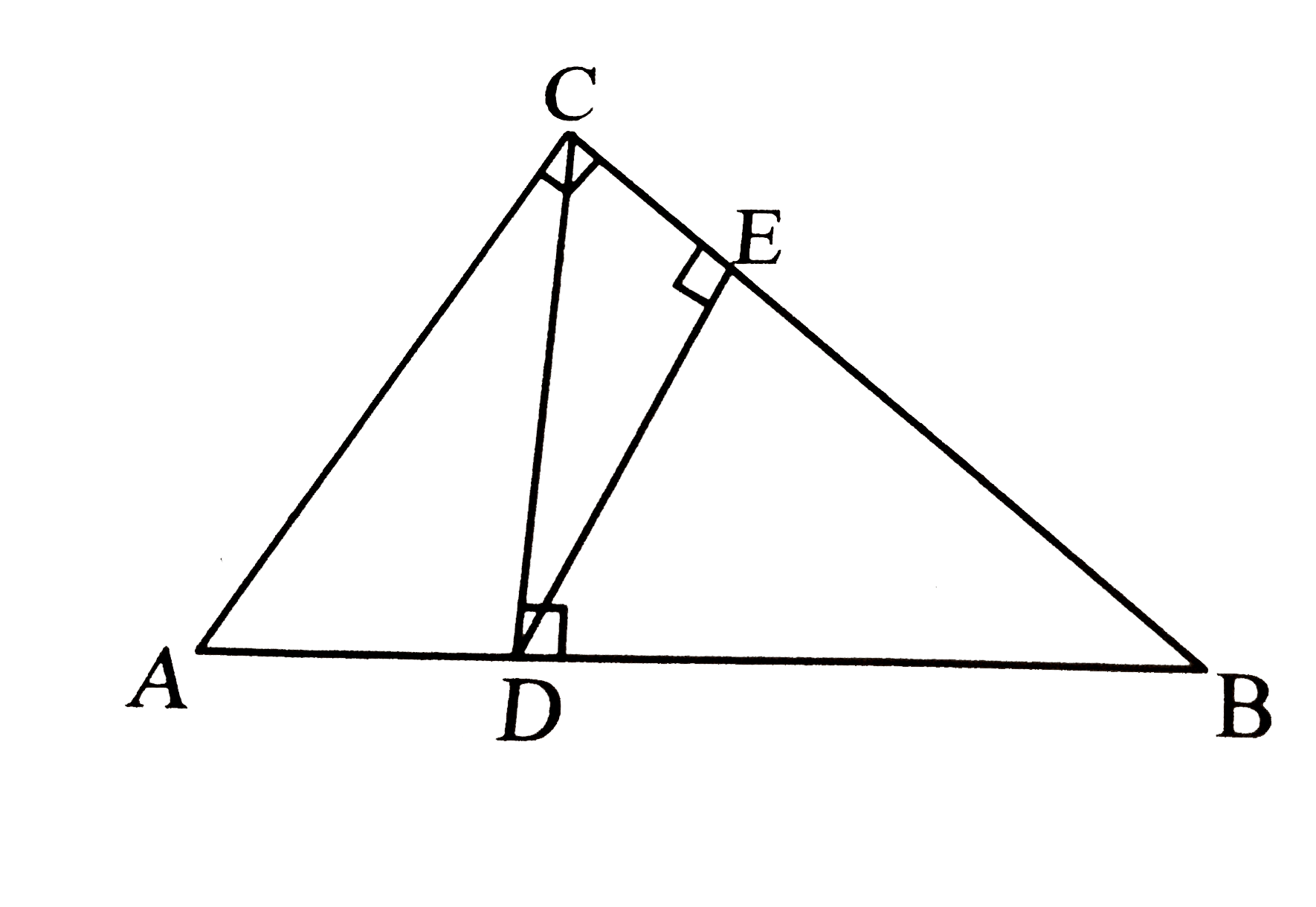
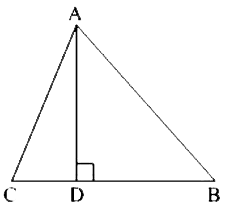
In ΔABC,∠ACB=90∘
seg CD ⊥ seg AB
seg DE ⊥ seg CB.
Show that: CD2×AC=AD×AB×DE
Video Solution
Text Solution
In ΔACB,∠ACB=90∘
seg CD⊥ hypotenuse AB …(Given)
∴ by therorem of geometric mean
CD2=AD×DB …(i)
In ΔACBandΔDEB,
In ΔACBandΔDEB,
∠ACB≅∠DEB ...(Each measures (90∘)
∴ΔACB~ΔDEB ...(A A test of similarity )
ACDE=ABDB ...( Corresponding sides of similar Deltas )
∴AC=ABDB×DE
Multiplying (1) and (2)
CD2×AC=AD×DB×ABDB×DE
∴CD2×AC=AD×AB×DE
|
Topper's Solved these Questions
- CHALLENGING QUESTIONSBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CHALLENGING QUESTIONSEXERCISE - SECTION 3 (MODEL QUESTION PAPER FOR PRACTICE )
7 Videos
- CHALLENGING QUESTIONSBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CHALLENGING QUESTIONSEXERCISE - SECTION 3 (MODEL QUESTION PAPER FOR PRACTICE ) Choose the correct alternative :
3 Videos
- CHALLENGING QUESTIONS BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CHALLENGING QUESTIONS EXERCISE - EXAMPLE FOR PRACTICE
22 Videos
- CIRCLEBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CIRCLEEXERCISE - Challenging Questions
10 Videos
Similar Questions
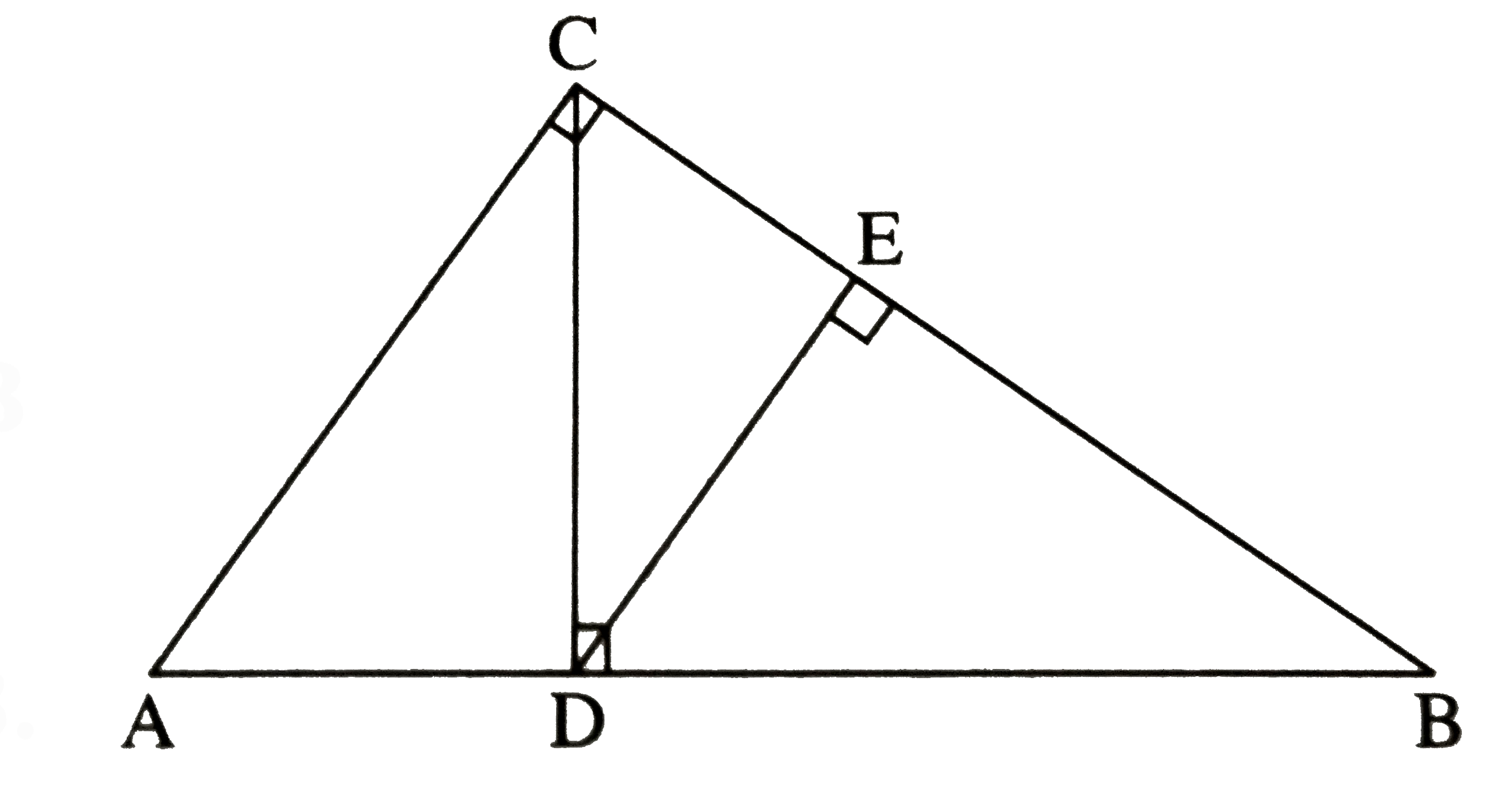
In △ ABC ,
∠ACB=90∘ ,
CD⊥AB and
DE⊥CB
Prove that CD2×AC=AD×AB×DE .
View SolutionIn ΔABC,∠A=90∘, seg BP⊥ side AC.AP=2,PC=8. Find BP.
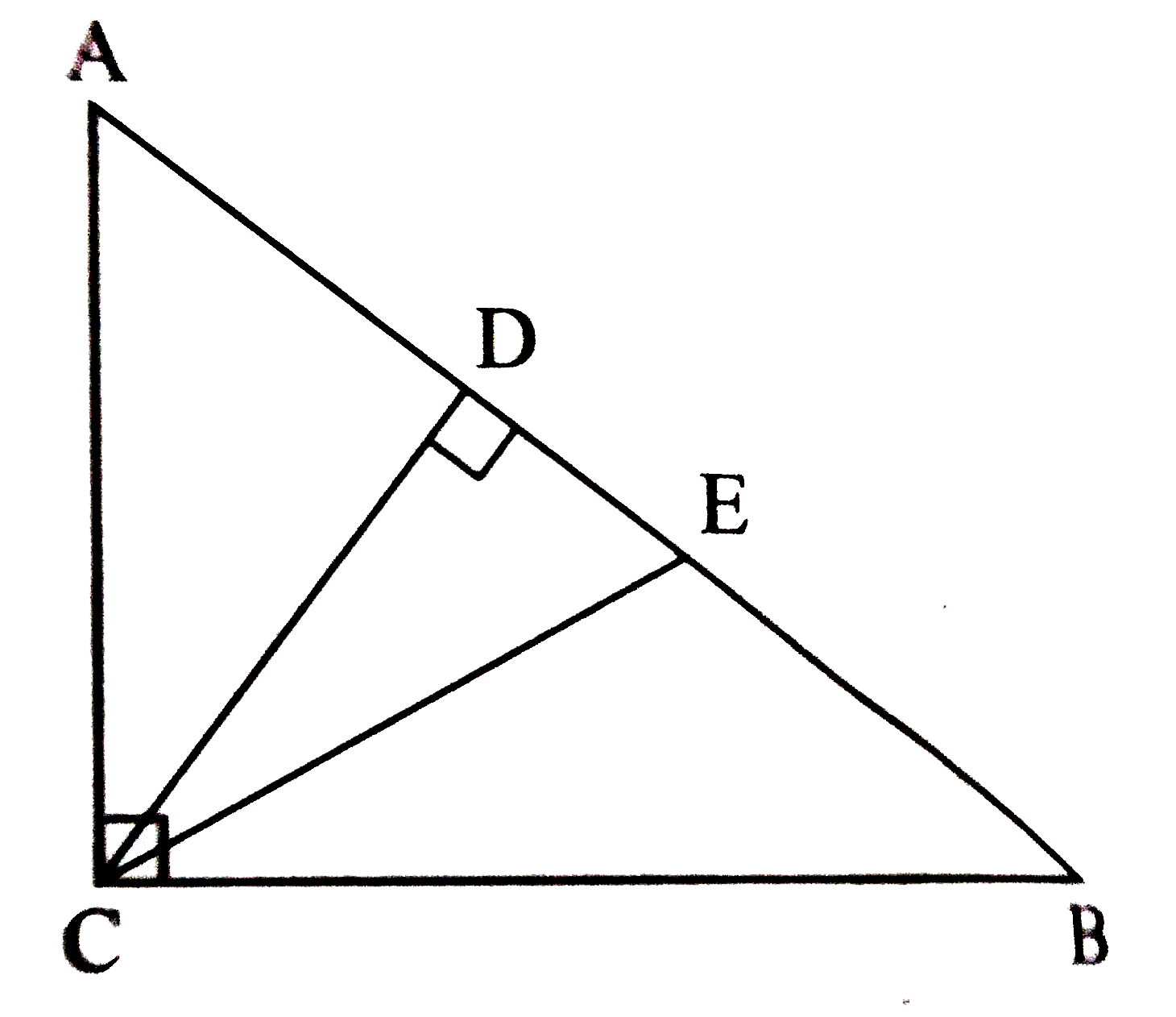
View SolutionIn ΔABC,∠ACB=90∘, seg CD⊥ side AB and seg CE is angle bisector of ∠ACB
Prove : ADBD=AE2BE2
View SolutionIn ΔPQR,∠PQR=90∘,segQS⊥segPR, then find x,y,z.
View SolutionIn ΔPQR,∠PQR=90∘,
seg QS⊥ seg PR then find x,y,z.
View SolutionIn ΔPQR,∠Q=90∘, seg RS⊥ side PR. If PQ=16,QR=30. Find QS.
View SolutionIn ΔABC,∠BAC=90∘, seg BL and seg CM are median of ΔABC. Then prove that: 4(Bl2+Cm2)=5BC2
View SolutionIn ΔPQR,∠PQR=90∘andsegQS⊥ hypotnuse PR,-P-S-R,then
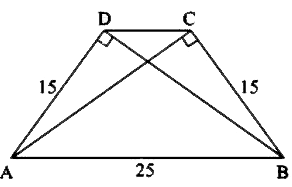
View SolutionIn a trapezium ABCD seg AB∣∣segDC
seg BD⊥segAD,
seg AC⊥segBC,
If AB=25. Find A(□ABCD)
View SolutionIn ΔABC, seg AD⊥ seg BCDB=3CD.
Prove that : 2AB2=2AC2+BC2
View Solution
