Tangent Secant Theorem
Point E is in the exterior of a circle. A secant through E intersects the circle at points A and B, and a tangent through E touches the circle at point T, then EA×EB=ET2.
Given : (1) A circle with centre O
(2) Tangent ET touches the circle at pointT
(3) Secant EAB intersects the circle at points A and B .
To prove : EA×EB=ET2
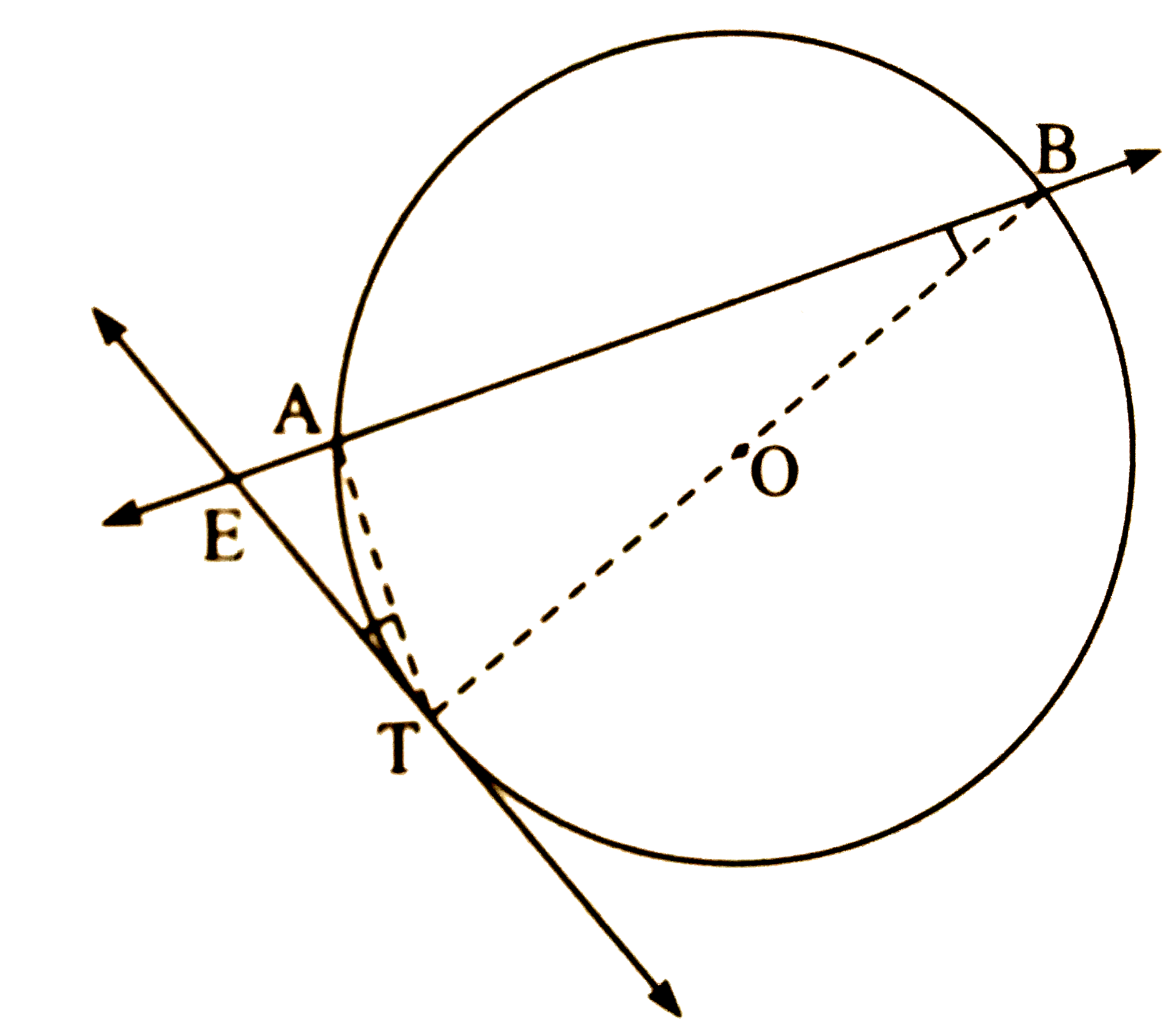
Proof : In ΔETA and ΔEBT,
∠AET≅∠TEB …..(Common angle )
∠ETA≅∠EBT …(Tangent secant theorem )
∴ΔETA~ΔEBT …...(AA test of similarity )
∴ETEB=EAET ......(Corresponding sides of similar triangles are in proportion )
∴EA×EB=ET×ET
∴EA×EB=ET2
Topper's Solved these Questions
- THEOREMS BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - THEOREMS EXERCISE - PYTHAGORAS THEOREM
4 Videos
- STATISTICSBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - STATISTICSEXERCISE - EXAMPLES FOR PRACTICE (MCQs)
35 Videos
- TRIGONOMETRYBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - TRIGONOMETRYEXERCISE - CHALLENGING QUESTIONS
6 Videos
Similar Questions
Knowledge Check
O is the centre of a circle of radius 5cm. T is a point such that OT=13cmandOT intersects the circle at E. If AB is the tangent to the circle at E, find length of AB.
A20 cmB203cmC10cmD25 cmType V: O is the center of the circle of radius 5cm. T is a point such that OT=13cm and OT intersects the circle at E . If AB is the tangent to the circle at E; find the length of AB.
A103B203C163DCannot be determined
In the figure, a tangent segment PA touches the circle at point A and secant PBC intersects the circle at points B and C. If AP=15 cm and BP=10, then find BC.
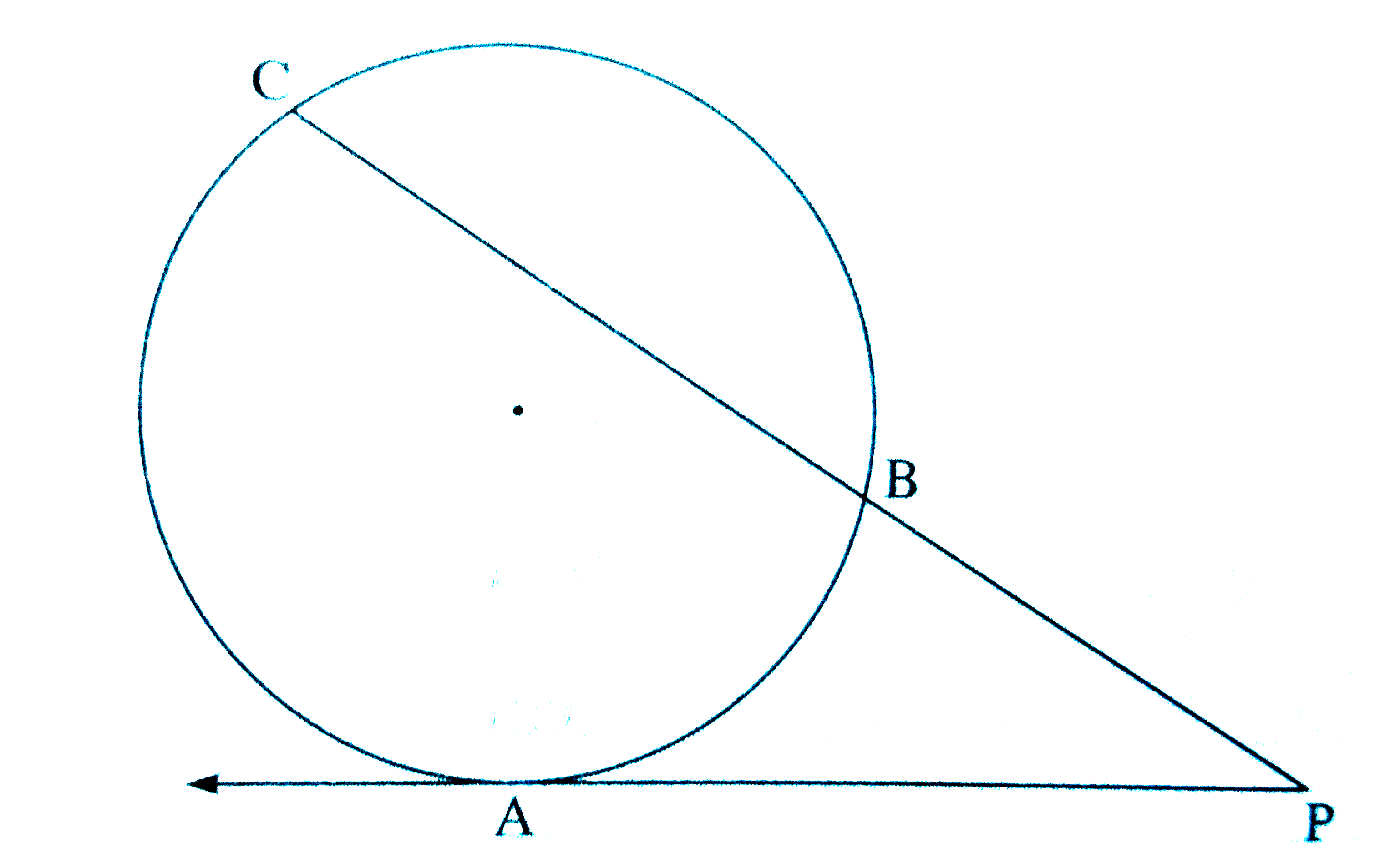
View SolutionLet PAB be a secant to a circle intersecting at points A and B, and PC is a tangent. Which one of the following is correct?
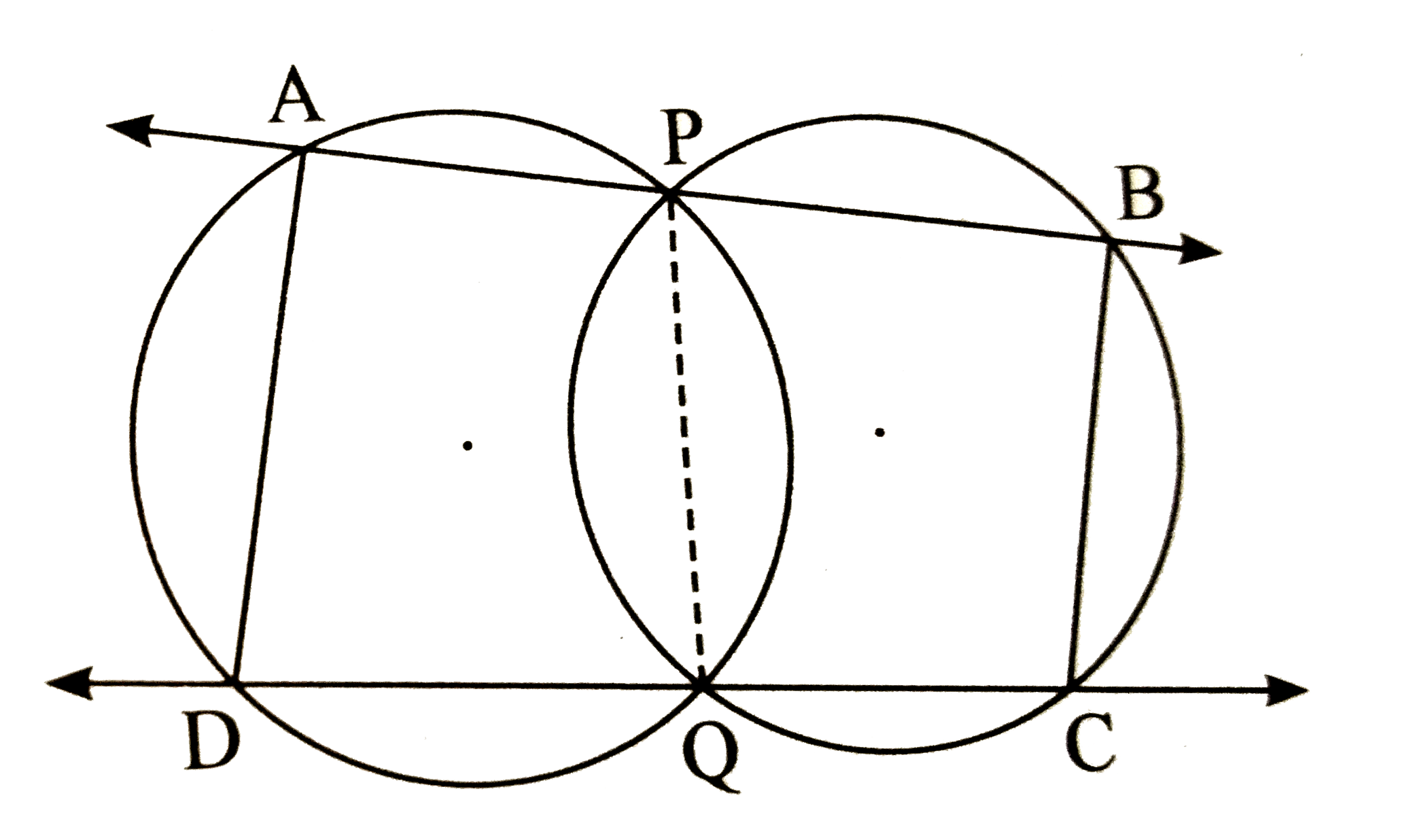
View SolutionTwo circles intersect each other at point P and Q. Secants drawn through p and Q intersect the circles at points A,B and D,C
Prove that :∠ADC+∠BCD=180∘
View SolutionIn the figure, two circles intersect each other in points P and Q. If tangent from point R touch the circles at S and T, then prove that RS=RT.

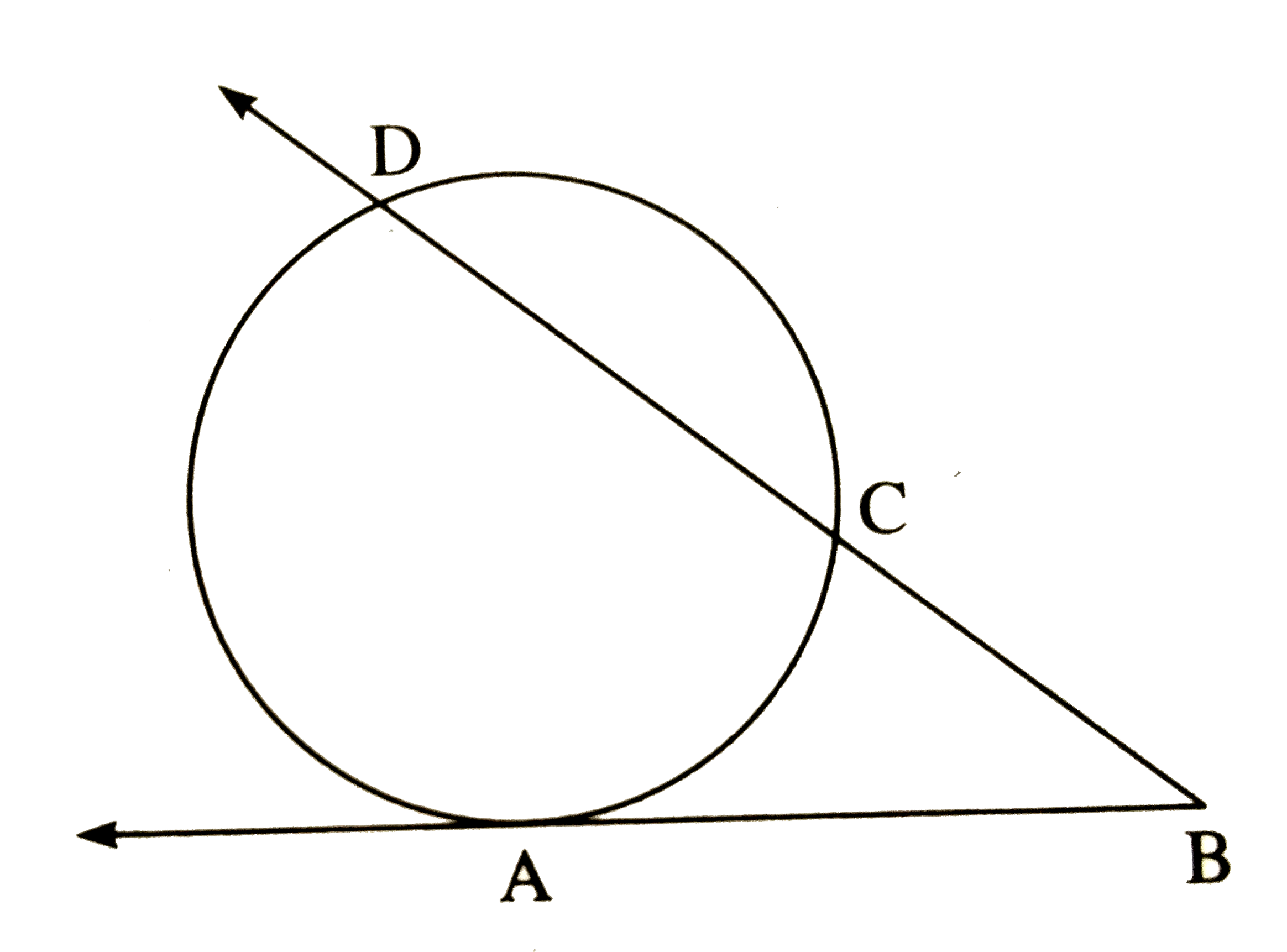
View SolutionRay BA is tangent at point A . Ray BD is secant intersecting the circle at points C and D then
BA2=□×□
View SolutionO is the centre of a circle of radius 5cm. T is a point such that OT=13cm and OT intersects the circle at E. If AB is the tangent to the circle at E, find length of AB.
View Solution

