Construct a word problem on quadratic equation, such that one of its answers is 20 ( years, rupee, centimetre , etc. ) Also solve it.

Video Solution

Text Solution

Verified by Experts

The correct Answer is:Sneha's present age is 20 years.

Word problem on quadratic question $:$
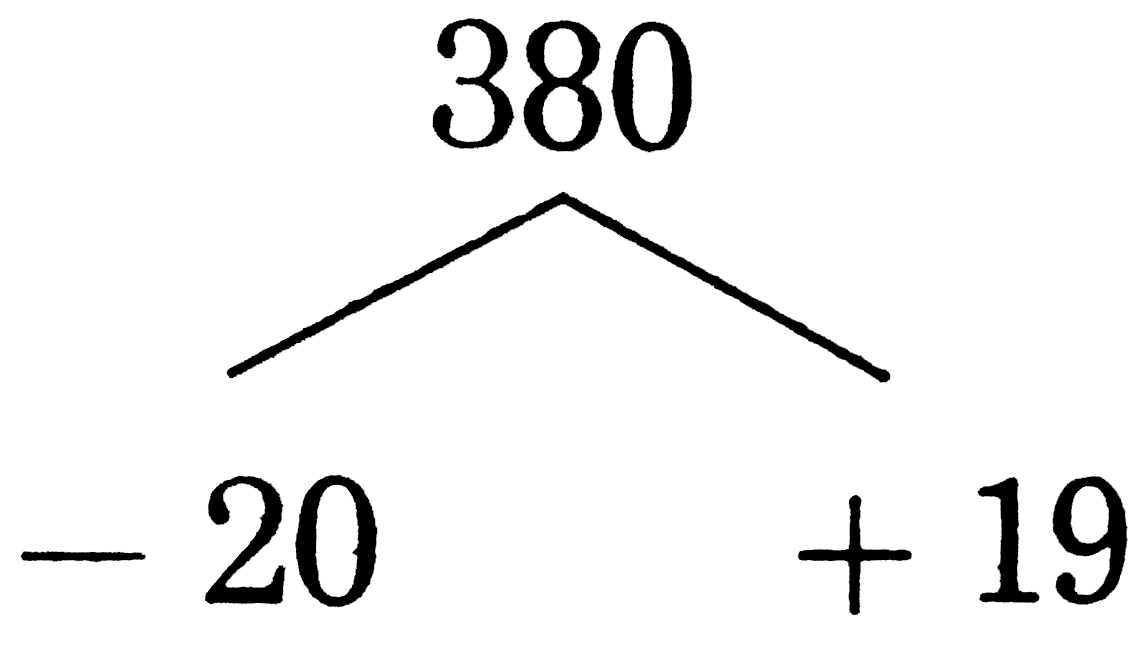
The product of Sneha's age 5 years ago and 14 years hence is numerically 360. Find the present age.
Solution $:$ Let Sneha's presentage by x years.
Her age 5 years ago was ( x-5) years.
Her age 4 years hence willbe ( x+4) years.
The numbers denoting her ages are ( x-5) and ( x+4)
From the given condition.
$(x - 5) (x + 4) = 360$
$∴ x (x + 4) - 5 (x + 4) = 360$
$∴ x^{2} - x - 20 - 360 = 0$
$∴ x^{2} - x - 380 = 0$
$∴ x (x - 20) + 19 (x - 20) = 0$
$∴ (x - 20) (x + 19) = 0$
$x - 20 = 0$ or $x + 19 = 0$
$∴ x = 20$ or $x = - 19$
But the age cannot be negative
$∴ x = - 19$ is unacceptable.
$∴ x = 20$

|

Updated on:21/07/2023

Class 10 MATHS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
If the quadratic equation $a x^{2} + b x + c = 0$ has $- 2$ as one of its roots then $a x + b y + c = 0$ represents
AA family of concurrent lines
BA family of parallel lines
CA single line
DA line perpendicular to x - axis
Question 2 - Select One
Two students solved a problem involving a quadratic equation. The first student made an error only in the constant term of the equation and determined the roots were 2 and 8. The second student made an error only in the coefficient of the linear term and determined the roots were -1 and -9. What was the quadratic equation ?
A $x^{2} - 10 x + 9 = 0$
B $x^{2} - 10 x + 9 = 0$
C $x^{2} - 10 x + 16 = 0$
D $x^{2} - 8 x - 9 = 0$
Question 3 - Select One
Ankur got zero marks in a word problem on linear equations in an assessment. The teacher knows that he can solve linear equations correctly. The teacher ought to remark in his report
AAnkur has a problem in comprehending the language of the question, though he can solve the equations
BAnkur lacks concentration and hence has examination phobia
CAnkur is not studying and practising at home
DAnkur has not understood the concept of linear equations completely

NAVNEET PUBLICATION - MAHARASHTRA BOARD-MODEL QUESTION PAPER-SOLVE THE FOLLOWING SUBQUESTIONS: (ANY ONE)

Home
Ask Doubt
Profile