A game of chance consist of spinning an arrow which comes to rest pointing at one of the numbers 15,20,25,30,35,40,45,50 and these are equally likely outcomes. What is the probability that it will point at
(i) an even number? (ii) at a number multiple of 5
(iii) at a number divisible by 3 (iv) at a prime number.
The sample is
S={15,20,25,30,35,40,45,50}:n(S)=8
(i) Let A be the event that arrow points at an even number.

Then A={20,30,40,50}∴n(A)=4
∴P(A)=n(A)n(S)P(A)=48=12
(ii) Let B be the event that the arrow points at a number multiple of 5.
Then B={15,20,25,30,35,40,45,50}∴n(B)=8
P(B)=n(B)n(S)∴P(B)=88=1
(iii) Let C be the event that the arrow points at a number divisible by 3.
Then C={15,30,45}∴n(C)=3
P(C)=n(C)n(S)∴P(C)=38
(iv) Let D be the even the arrow points at a prime number.
Then D={},∴n(D)=0
∴P(D)=n(D)n(S)∴P(D)=08=0
Ans (i) 12 (ii) 1 (iii) 38 (iv) 0
Topper's Solved these Questions
- CHALLENGING QUESTIONS Book:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:CHALLENGING QUESTIONS Exercise:EXAMPLE FOR PRACTICE
Explore 22 Videos
- BOARD'S QUESTION PAPER : MARCH 2019Book:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:BOARD'S QUESTION PAPER : MARCH 2019Exercise:QUESTION
Explore 30 Videos
- CHALLENGING QUESTIONSBook:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:CHALLENGING QUESTIONSExercise:SECTION 3 (MODEL QUESTION PAPER FOR PRACTICE ) Solve any one of the following subquestions :
Explore 1 Video
Similar Questions
A game of chance consists of spinning an arrow which comes to rest pointing at one of the numbers 1,2 3,4,5,6,7,8 and these are equally likely outcomes what is the probability that it will point at :
(i) 8?
(ii) an odd number ?
(iii) a number greater than 2 ?
(iv) a number less than 9 ?
View SolutionA game of chance consists of spinning an arrow which comes to rest pointing at one of the numbers 1, 2, 3, 4, 5, 6, 7, 8 (See Fig. 131), and these are equally likely outcomes. What is the probability that it will point at (i) 8? (ii) an odd number? (iii) a number greater than 2? (iv) a number less than 9?
View Solution
Knowledge Check
A game of chance consists of spinning an arrow, which comes to rest pointing at one of the numbers 1,2,3,4,5,6,7,8 and these are equally likely outcomes. Find the probability that the arrow will point at any factor of 8.
A58B78C18D38
A game of chance consists of spinning an arrow which comes to rest pointing at one of the numbers 1,2,3,4,5,6,1,8 (see Figure), and these are equally likely outcomes. What is the probability that it will point at(i) 8?(ii) an odd number?(iii) a number greater than 2?(iv) a number less than 9?
View SolutionA game of chance consists of spinning an arrow which comes to rest pointing at one of the numbers 1, 2, 3, 4, 5, 6, 7, 8 (see figure) and these are equally likely outcomes. What is the probability that it will point at :
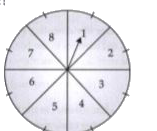
(i) 8? (ii) an odd number?
(iii) a number greater than 2? (iv) a number less 9?
View SolutionIn a game of chance, a spining arrow comes to rest at one of the numbers
1,2,3,4,5,6,7,8,
All these are equally likely outcomes.
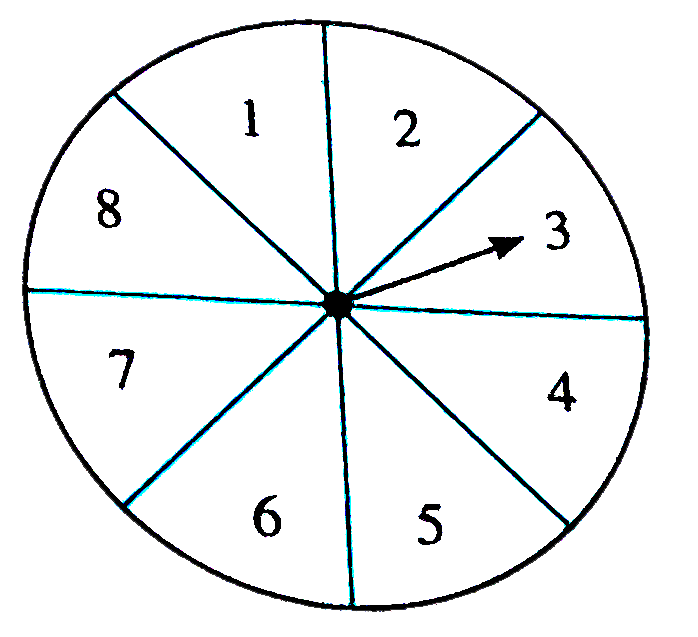
Find the probability that it will rest at
View SolutionA game of chance consists of spinning an arrow which is equally likely to come to rest pointing to one of the numbers 1, 2, 3……., 12 as shown in the Fig. What is the probability that it will point to:
(i) 6? (ii) an even number? (iii) a prime number? (iv) a multiple of 4?

View SolutionRead the following text and answer the following question on the basis of the same.
A game of chances consisting of spinning an arrow which comes to rest pointing at one of the numbers 1, 2, 3, 4, 5, 6, 7, 8 (see the figure) and these are equally likely outcomes.
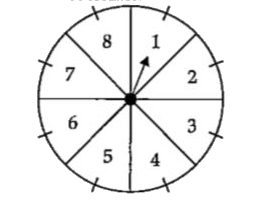
What is the probability that it will point at a number greater than 2?
View Solutiona game of chance consists of spinning an arrow which is equally likely to come to rest pointing to one of the numbers 1,2,3,….,12 as shown in the figure. What is the probability that it will point to
(i) 6? (ii) an even numbers?
(iii) a prime number? (iv) a number which is a multiple of 5?

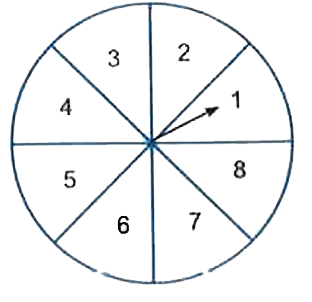
View SolutionA game of chance consists of spinning an arrow on a circular board, divided into 8 equal parts, which comes to rest pointing at one of the numbers 1,2, 3, ..., 8 , which are equally likely outcomes. What is the probability that the arrow will point at (i) an odd numbei ? (ii) a number greater than 3? (Hi) a number less than 9?
View Solution

