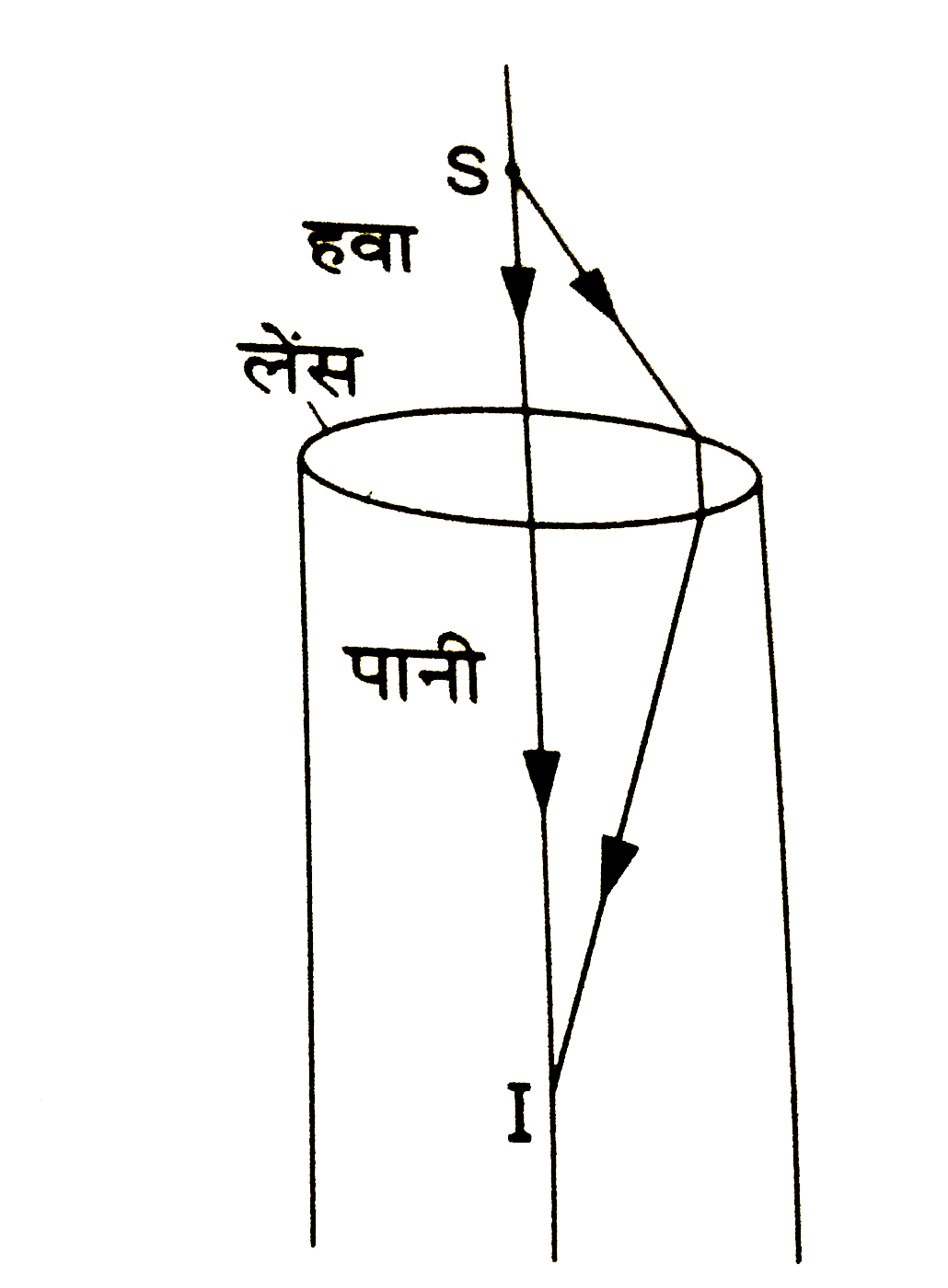
पानी से भरे एक बेलनाकार बरतन को ऊपर से एक उत्तल लेंस व्दारा ढँक दिया गया हैं । हवा में लेंस की फोकस - दूरी 10 cm हैं और इसकी दोनों सतहों की वक्रता - त्रिज्याएँ बराबर हैं । एक बिदुस्त्रोत को अक्ष पर लेंस से 21 cm दूर हवा में रखा गया हैं । काँच का अपवर्तनांक 3/2 तथा पानी का अपवर्तनांक 4/3 लेते हुए स्त्रोत के अंतिम प्रतिबिंब का स्थान ज्ञात करें ।
लेंस की दोनों सतहें उत्तल हैं । यदि इनकी वक्रता - त्रिज्याएँ R0 हो , तो पहली सतह के लिए R1=+R0 तथा दूसरी सतह के लिए , R2=−R0.
अतः , सूत्र 1f=(n−1)(1R1−1R2) से ,
110cm=(32−1)(1R0+1R0)
या R0=10cm .
प्रश्न में दी गई परिस्थिति चित्र में दिखाई गई हैं । पहली सतह पर अपवर्तन के लिए ,
u=−21cm,R=10cm,n1=1,n2=32.
सूत्र n2v−n1u=n2−n1R से ,
32v1−1−21cm=32−110cm
v1=630cm.
अतः , पहले प्रतिबिंब की दूरी , v1=630 cm .
अर्थात् , इस अपवर्तन के बाद चलती किरणें जो दूसरी सतह पर आपतित हो रही हैं , सतह से 630 cm आगे कटेगी । चूँकि लेंस पतला हैं इसलिए दूसरी सतह से भी इस बिंदु की दूरी इतनी ही ली जाएगी । इस अपवर्तन के लिए ,
u=+630cm,R=−10cm,n1=32,n2=43.
अतः ,43v−32×630cm=43−32−10cm
या v = 70 cm .
अर्थात अंतिम प्रतिबिंब पानी में लेंस से 70 cm दूरी पर बनेगा ।
Topper's Solved these Questions
- गोलीय सतहों पर अपवर्तन BOOK - HC VERMA HINDICHAPTER - गोलीय सतहों पर अपवर्तन EXERCISE - अभ्यास
5 Videos
- गोलीय सतहों पर अपवर्तन BOOK - HC VERMA HINDICHAPTER - गोलीय सतहों पर अपवर्तन EXERCISE - विचार हेतु प्रश्न
6 Videos
- गुरुत्वाकर्षण BOOK - HC VERMA HINDICHAPTER - गुरुत्वाकर्षण EXERCISE - अभ्यास के प्रश्न
40 Videos
- घर्षण BOOK - HC VERMA HINDICHAPTER - घर्षण EXERCISE - अभ्यास के प्रश्न
30 Videos
Similar Questions
चित्र में दिखाई गई परिस्थिति में वस्तु O के प्रतिबिंब का स्थान निर्धारित करें । बिंदु C दोनों माध्यमों की उभयनिष्ठ (COMMON) गोलीय सतह का वक्रता - केंद्र हैं ।
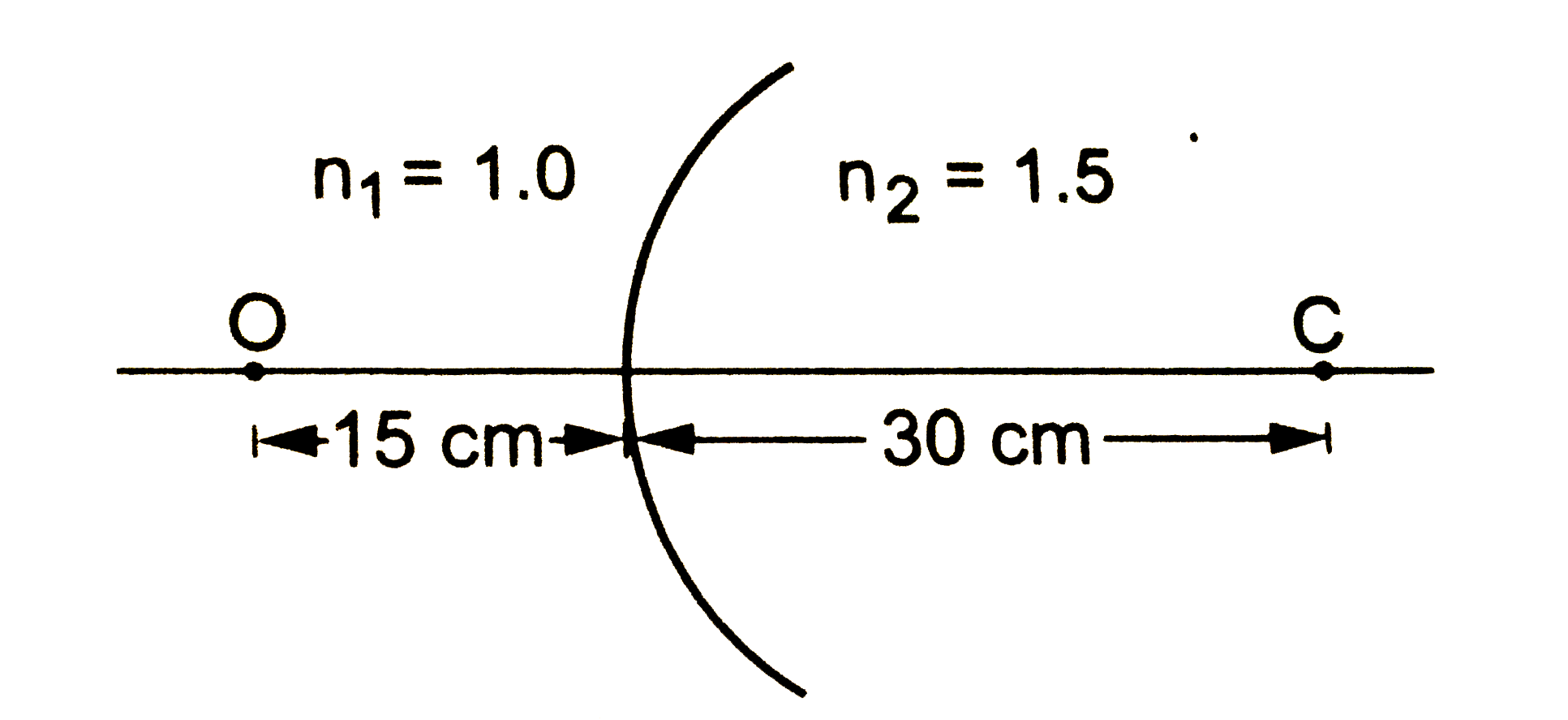
View Solutionएक अपारदर्शी टयूब के अंदर एक लेंस फिट किया हुआ हैं , प्रकाश की एक समानांतर बीम ट्यूब में प्रवेश करती हैं और अपसारी ( divergent) बीम के रुप में ट्यूब के अंदर का लेंस हैं ?
View Solution10 kg द्रव्यमान की दो गोलाकार गेदे एक – दूसरे से 10 cm दूर रखी गई है। इनके बीच लगनेवाले गुरूत्वीय बल ज्ञात करें।
View Solutionएक खुरदरे (rough ) क्षैतिज तल पर फिसल रही वस्तु 4.0m/s2 अवमंदन से गतिशील है|वस्तु तथा तल के बीच गतिज घर्षण गुणांक का मान निकालें|
View Solutionएक बिंदु वस्तु एक काँच जिसका अपवर्तनांक (μs=32) है, से बने 20 सेमी फोकस दूरी वाले उत्तल लेन्स से 30 सेमी की दूरी पर रखी है। वस्तु का अन्तिम प्रतिबिमब अनन्त पर बनेगा यदि
View Solutionनिम्नलिखित प्रश्नों में से किसी एक प्रश्न का उत्तर लगभग 90 शब्दों में लिखिए कवि बैरागी माँ से किस प्रकार के वरदान की अपेक्षा रखते हैं
View Solutionलेंस की क्षमता | लेंस की फोकस दूरी तथा क्षमता में सम्बन्ध
View Solutionलेंस की फोकस दूरी की निर्भरता|लेंस सूत्र तथा संयुग्मी फोकस
View Solutionसंपर्क में रखे दो पतले लेंसों की संयुक्त फोकस दूरी|उत्तल लेंस तथा समतल दर्पण का संयोजन#!#लेंसों के उपयोग
View Solutionप्रकाश - परावर्तन तथा अपवर्तन|गोलीय लेंस से प्रतिबिंब का निर्माण
View Solutionएक द्रव और उसमें नहीं घुलनेवाले ठोस के मिश्रण से अवयवों को पृथक करने की विधियाँ हैं
View SolutionBoard special|प्रकाश - परावर्तन तथा अपवर्तन#!#गोलीय लेस से प्रतिबिंब का निर्माण #!#उत्तल लेंस से प्रतिबिंब का निर्माण
View Solutionउत्तल लेंस से प्रतिबिंब बनने के नियम तथा विभिन्न स्थितियाँ
View Solutionसमाज में वर्ग हैं, श्रेणियाँ हैं। श्रेणियों में परिवार है। समाज की एक बुनियादी इकाई परिवार भी है। समाज की अच्छाई-बुराई । परिवार के माध्यम से व्यक्त होती है। मनुष्य के चरित्र का विकास. 1 परिवार में होता है। बच्चे पलते हैं, उन्हें सांस्कृतिक शिक्षा मिलती है। वे अपनी सारी अच्छाइयाँ-बुराइयाँ वहाँ से लेते हैं। हमारे । साहित्य तथा राजनीति के पास ऐसी कोई दृष्टि नहीं है जो परिवार को लागू हो....
प्रस्तुत पंक्तियाँ किस पाठ से लिया गया है ?
View Solutionसमाज में वर्ग हैं, श्रेणियाँ हैं। श्रेणियों में परिवार है। समाज की एक बुनियादी इकाई परिवार भी है। समाज की अच्छाई-बुराई । परिवार के माध्यम से व्यक्त होती है। मनुष्य के चरित्र का विकास. 1 परिवार में होता है। बच्चे पलते हैं, उन्हें सांस्कृतिक शिक्षा मिलती है। वे अपनी सारी अच्छाइयाँ-बुराइयाँ वहाँ से लेते हैं। हमारे । साहित्य तथा राजनीति के पास ऐसी कोई दृष्टि नहीं है जो परिवार को लागू हो....
समाज की एक बुनियादी इकाई है
View Solutionउत्तल लेंस के द्वारा प्रतिबिंब का निर्माण
View Solution
