एक कण पर दो सरल गतियाँ आरोपित की गई है, जिनमें से एक x - अक्ष की और तथा दुसरी x - अक्ष की और तथा दुसरी x - अक्ष से 45∘ कोण बनाती दिशा में है। इन दो गतियों के समीकरण x=x0sinωt तथा s=s0sinωt है, तो परिणामी गति का आयाम निकालें।
कण की गति के तल को xy-तल माने ।
पहली गति के कारण t समय पर कण की स्थिति , →r1=ˆix0sinωt तथा दुसरी गति के कारण t समय पर कण की स्थिति ,
→r2=ˆi(s0cos45∘)sinωt=ˆj(s0sin45∘)sinωt होगी।
अतः, कण की परिणामी गति,
→r=→r1+→r2=ˆi(x0+s0√2)sinωt+ˆj(s0√2)sinωt.
अतः, x=(x0+s0√2)sinωt तथा y=s0√2sinωt.
अतः, yx=s0√2x0+s0√2
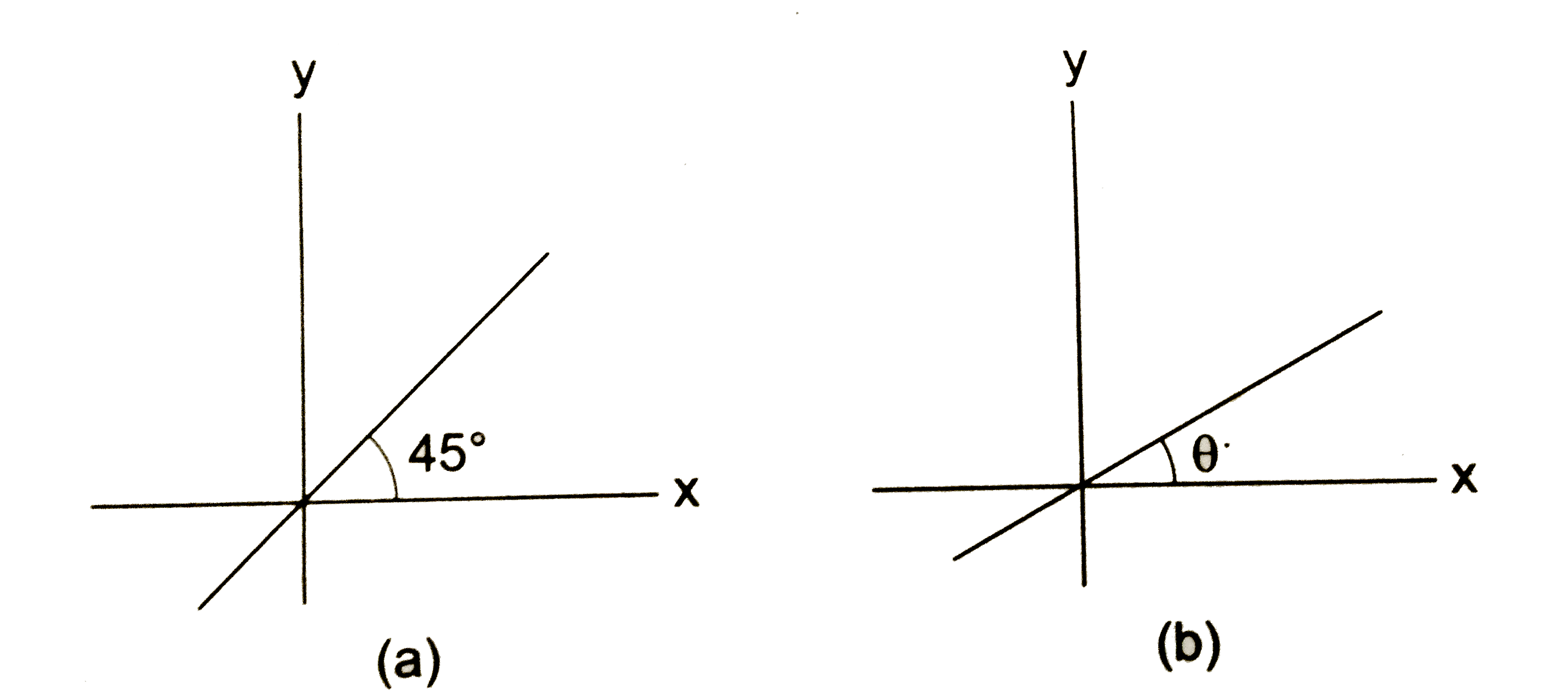
यह समय पर निर्भर नहीं करता। अतः , कण एक सरल रेखा पर गति कर रहा है, जो x - अक्ष से θ कोण बना रही है [चित्र b ], जहाँ
tanθ=yx=s0√2x0+s0.
t समय पर कण की मूलबिंदु से दूरी,
r=√x2+y2=
⎷(x0+s0√2)2+(s0√2)2sinωt
=√x20+s20+√2x0s0sinωt.
अतः, कण का आयाम =√x20+s20+√2x0s0.
Topper's Solved these Questions
- सरल आवर्त गति पर आधारित अन्य गतियाँ Book:HC VERMA HINDIChapter:सरल आवर्त गति पर आधारित अन्य गतियाँ Exercise:विचार हेतु प्रश्न
Explore 2 Videos
- सरल आवर्त गति पर आधारित अन्य गतियाँ Book:HC VERMA HINDIChapter:सरल आवर्त गति पर आधारित अन्य गतियाँ Exercise:सटीक उत्तरवाले प्रश्न I
Explore 10 Videos
- सरल आवर्त गति पर आधारित अन्य गतियाँ Book:HC VERMA HINDIChapter:सरल आवर्त गति पर आधारित अन्य गतियाँ Exercise:अभ्यास के प्रश्न
Explore 8 Videos
- सरल आवर्त गति Book:HC VERMA HINDIChapter:सरल आवर्त गति Exercise:अभ्यास के प्रश्न
Explore 31 Videos
- सरल रेखा में गति Book:HC VERMA HINDIChapter:सरल रेखा में गति Exercise:अभ्यास के प्रश्न
Explore 27 Videos
Similar Questions
एक सरल ढोलक की आवृत्ति 2π√l/g कही जाती है। परन्तु, हवा द्वारा गोलक पर लगते अवमंदन के कारण ढोलक की वास्तविक आवृत्ति इससे कुछ भिन्न होती है। यह वास्तविक आवृत्ति सूत्र द्वारा दी गई आवृत्ति से कम होगी या अधिक ?
View Solutionदो सरल आवर्त गतिओं के संयोजन से
View Solutionएक कण को एकसाथ दो आवर्त गतियाँ प्रदान की जाती है जिसकी दिशाएँ समान है तथा आवर्तकाल भी सामान हैं। एक का आयाम 3.0 cm तथा दूसरे का आयाम 4.0 cm है। परिणामी गति का आवर्तकाल निकालें यदि दोनों के बीच का कलांतर (a)0∘(b)60∘ तथा (c)90∘ हो।
View Solutionमूलबिंदु को मध्यबिंदु बनाकर -अक्ष पर सरल आवर्त गति करते एक कण का आयाम 10cm तथा आवर्तकाल 6s है।t=0 समय पर इसकी स्थिति =5cm है तथा यह अक्ष की धनात्मक दिशा में चल रहा है। t समय पर इसके विस्थापन के लए समीकरण लिखे।t = 4s समय पर कण के त्वरण का परिमाण निकालें
View Solutionएक कण मूलबिंदु से प्रारम्भ कर x - अक्ष पर चलता हुआ x = 20 m पर पँहुचता है और फिर उसी रेखा पर वापस मुड़कर x = -20 m पर आ जाता है | इस पूरी अवधि में कण द्वारा तय की गई दुरी तथा उसका विस्थापन बताएँ |
View Solutionबिंदु A(1,2) से होकर जाने वाली रेखा X-अक्ष के साथ 60∘ का कोण बनाती है तथा x+y=6 को बिंदु P पर काटती है तो AP की लम्बाई ज्ञात कीजिए
View Solutionएक रेखा X- अक्ष तथा Y-अक्ष को बिंदु A तथा B पर मिलती है AB का मध्य बिंदु (x1,y1) है तो रेखा का समीकरण है -
View Solutionएक परवलय की नाभि मूलबिंदु पर है तथा रेखा x=2 परवलय की नियता है , तो परवलय का शीर्ष है
View Solutionसरल रेखा y=2x,X− अक्ष तथा कोटियों x=0 और x=3 से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए ।
View Solutionएक आयत की भुजाओं की लम्बाईयाँ a और b है। यदि उसके एक शीर्ष को मुलबिन्दु तथा x- अक्ष को भुजा a के अनुदिश ले तो आयत की भुजाओं के समीकरण ज्ञात कीजिए।
View Solutionउस सरल रेखा का समीकरण ज्ञात कीजिए जो बिन्दु (1,2) से होकर जाती है और y -अक्ष से ऐसा अन्तः खण्ड काटती है जो कि x -अक्ष पर काटे अन्तः खण्ड को दो गुना है।
View Solutionएक रेखा x- अक्ष से 120∘ तथा y-अक्ष से 60∘ का कोण बनाती है, तो रेखा द्वारा z-अक्ष से बना कोण ज्ञात कीजिए।
View Solutionएक सदिश x- अक्ष v y-अक्ष प्रत्येक के साथ π4 कोण बनाता है, तो z-अक्ष के साथ यह क्या कोण बनाता है ?
View Solutionकोई रेखा x-अक्ष और y-से साथ क्रमशः 60∘ तथा 45∘ के कोण बनाती है। इनके द्वारा घनत्व दिशा में z-अक्ष के साथ कितना कोण बनेगा ?
View Solutionएक अतिपरवलय का केंद्र मूलबिंदु पर है तथा यह बिन्दु (4,2) से होकर जाता है और इसका अनुप्रस्थ (transverse) अक्ष X-अक्ष के अनुदिश है जिसकी लम्बाई 4 है तो इस अतिपरवलय की उत्केन्द्रता (eccentricity) है
View Solutionएक वृत्त X-अक्ष पर एक जीवा काटता है जिसकी लम्बाई 4a है तथा यह वृत्त Y-अक्ष के एक बिन्दु से होकर जाता है जिसकी मूलबिंदु से दुरी 2b है , तो वृत्त के केन्द्र का बिन्दुपथ (locus) है
View Solution

