एक पहिये की त्रिज्या r तथा अपने अक्ष के प्रति जड़त्व आघूर्ण I है। इसे आनंत कोण वाले आनंत तल के ऊपरी सिरे पर क्लैप कर दिया गया है। (चित्र 18,W2)। पहिये की परिधि पर बनी खाँच में एक लंबी रस्सी लपेट दी गई है, जिसके दूसरे सिरे से M द्रब्यगान का एक गुटका बँधा है। गुटका आनंत तल पर बिना घर्षण के फिसल सकता है। t = 0 समय पर पहिये को कोणीय वेग देकर छोड़ दिया जाता है तथा वह चित्र में दिखाए अनुसार दक्षिणावर्ती दिशा में घूमने लगता है। परिणामतः, गुटका आनंत तल पर ऊपर की ओर 'फिसलता है। रुकने के पहले गुटका कितनी दूरी तय करेगा? माने कि रस्सी पहिये पर नहीं फिसलती है
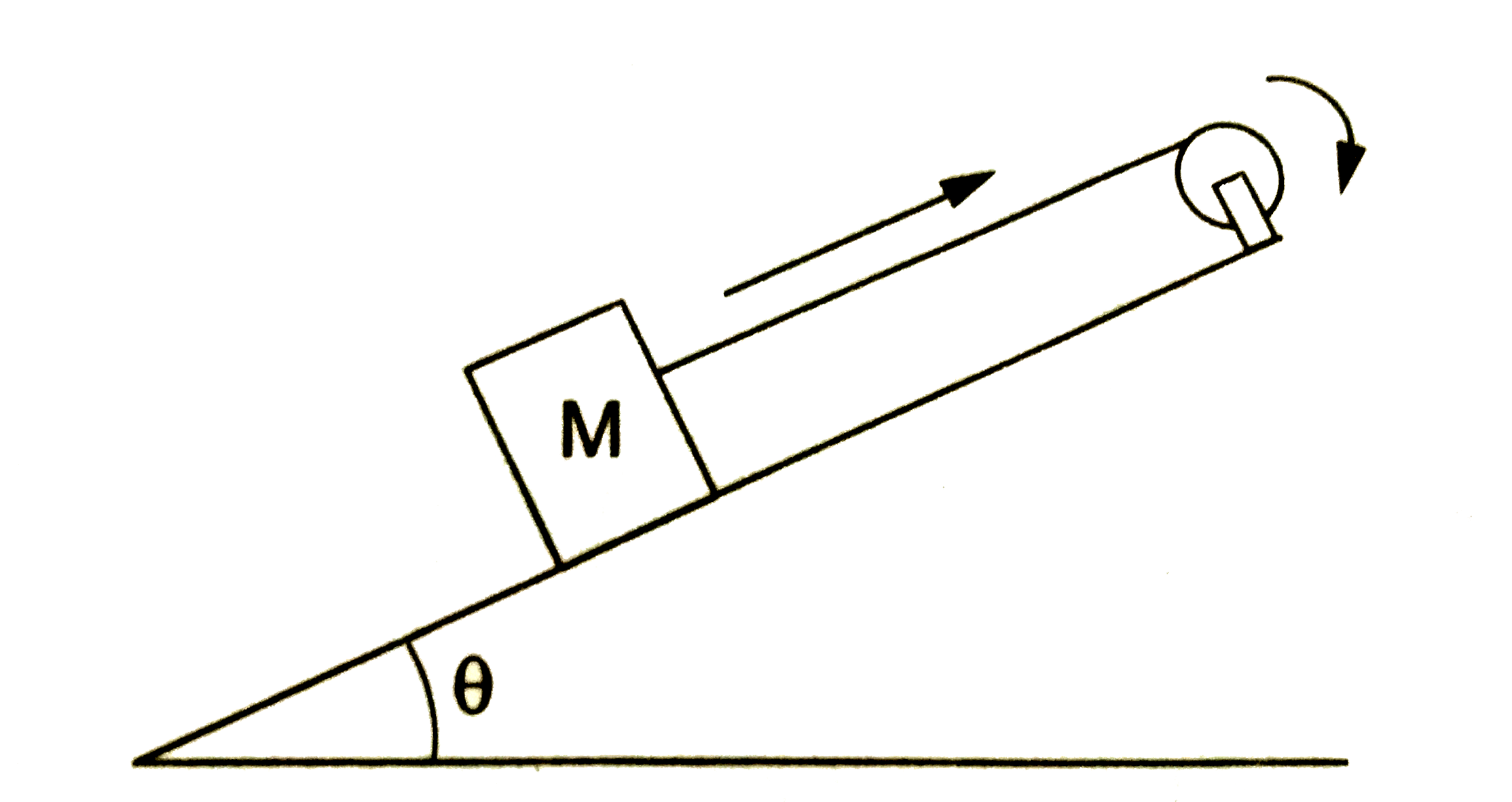
मान ले कि किसी क्षण रस्सी का तनाव T है
पहिये पर रस्सी द्वारा लगते बल का बल-आघूर्ण
वामावर्ती दिशा में होगा तथा उसका कोणीय त्वरण भी वामावर्ती दिशा में होगा
अतः
चूँकि रस्सी पहिये पर नहीं फिसलती है इसका (तथा गुटके का) रेखीय त्वरण
अतः समीकरण (i) से
गुटके के लिए न्यूटन के द्वितीय गति--नियम से
यहाँ तल पर नीचे की ओर धनात्मक दिशा ली गयी है
समीकरण (ii) से
या
यह त्वरण नीचे की ओर है
यदि गुटका तल पर x दुरी चलकर रुके, तो
Topper's Solved these Questions
- बल-आघूर्ण BOOK - HC VERMA HINDICHAPTER - बल-आघूर्ण EXERCISE - विचार हेतु प्रश्न
9 Videos
- बल-आघूर्ण BOOK - HC VERMA HINDICHAPTER - बल-आघूर्ण EXERCISE - सटीक उत्तरवाले प्रश्न I
8 Videos
- बल-आघूर्ण BOOK - HC VERMA HINDICHAPTER - बल-आघूर्ण EXERCISE - अभ्यास के प्रश्न
45 Videos
- प्रत्यास्था BOOK - HC VERMA HINDICHAPTER - प्रत्यास्था EXERCISE - अभ्यास के प्रश्न
13 Videos
- मात्रक और विमाएँ BOOK - HC VERMA HINDICHAPTER - मात्रक और विमाएँ EXERCISE - अभ्यास के प्रश्न
19 Videos
Similar Questions
किसी बस्तु के भार का किसी भी उध्र्व अक्ष के परितः बल-आधूर्ण शून्य होता है। पया यह कथन सदैव सत्य है
View Solutionएक कण का स्थिति वेक्टर →r है और उसपर एक बल →F लग रहा है। मूलबिंदु के परितः इस बल का आघूर्ण →τ है, तब
View Solutionm द्रव्यमान का एक कण μ चाल से क्षैतिज से θ कोण पर प्रक्षेपित किया गया है। जब कण उच्चतम बिंदु पर है, उस समय प्रक्षेपण-बिंदु के परितः इसके भार का बल-आघूर्ण ज्ञात कीजिए
View Solutionअनुप्रस्थ परिच्छेद 4mm2 तथा लंबाई 3 m वाले एक धातु के तार से 10 kg की वस्तु लटकाई गई है। तार के पदार्थ का यंग मॉड्युलस 2.0×1011N/m2 है। ज्ञात करे, (a) प्रतिबल, (b) अनुदैर्ध्य विकृति तथा (c) लंबाई में वृद्धि।
View Solutionनिम्नलिखित राशियों के विमीय सूत्र लिखें।
(a) रेखीय संवेग (b) आवृत्ति (c) दाब
View Solution10 g द्रव्यमान और 50 m/s चाल वाली बंदूक की गोली एक दरवाजे में अंतः स्थापित हो जाती है । दरवाजा 1.0 M चौड़ा है और इसका द्रव्यमान 12 kg है इसके एक सिरे पर कब्जे लगे है और यह इनसे गुजरती एक ऊर्ध्वाधर अक्ष के परितः लगभग बिना घर्षण के घूम सकता है । गोली के दरवाजे में अंतः स्थापन के ठीक बाद इसका कोणीय वेग ज्ञात कीजिए ।
View Solutionएक परवलय की नाभि मूलबिंदु पर है तथा रेखा x=2 परवलय की नियता है , तो परवलय का शीर्ष है
View SolutionL लम्बाई की एक छड़ जिसके सिरे दो परस्पर लम्ब रेखाओं पर स्थित है , फिसलती है । छड़ को 1:2 के अनुपात में विभाजित करने वाले बिंदु का बिन्दुपथ ज्ञात कीजिए ।
View Solutionयदि एक दीर्घवृत्त जिसका केंद्र मूलबिंदु पर है, के दीर्घ कक्ष तथा लघु कक्ष कि लम्बाइयों का अंतर 10 है तथा एक नाभिकेन्द्र (0,5√3) पर है, तो इसके नाभिलम्ब की लम्बाई है
View Solutionएक अतिपरवलय का केंद्र मूलबिंदु पर है तथा यह बिन्दु (4,2) से होकर जाता है और इसका अनुप्रस्थ (transverse) अक्ष X-अक्ष के अनुदिश है जिसकी लम्बाई 4 है तो इस अतिपरवलय की उत्केन्द्रता (eccentricity) है
View Solutionएक वृत्त X-अक्ष पर एक जीवा काटता है जिसकी लम्बाई 4a है तथा यह वृत्त Y-अक्ष के एक बिन्दु से होकर जाता है जिसकी मूलबिंदु से दुरी 2b है , तो वृत्त के केन्द्र का बिन्दुपथ (locus) है
View Solutionयदि एक अतिपरवलय के संयुग्मी अक्ष की लम्बाई 5 है तथा इसकी नाभिको के बीच की दुरी 13 है, तो इस अतिपरवलय की उत्केंद्रता है
View Solutionमाना एक दीर्घवृत्त जिसका दीर्घ -अक्ष, X-अक्ष के अनुदिश है तथा केन्द्र मूलबिंदु पर है, के नाभिलम्ब की लम्बाई 8 है । यदि दीर्घवृत्त की नाभियो के बीच की दुरी, इसके लघु-अक्ष की लम्बाई के समान हो, तो निम्न में से कौन-सा बिन्दु इस पर स्थित है?
View Solutionपरवलय x2=8y पर एक स्पर्श रेखा,जो X-अक्ष की धनात्मक दिशा के साथ कोण θ बनती है, का सभीकरण है
View Solutionएक अतिपरवलय बिन्दुओं (3,2) तथा (-17,12) से गुजरता है और उसका केंद्र मूलबिन्दु पर है तथा अनुप्रस्थ अक्ष x- अक्ष है। अतिपरवलय की अनुप्रस्थ अक्ष की लम्बाई है।
View Solution30 बच्चो की एक कक्षा में सरन शीर्ष से 9 वे रैंक पर है| मनीष सरन से पांच रैंक निचे है| तल से मनीष की रैंक क्या है?
View Solution
