दो द्रव्यमान m तथा M एक नगण्य भार वाली डोरी से बँधे है जो एक स्थिर घिरनी पर से होकर जाती है | घिरनी का अक्ष क्षैतिज है, इसकी त्रिज्या r है तथा अक्ष के प्रति इसका जड़त्व आघूर्ण I है | घिरनी की धुरी पर कोई घर्षण नहीं है तथा डोरी घिरनी पर फिसलती नहीं है | इस पुरे निकाय को स्वतंत्र रूप से गति करने के लिए छोड़ दिए जाता है | जब द्रव्यमान M, h दुरी निचे आता है, उस समय घूर्णन अक्ष के प्रति निकाय का कोणीय संवेग ज्ञात करें |
प्रश्न में दी गई स्थिति चित्र 16.W4 में दिखाई गई है | मान ले कि t समय पर द्रव्यमानो कि चाल υ है | घिरनी कि परिधि के बिन्दुओ का रेखीय वेग भी इस समय υ होगा | अतः, घिरनी का कोणीय वेग ω=υ/r होगा | कोणीय संवेग निकालने के लिए हमें ω तथा υ का मान जानना होगा |
जब द्रव्यमान M, h दुरी से निचे आता है, तो उसकी गुरुत्वीय स्थितिज ऊर्जा Mgh मान से घट जाती है | इस अवधि में द्रव्यमान m,h दुरी ऊपर जाएगा |
अतः, स्थितिज ऊर्जा में कुल कमी,
ΔU=(M−m)gh
होगी |
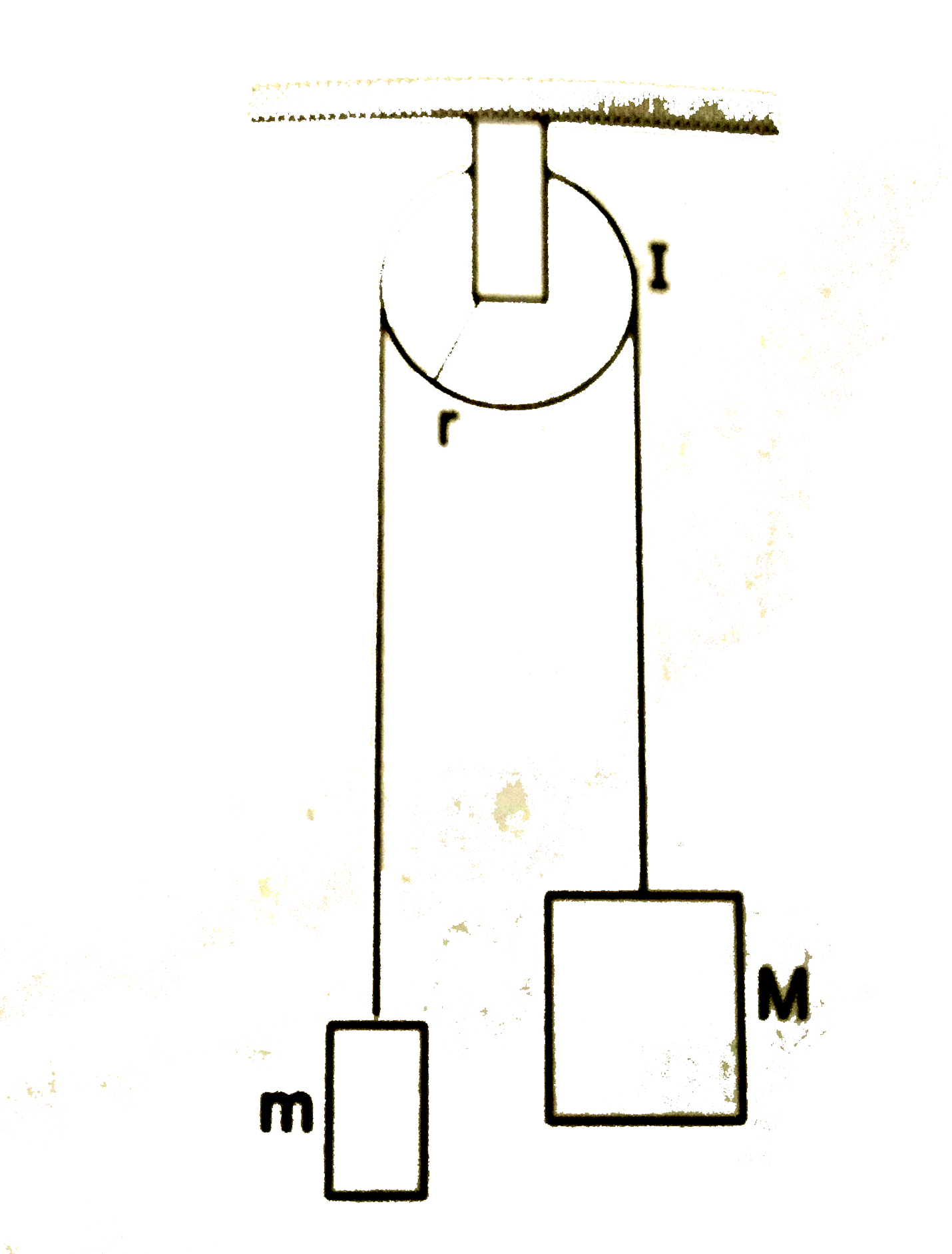
इस समय निकाय की गतिज ऊर्जा,
ΔK=12Mυ2+12mυ2+12I(υr)2.
चूँकि निकाय पर कोई बाहरी बल नहीं लग रहा, कुल यांत्रिक ऊर्जा नहीं बदलेगी | अतः,
(M−m)gh=12(M+m)υ2+12(Ir2)υ2
या υ=
⎷2(M−m)ghM+m+1r2.
M का कोणीय संवेग Mυr,m का कोणीय संवेग mυr तथा घिरनी का कोणीय संवेग Iω=Irυ है | ये सभी कोणीय संवेग एक ही
दिशा में है (चित्र 16.W4 में दक्षिणावर्ती) | अतः, अक्ष के प्रति निकाय का कुल कोणीय संवेग
L=[Mr+mr+Ir]
⎷2(M−m)ghM+m+Ir2
=√2(M−m)(M+m+Ir2)r2gh.
Topper's Solved these Questions
- घूर्णन गतिBOOK - HC VERMA HINDICHAPTER - घूर्णन गतिEXERCISE - अभ्यास
7 Videos
- घूर्णन गतिBOOK - HC VERMA HINDICHAPTER - घूर्णन गतिEXERCISE - विचार हेतु प्रश्न
5 Videos
- घर्षण BOOK - HC VERMA HINDICHAPTER - घर्षण EXERCISE - अभ्यास के प्रश्न
30 Videos
- ज्यामितीय प्रकाशिकी BOOK - HC VERMA HINDICHAPTER - ज्यामितीय प्रकाशिकी EXERCISE - अभ्यास के प्रश्न
40 Videos
Similar Questions
एक इंजन की मोटर अपने अक्ष पर 100 चक्कर/मिनट के कोणीय वेग से घूम रही है | जब मोटर स्विच ऑफ कर दिया जाता है तब वह 15 सेकंड में पूरी तरह रुक जाती है | मोटर का कोणीय त्वरण एकसमान मानते हुए इस 15 सेकंड में इसके द्वारा घुमा हुआ कोण ज्ञात करें |
View Solutionक्या कोई वस्तु शुद्ध स्थानांतरीय गति के साथ शुद्ध घूर्णन गति भी कर सकती है ?
View Solutionएक खुरदरे (rough ) क्षैतिज तल पर फिसल रही वस्तु 4.0m/s2 अवमंदन से गतिशील है|वस्तु तथा तल के बीच गतिज घर्षण गुणांक का मान निकालें|
View Solutionएक अवतल दर्पण की वक्रता-त्रिज्या 40cm है। इससे 30cm पर प्रकाश का एक बिन्दुस्त्रोत रखा हुआ है। प्रतिबिंब की स्थिति ज्ञात करे।
View Solutionएक रेखा X- अक्ष तथा Y-अक्ष को बिंदु A तथा B पर मिलती है AB का मध्य बिंदु (x1,y1) है तो रेखा का समीकरण है -
View Solutionएक कम्पनी दो प्रकार के टेलीफोनों का निर्माण करती है|पहला डोरी युक्त,दूसरा डोरी रहित| डोरी युक्त टेलीफ़ोन के निर्माण में 2 घंटे लगते है तथा रहित डोरी मॉडल के निर्माण में 4 घंटे लगते है| कम्पनी के पास इन प्रतिरूपों के निर्माण के लिए प्रतिदिन अधिक से अधिक 800 कार्य घंटे उपलब्ध है तथा पैकिंग विभाग प्रतिदिन अधिक से अधिक 300 टेलीफ़ोन सेटों को पैक कर सकता है|यदि कम्पनी डोरी युक्त मॉडल को रु 300 में बेचती है तथा डोरी रहित मॉडल को रु 400 में बचती है ,तो उसे प्रत्येक प्रकार के कितने टेलीफ़ोन सेल प्रतिदिन निर्मित करने चाहिए जिससे की उसकी बिक्री अधिकतम हो?
View Solutionउन दो सरल रेखाओं के समीकरण ज्ञात कीजिए जो बिन्दु (0,a) से होकर जाती है तथा जिन पर बिन्दु (2a,2a) से खींचे गए लम्बो की माप a है।
View Solutionउस सरल रेखा का समीकरण ज्ञात कीजिए जो बिन्दु (1,2) से होकर जाती है और y -अक्ष से ऐसा अन्तः खण्ड काटती है जो कि x -अक्ष पर काटे अन्तः खण्ड को दो गुना है।
View Solutionउस सरल रेखा का समीकरण ज्ञात कीजिए जो बिन्दु (a,b,c) से होकर जाती है तथा Y-अक्ष के समान्तरहै।
View Solutionएक 4 सेमी त्रिज्या के वृत्त पर बाह्य बिंदु से दो स्पर्श रेखाओ PA तथा PB कि रचना कीजिए। जहाँ PA तथा PB के मध्य कोण 65∘ है।
View Solutionएक अतिपरवलय बिन्दु P(√2,√3) से होकर जाता है, तथा उसकी नाभियाँ (±2,0) पर है, तो अतिपरवलय के बिन्दु P पर खींची गई स्पर्श रेखा जिस बिन्दु से होकर जाती है, वह है
View Solutionएक त्रिभुज का एक शीर्ष (1,2) पर है तथा इससे होकर जाने वाली दो भुजाओं के मध्य - बिन्दु (−1,1) और (2,3) हैं , तो इस त्रिभुज का केन्द्रक है
View Solutionएक अतिपरवलय का केंद्र मूलबिंदु पर है तथा यह बिन्दु (4,2) से होकर जाता है और इसका अनुप्रस्थ (transverse) अक्ष X-अक्ष के अनुदिश है जिसकी लम्बाई 4 है तो इस अतिपरवलय की उत्केन्द्रता (eccentricity) है
View Solutionसरल रेखा x+2y=1 निर्देशांक अक्षों को A तथा B पर काटती है। मूलबिंदु , A तथा B से होकर जाने वाला वृत्त खींचा गया है , तो मूलबिंदु पर वृत्त की स्पर्श रेखा की A तथा B से लम्बवत दूरियों का योग है
View Solutionएक वृत्त X-अक्ष पर एक जीवा काटता है जिसकी लम्बाई 4a है तथा यह वृत्त Y-अक्ष के एक बिन्दु से होकर जाता है जिसकी मूलबिंदु से दुरी 2b है , तो वृत्त के केन्द्र का बिन्दुपथ (locus) है
View Solutionयदि एक अतिपरवलय के संयुग्मी अक्ष की लम्बाई 5 है तथा इसकी नाभिको के बीच की दुरी 13 है, तो इस अतिपरवलय की उत्केंद्रता है
View Solution
