एक भारी कण को लंबाई l की एक डोरी से लटकाया गया हैं । कण को एक क्षैतिज वेग v0 दिया जाता हैं । डोरी कुछ कोण पर पहुँचकर ढीली हो जाती है तथा कण सिर्फ गुरुत्व के प्रभाव में परवलय पथ में बढ़ता हैं । यदि कण डोरी के स्थिर किनारे पर जा टकराता हैं , तो v0 का मान g तथा l के पदों में निकालें ।
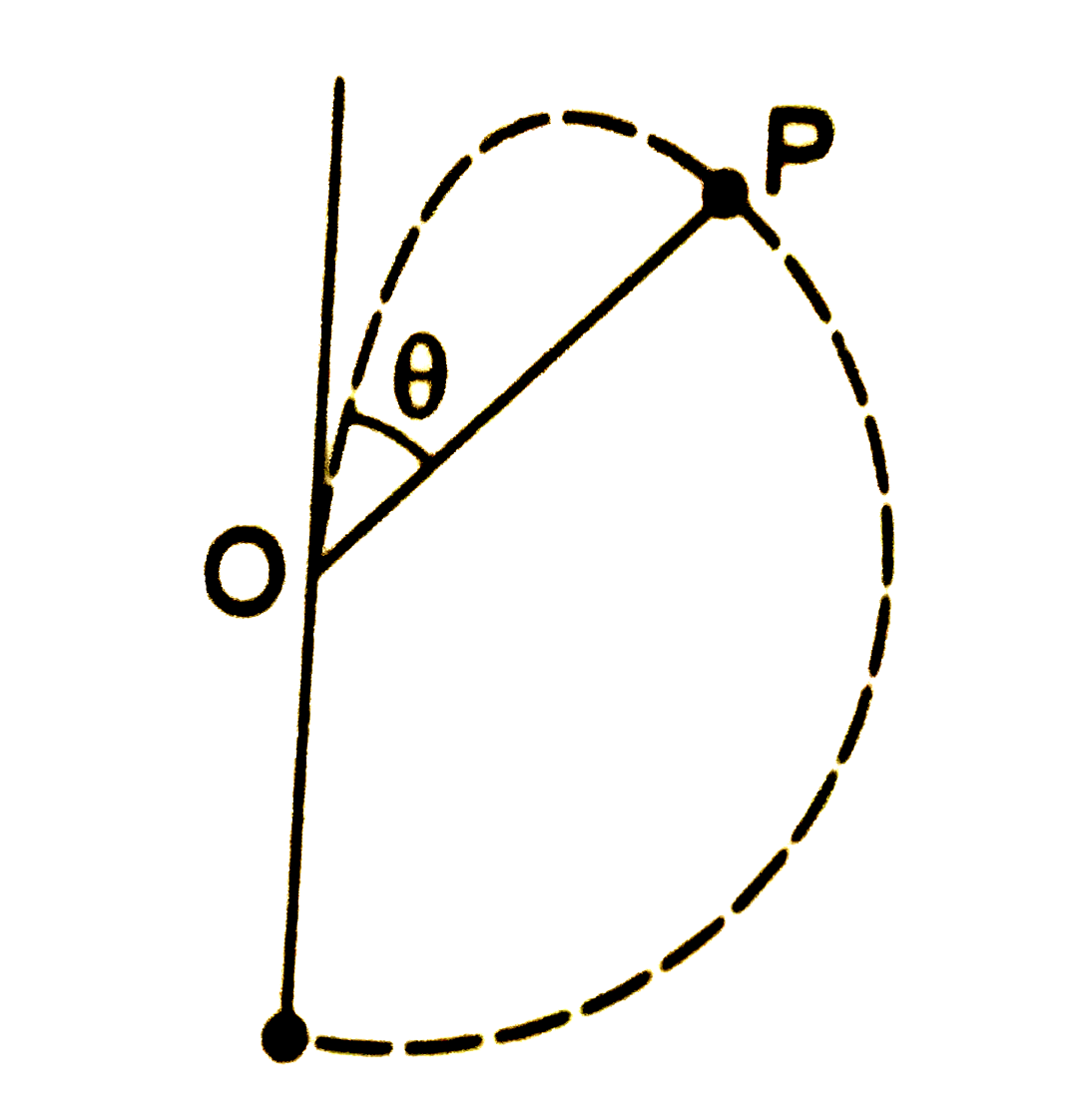
मान लें कि कण जब बिंदु P पर पहुँचता हैं तो डोरी ढीली हो जाती हैं । इस समय ऊर्ध्वाधर से डोरी OP कोण θ बनाती हैं । बिंदु P पर कण के भार mgcosθ होगा । इस समय रस्सी का तनाव शून्य हैं , इसीलिए केंद्र की ओर कुल बल =mgcosθ होगा । चूँकि कण वृत्त में बिंदु P तक गति करता हैं ,
mgcosθ=m(v2l)
या v2=glcosθ, ...(i)
जहाँ v बिंदु P इसकी चाल हैं ।
ऊर्जा - संरक्षण के सिध्दांत से ,
12mv20=12mv2+mgl(1+cosθ)
या v2=v20−2gl(l+cosθ). .....(ii)
समीकरण (i) एंव (ii) सें ,
v20−2gl(1+cosθ)=glcosθ ....(iii)
या v20=gl(2+3cosθ).
अब जब कण परवलय के पथ में जाता हैं तब वह सिर्फ गुरुत्वीय बल के प्रभाव में रहता हैं । P बिंदु पर उसका वेग v , रेखा OP के लंबवत हैं । अतः वेग का क्षैतिज घटक =vcosθ तथा ऊर्ध्वाधर घटक =v0sinθ
P से O तक के विस्थापन के लिए ,
lsinθ=(vcosθ)t
तथा −lcosθ=(vsinθ)t−12 gt2
या −lcosθ=(vsinθ)(lsinθvcosθ)−12g(lsinθvcosθ)2
या −cos2θ=sin2θ−12g(lsin2θv2cosθ)2
या −cos2θ=1−cos2θ−12glsin2θglcos2θ [समीकरण (i) से ]
या 1=12tan2θयाtanθ=√2. समीकरण (iii) से , v0=[gl(2+√3)]12.
Topper's Solved these Questions
- स्थितिज ऊर्जा एंव ऊर्जा - सरंक्षण का सिध्दांत BOOK - HC VERMA HINDICHAPTER - स्थितिज ऊर्जा एंव ऊर्जा - सरंक्षण का सिध्दांत EXERCISE - अभ्यास
4 Videos
- स्थितिज ऊर्जा एंव ऊर्जा - सरंक्षण का सिध्दांत BOOK - HC VERMA HINDICHAPTER - स्थितिज ऊर्जा एंव ऊर्जा - सरंक्षण का सिध्दांत EXERCISE - विचार हेतु प्रश्न
6 Videos
- सरल रेखा में गति BOOK - HC VERMA HINDICHAPTER - सरल रेखा में गति EXERCISE - अभ्यास के प्रश्न
27 Videos
Similar Questions
दो आवेशित कण A तथा B एक दूसरे को k/r2 बल से प्रतिकर्षित करते हैं , जहाँ k एक अचर राशि हैं तथा r उनके बीच की दूरी हैं । कण Aको एक स्थान पर जड़कर रखा गया हैं । कण B , जिसका द्रव्यमान m हैं , A से r0 दूरी से स्थिर अवस्था से छोड़ दिया जाता हैं । कणों पर सिर्फ उनके बीच के प्रतिकर्षण बल को प्रभावी मानें। (a) इन कणों की विद्युतीय स्थितिज ऊर्जा में परिवर्तन ज्ञात करें जब कण B की दूरी A से काफी अधिक हो जाती हैं । (b) इस स्थिति में B की चाल बताएँ ।
View Solutionजब आप जमीन से एक बॉक्स उठाकर आलमारी में रखते हैं तो बॉक्स की स्थितिज ऊर्जा में वृध्दि होती हैं , किंतु इसकी गतिज ऊर्जा में कोई परिवर्तन नहीं होता । क्या यह ऊर्जा - सरंक्षण के सिध्दांत का उल्लंघन नहीं हैं ?
View Solutionएक कण मूलबिंदु से प्रारम्भ कर x - अक्ष पर चलता हुआ x = 20 m पर पँहुचता है और फिर उसी रेखा पर वापस मुड़कर x = -20 m पर आ जाता है | इस पूरी अवधि में कण द्वारा तय की गई दुरी तथा उसका विस्थापन बताएँ |
View Solutionद्रव्यमान m के एक कण को गति y=ut+12gt2 से वर्णित है । उस कण पर लगने वाले बल को ज्ञात करो ।
View Solutionएक 5 मीटर का लड़का 2 मीटर त्रिज्या के क्षैतिज व्रत में एक प्रथर को डोरी से बांधकर, एकसमान्य चाल से घुमा रहा है व्रत की स्पर्श रेखा के अनुदिश चलते हुवे पृथ्वी पर 10 मीटर की क्षितिज दुरी पर गिरता है वृतीय गति में पत्थर पर कार्यरत अभिक्रिया त्वरण का मान ज्ञात कीजिय ( g = 10 मीटर/सेकण्ड2)|
View Solutionएक कम्पनी दो प्रकार के टेलीफोनों का निर्माण करती है|पहला डोरी युक्त,दूसरा डोरी रहित| डोरी युक्त टेलीफ़ोन के निर्माण में 2 घंटे लगते है तथा रहित डोरी मॉडल के निर्माण में 4 घंटे लगते है| कम्पनी के पास इन प्रतिरूपों के निर्माण के लिए प्रतिदिन अधिक से अधिक 800 कार्य घंटे उपलब्ध है तथा पैकिंग विभाग प्रतिदिन अधिक से अधिक 300 टेलीफ़ोन सेटों को पैक कर सकता है|यदि कम्पनी डोरी युक्त मॉडल को रु 300 में बेचती है तथा डोरी रहित मॉडल को रु 400 में बचती है ,तो उसे प्रत्येक प्रकार के कितने टेलीफ़ोन सेल प्रतिदिन निर्मित करने चाहिए जिससे की उसकी बिक्री अधिकतम हो?
View Solutionएक कण y=x2+2x से साथ-साथ चलता है। व्रक के किस बिंदु पर x तथा y निर्देशांक समान दर से परिवर्तित हो रहे है ?
View Solutionयदि एक त्रिभुज , जिसका एक शीर्ष परवलय के शीर्ष परवलय y2+4(x−a2)=0 तथा अन्य दोनों शीर्ष y-अक्ष तथा परवलय के प्रतिच्छेदन बिंदुओं पर हैं , का क्षेत्रफल 250 वर्ग इकाई है , तो 'a' का एक मान है
View Solutionयदि एक कण पर क्रिया करते हुए तीन बल संतुलन में हैं। पहले दो के बीच का कोण 90∘, ... दूसरे और तीसरे के बीच का कोण 120∘ हैं, तो बलों का अनुपात ज्ञात कीजिए।
View Solutionएक कण पर लगे समान परिमाण वाले तीन बल संतुलन में हैं, तो उनके बीच व कोण _____ होगा।
View Solutionआवेशित कण की एक समान चुंबकीय क्षेत्र में गति
View Solutionगंदले जल को एक पात्र में लेकर कुछ देर के लिए स्थिर रख देते हैं। अशुद्धियाँ पात्र की तल पर बैठ जाती है। इसके बाद स्वच्छ जल को अलग कर लेते हैं। इस प्रक्रिया को ..... कहते हैं।
View Solutionसमाज में वर्ग हैं, श्रेणियाँ हैं। श्रेणियों में परिवार है। समाज की एक बुनियादी इकाई परिवार भी है। समाज की अच्छाई-बुराई । परिवार के माध्यम से व्यक्त होती है। मनुष्य के चरित्र का विकास. 1 परिवार में होता है। बच्चे पलते हैं, उन्हें सांस्कृतिक शिक्षा मिलती है। वे अपनी सारी अच्छाइयाँ-बुराइयाँ वहाँ से लेते हैं। हमारे । साहित्य तथा राजनीति के पास ऐसी कोई दृष्टि नहीं है जो परिवार को लागू हो....
समाज की एक बुनियादी इकाई है
View SolutionRecap|यदि आवेशित कण एकसमान चुम्ब्कीय क्षेत्र में किसी कोण पर गतिमान हो|प्रश्न|Summary
View Solutionएक लाल ठोस जल में अविलेय है। हालांकि, जल में कुछ KI को मिलाने पर यह विलेय हो जाता है। एक परखनली में लाल ठोस को गर्म करने पर कुछ बैंगनी रंग के धूम मुक्त होते हैं और परखनली के ठंडे भागों पर एक धातु की बूंदें दिखाई देती हैं। लाल ठोस है -
View Solution1.0 mg के द्रव्यमान वाले एक कण का वेग 3600 km/h है। कण के तरंग दैर्ध्य की गणना कीजिए।
View Solution
