चित्र में दिखाए अनुसार तीन गुटके $m_{1}, m_{2}$ एवं $m_{3}$ आपस में डोरियों द्वारा जुड़े हुए हैं | सभी सतहें घर्षणरहित हैं तथा डोरियों एवं घिरनियों के भार नगण्य हैं | गुटके $m_{1}$ का त्वरण ज्ञात करें |

Video Solution

Text Solution

Verified by Experts

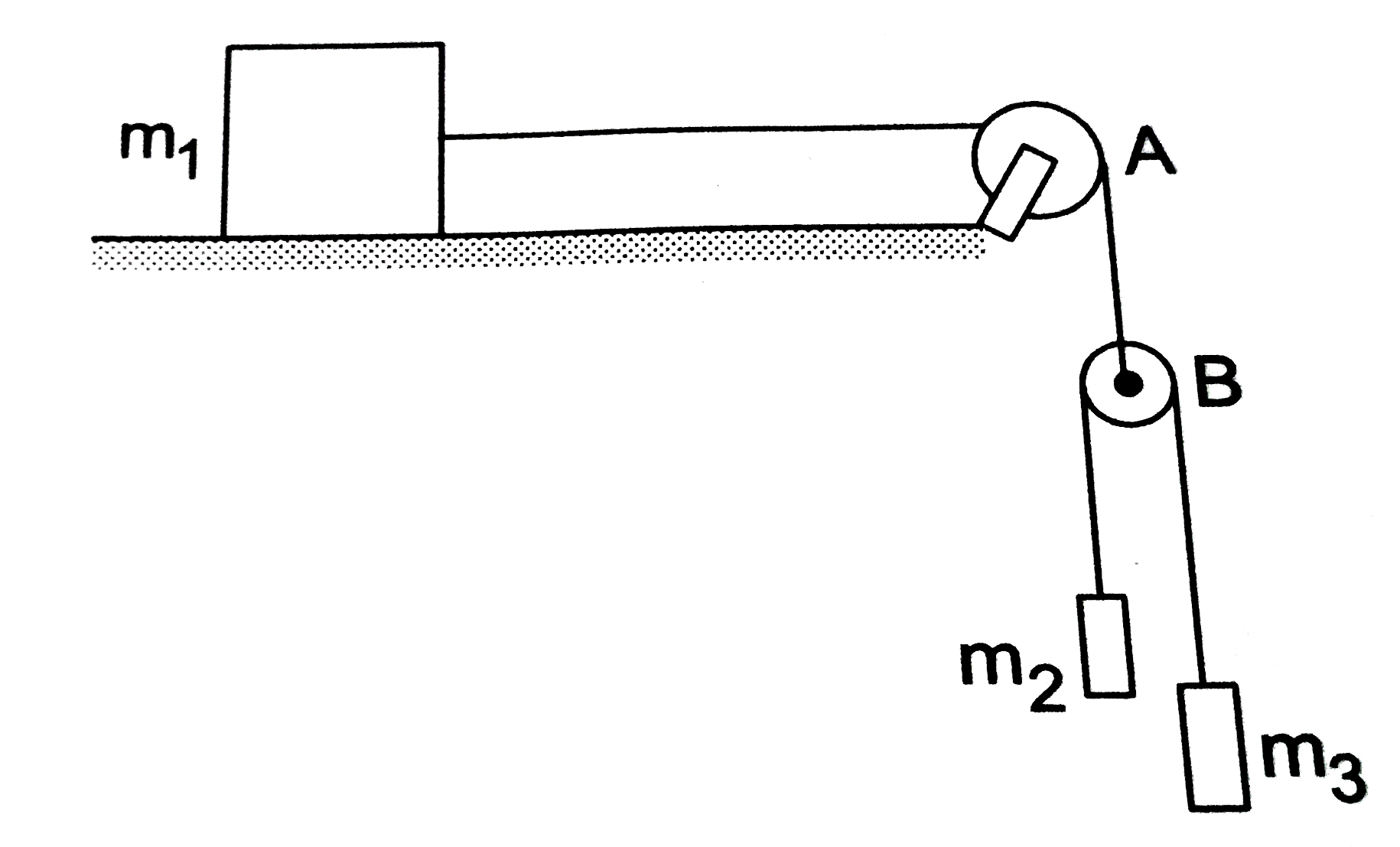
मान लें कि $m_{1}$ का त्वरण दाहिनी ओर $a_{0}$ है | घिरनी B का भी त्वरण $a_{0}$ ही होगा | ऐसा इसलिए कि $m_{1}$ से घिरनी B तक की डोरी की लंबाई निश्चित है |
$a_{B, ground} = a_{0} .$
गुटके $m_{2}$ तथा $m_{3}$ को जोड़नेवाली डोरी की लंबाई भी निश्चित है | अत:, घिरनी B से $m_{2}$ की दूरी जितनी घटेगी (या बढ़ेगी) उतनी ही B से $m_{3}$ की दूरी बढ़ेगी (या घटेगी) | अत:, घिरनी B के सापेक्ष $m_{2}$ का जितना त्वरण ऊपर की ओर होगा उतना ही $m_{3}$ का नीचे की ओर होगा | इस राशि को a मानें | घिरनी B के सापेक्ष $m_{2}$ का त्वरण ऊपर की ओर मानते हुए,
$m_{2}$ का त्वरण ऊपर की ओर मानते हुए,
$m_{2}$ का जमीन के सापेक्ष त्वरण
$= m_{2}$ का घिरनी के सापेक्ष त्वरण + घिरनी का जमीन के सापेक्ष त्वरण
$= a_{0} - a$ नीचे की ओर |
इसी प्रकार, $m_{3}$ का जमीन के सापेक्ष त्वरण $= a_{0} + a$ नीचे की ओर |
मान लें की $m_{1}$ से B तक की डोरी में तनाव = T और $m_{2}$ तथा $m_{3}$ को जोड़ने वाली डोरी में तनाव = T'.
घिरनी B पर न्यूटन के गति-नियम का उपयोग करने पर,
$2 T' - T = 0 या T' = \frac{T}{2} .$
$m_{1}$ पर न्यूटन के गति-नियम का उपयोग करने पर,
$T = m_{1} a_{0} . ... (i)$
$m_{2}$ पर गति-नियम का उपयोग करने पर,
$m_{2} g - T' = m_{2} (a_{0} - a)$
या $m_{2} g - \frac{T}{2} = m_{2} (a_{0} - a) . ... (i i)$
$m_{3}$ पर गति-नियम का उपयोग करने पर,
$m_{3} g - \frac{T}{2} = m_{3} (a_{0} + a) . ... (i i i)$
$a_{0}$ का मान निकालने के लिए इन तीनों से T तथा a को हटाना होगा | समीकरण (i) से T का मान लेकर समीकरण (ii) तथा (iii) में रखने पर,
$a_{0} - a = \frac{m_{2} g - \frac{m_{1} a_{0}}{2}}{m_{2}} = g - \frac{m_{1} - a_{0}}{2 m_{2}}$
तथा $a_{0} + a = \frac{m_{3} g - \frac{m_{1} a_{0}}{2}}{m_{3}} = g - \frac{m_{1} a_{0}}{2 m_{3}}$
इन्हें जोड़ने पर, $2 a_{0} = 2 g - \frac{m_{1} a_{0}}{2} (\frac{1}{m_{2}} + \frac{1}{m_{3}})$
या $a_{0} = g - \frac{m_{1} a_{0}}{4} (\frac{1}{m_{2}} + \frac{1}{m_{3}})$
या $a_{0} [1 + \frac{m_{1}}{4} (\frac{1}{m_{2}} + \frac{1}{m_{3}})] = g$
या $a_{0} = \frac{g}{1 + \frac{m_{1}}{4} (\frac{1}{m_{2}} + \frac{1}{m_{3}})} .$

|

Updated on:21/07/2023

Class 12 PHYSICS न्यूटन के गति-नियम

Topper's Solved these Questions

Similar Questions

HC VERMA HINDI-न्यूटन के गति-नियम -अभ्यास के प्रश्न

Home
Ask Doubt
Profile