एक घर्षणरहित आनत तल के किनारे पर बँधी एक चिकनी घिरनी पर से एक नगण्य भार वाली रस्सी जाती है (चित्र) | रस्सी के एक छोर से m1 द्रव्यमान की एक वस्तु बँधी है जो आनत तल पर फिसल सकती है तथा दूसरे छोर से m2 द्रव्यमान की एक वस्तु बँधी है जो ऊर्ध्वाधर दिशा में लटक रही है | दोनों वस्तुएँ स्थिर हैं | आनत तल का क्षैतिज से कोण θ तथा तल द्वारा m1 द्रव्यमान वाली वस्तु पर लगता बल निकालें |
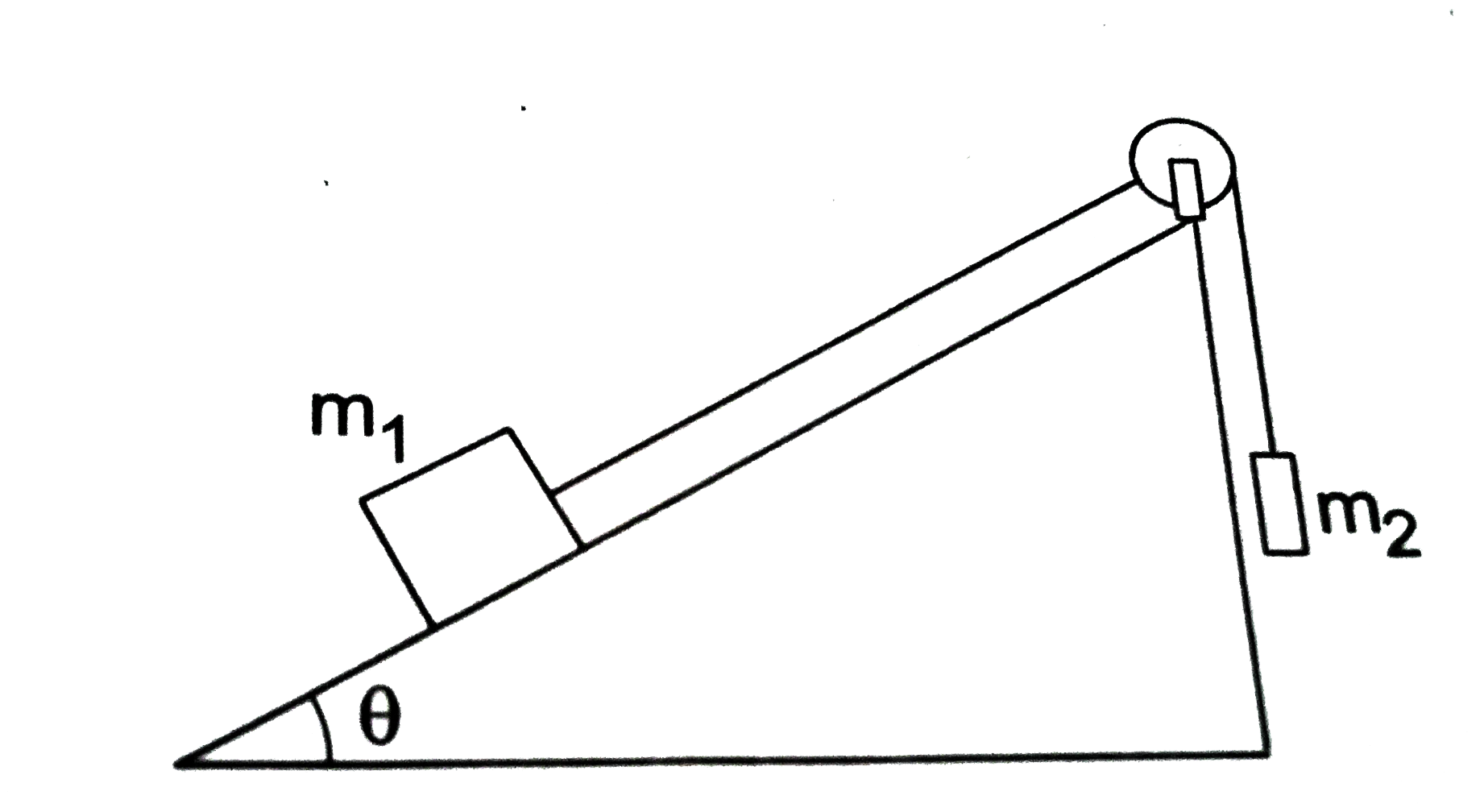
चित्र में हमने दोनों वस्तुओं पर लगते बलों को दिखाया है | पहले m2 द्रव्यमान बलि वस्तु को अपनी संहति मानें | इसपर लगते बल हैं,
(i) धरती द्वारा m2g, निचे की ओर ,
(ii) डोरी द्वारा T1, ऊपर की ओर |
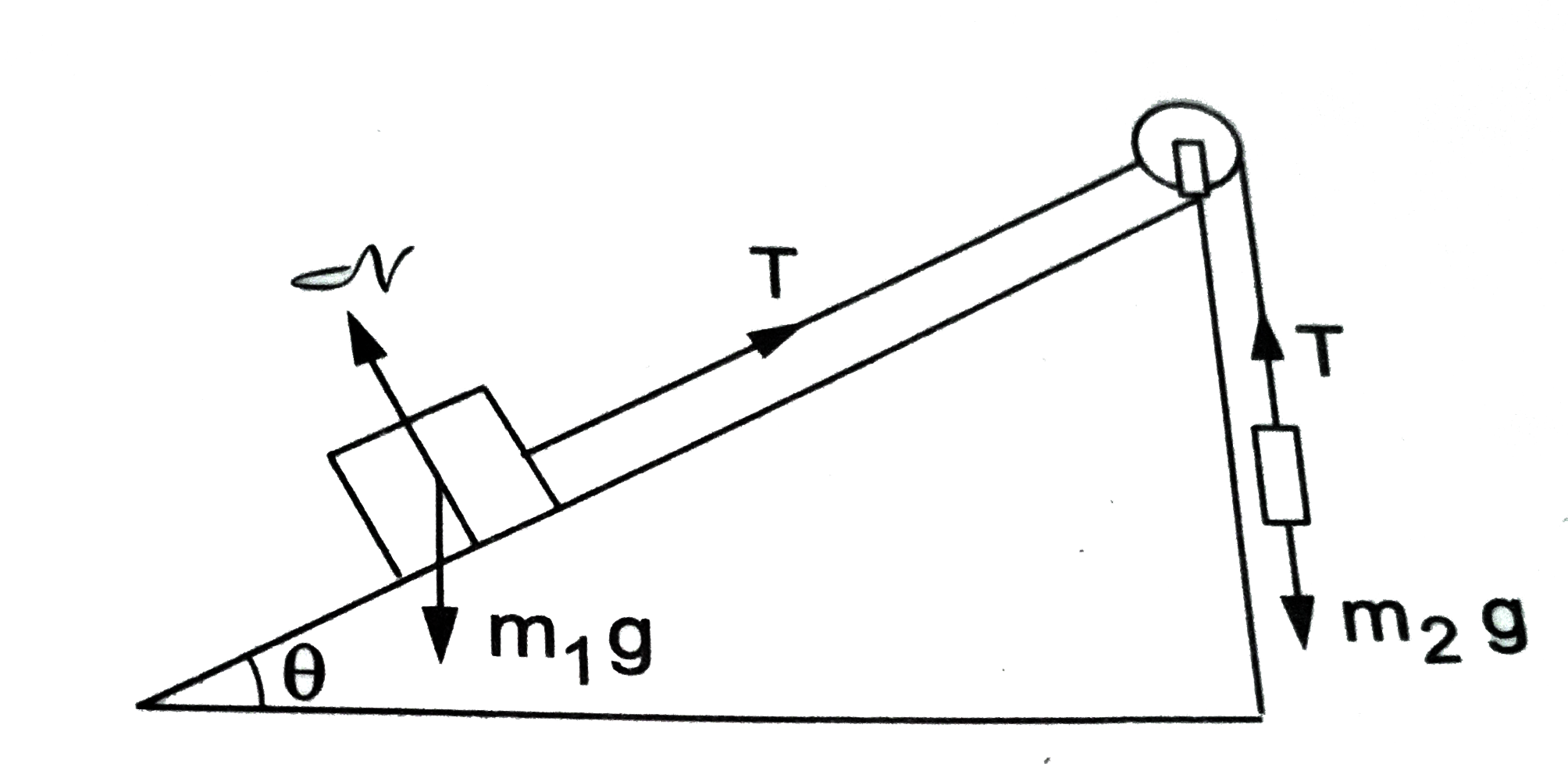
चूँकि वस्तु संतुलन में है, अत :
T=m2g. ...(i)
अब m1 द्रव्यमान वाली वस्तु को संहति मानें | इसपर लगते बल हैं
(i) धरती द्वारा m1g, निचे की ओर ,
(ii) डोरी द्वारा T, डोरी की दिशा में ,
(iii) तल द्वारा N, तल के लंबवत |
पूरी डोरी के बीच कहीं कोई द्रव्यमान नहीं है, न ही डोरी पर कोई घर्षण बल है, इसलिए पूरी डोरी में तनाव एकसमान ही होगा | इसलिए डोरी के दोनों सिरों पर हमने समान तनाव T लिया है |
चूँकि वस्तु संतुलन में है, इन बलों का योग शून्य होगा |
आनत तल की समानांतर दिशा में घटक लेने पर,
T=m1gcos(π2−θ)=m1gsinθ. ...(ii)
आनत तल की लंबवत दिशा में घटक लेने पर,
N=m1gcosθ. ...(iii)
समीकरण (i) और (ii) से,
m2g=m1gsinθ
या sinθ=m2m1
या θ=sin−1(m2m1).
अब θ का मान समीकरण (iii) में रखने पर,
N=m1g√1−(m2/m1)2.
Topper's Solved these Questions
- न्यूटन के गति-नियम BOOK - HC VERMA HINDICHAPTER - न्यूटन के गति-नियम EXERCISE - अभ्यास 8.1
3 Videos
- न्यूटन के गति-नियम BOOK - HC VERMA HINDICHAPTER - न्यूटन के गति-नियम EXERCISE - अभ्यास 8.2
3 Videos
- ध्वनि तरंगो का अध्यारोपणBOOK - HC VERMA HINDICHAPTER - ध्वनि तरंगो का अध्यारोपणEXERCISE - अभ्यास के प्रशन
39 Videos
- प्रकाश का विवर्तन BOOK - HC VERMA HINDICHAPTER - प्रकाश का विवर्तन EXERCISE - अभ्यास के प्रश्न
6 Videos
Similar Questions
चित्र में एक मनुष्य एक रस्सी के सहारे M द्रव्यमान के एक गुटके को निचे उतार रहा है । वह रस्सी इस तरह जाने देता है कि गुटके का त्वरण निचे की ओर a होता है ।
रस्सी के निचले सिरे पर उसमें तनाव निकालें ।
View Solutionएक घर्षणरहित घिरनी छत से एक क्लैम्प द्वारा टाँगकर रखी गई है । घिरनी से होकर जाती एक नगण्य भार वाली डोरी के सिरों से दो गुटके A तथा B, जिनके द्रव्यमान क्रमश : m1 तथा m2 हैं, बाँधकर लटकाए गए हैं ।
दोनों गुटकों के त्वरणों में संबंध बताएँ ।
View Solutionक्विंक की उपकरण में जब खिसकनेवाली नली को 2.50 cm खिसका दिया जाता है तो धवनि की त्रीवता अदिक्तम से न्यूनतम हो जाती है धवनि की आवर्ती निकले हवा में धवनि की चल =340 m/s
View Solution5.0 cm चौड़ाई की एक लम्बी स्लिट पर माइक्रोवेव तरंगें लम्बवत पड़ रही हैं। यदि पहली अदीप्त फ्रिंज θ=30∘ पर बन रही हो, तो माइक्रोवेव का तरंगदैर्घ्य निकालें।
View Solutionएक व्यक्ति के एक कदम आगे चलने की प्रायिकता 0.4 तथा एक कदम पीछे हटने की प्रायिकता 0.6 है। इस बात की क्या प्रायिकता है की ग्यारह कदमो के पशचात वह व्यक्ति शुरुआती बिन्दु से एक कदम दूर है?
View Solutionआनत तल पर वस्तु की गति
View Solutionरेखा 4x−3y+2=0 के समांतर रेखाएं खींची गई है जो मूलबिंदु 35 से की दुरी पर है, तो निम्न में से कौन-सा एक बिंदु इनमे से किसी रेखा पर स्थित है?
View Solutionएक वृत्त X-अक्ष पर एक जीवा काटता है जिसकी लम्बाई 4a है तथा यह वृत्त Y-अक्ष के एक बिन्दु से होकर जाता है जिसकी मूलबिंदु से दुरी 2b है , तो वृत्त के केन्द्र का बिन्दुपथ (locus) है
View Solutionआनत घर्षण वाले तल पर वस्तु की गति -1
View Solutionआनत घर्षण वाले तल पर वस्तु की गति -2
View Solutionघर्षण कोण | समतल सतह पर वस्तु की गति | आनत तल पर वस्तु की गति
View Solutionएक थैले में 3 सफेद और 5 काली गेंदें हैं। थैले के अंदर से बिना देखे एक गेंद निकाली जाती है।
(a) एक सफेद गेंद प्राप्त करने की प्रायिकता क्या है?
(b) एक काली गेंद प्राप्त करने की प्रायिकता क्या है?
View Solutionएक तीन साल के बच्चे से किसी भी ऐसे विषय पर बातचीत की जा सकती है, जो उसके दायरे में आता हो।
View Solution30 बच्चो की एक कक्षा में सरन शीर्ष से 9 वे रैंक पर है| मनीष सरन से पांच रैंक निचे है| तल से मनीष की रैंक क्या है?
View Solutionएक 5 kg द्रव्यमान वाली वस्तु पर 2s के लिये एक नियत बल कार्यरत होता है। यह वस्तु के वेग को 3m/s से बढा 7m/s कर देता है। लगाये गये बल की मात्रा ज्ञात करें
View Solutionएक वस्तु पूर्व दिशा की ओर 30 मी/से के वेग से जा रही है। 10 सेकण्ड के बाद यह वस्तु 40 मी/से के वेग से उत्तर की ओर गति करती है। वस्तु का औसत त्वरण है-
View Solution
