एक गेंद को जमीन से 19.6 मीटर ऊँचे बिंदु से गिराया जाता है | इस बिंदु को मूलबिंदु ले तथा नीचे की दिशा को x - अक्ष लें | यह जमीन से टकराकर ऊपर की दिशा में उतनी ही दुरी तक जाती है, जहाँ से इसे गिराया गया तथा | a−t,v−t तथा x -t के लिए प्रश्न में दी गई अवधि के लिए लगभग ग्राफ खींचे |गेंद जितनी देर जमीन से सम्पर्क में रहती है उसे नगण्य माने |
गेंद जब जमीन के साथ सम्पर्क में आती है तो उसका वेग नीचे की ओर से बदलकर ऊपर की ओर हो जाता है | अतः , इस अवधि में इसका त्वरण g से अलग है | इसलिए हमे नीचे आने के समय की गति और ऊपर जाने के समय की गति के लिए अलग - अलग समीकरण लिखना होगा |
a - t : नीचे की गति के लिए a=g=9.8m/s2
ऊपर की गति के लिए , a=g=9.8m/s2
त्वरण - समय ग्राफ नीचे के चित्र में दिखाया गया है | हमने t=2s पर एक खली जगह (gap ) छोड़ दी है | t=2s पर जमीन से सम्पर्क के समय त्वरण g नहीं है , इसलिए यह खली जगह (gap ) छोड़ी गई है |
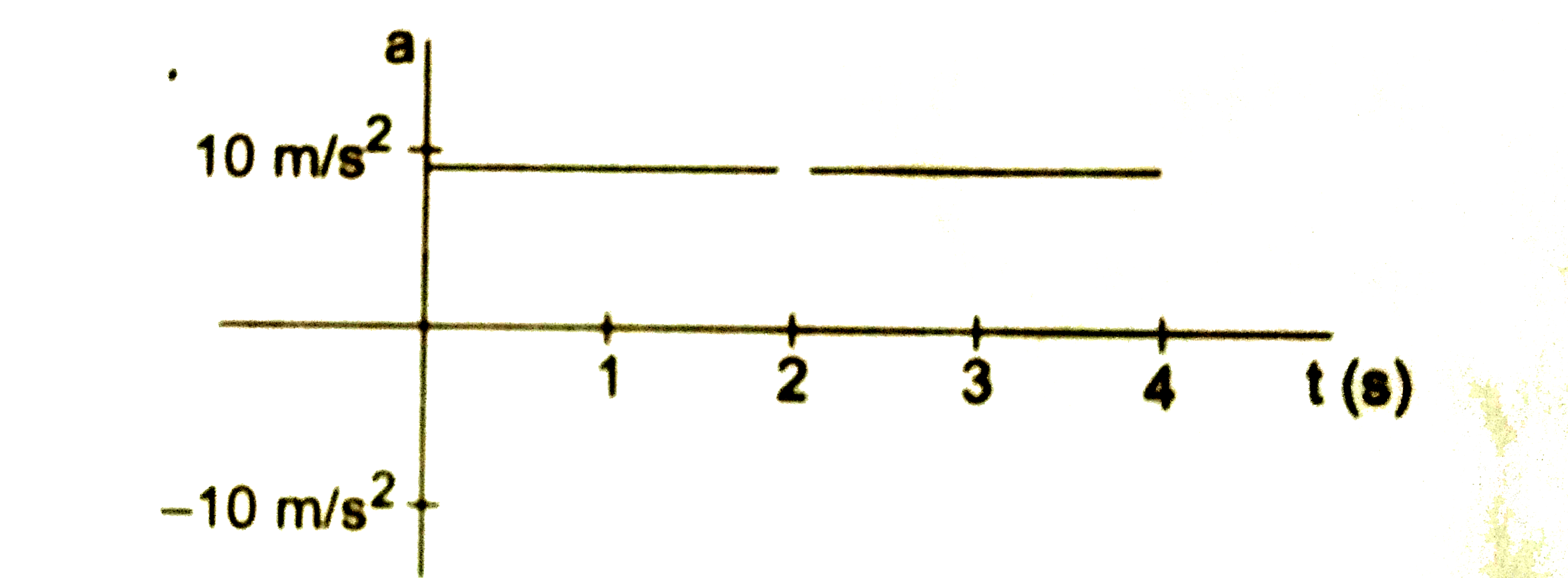
v-t : पहले 2 सेकंड के लिए, v=u+at=(9.8m/s2)t.
t=0,v=0
t=1s,v=9.8m/s
t=2s,v=19.6m/s
इस समय गेंद की दिशा पलट जाती है और वह ऊपर की ओर जाने लगती है | चूँकि गेंद ऊपर की ओर भी उतनी ही दुरी 19.6 मीटर तक पँहुचती है, t = 2s पर पलटने के बाद गेंद का वेग ऊपर की ओर 19.6 m//s होगा | इसके बाद प्रति सेकंड गेंद की चाल 9.8 m//s घटती जायेगी | अतः,
t=2s,v=−19.6m/s
t=3s,v=−9.8m/s
t=4s,v=0m/s
वेग - समय ग्राफ चित्र में दिखाया गया है |
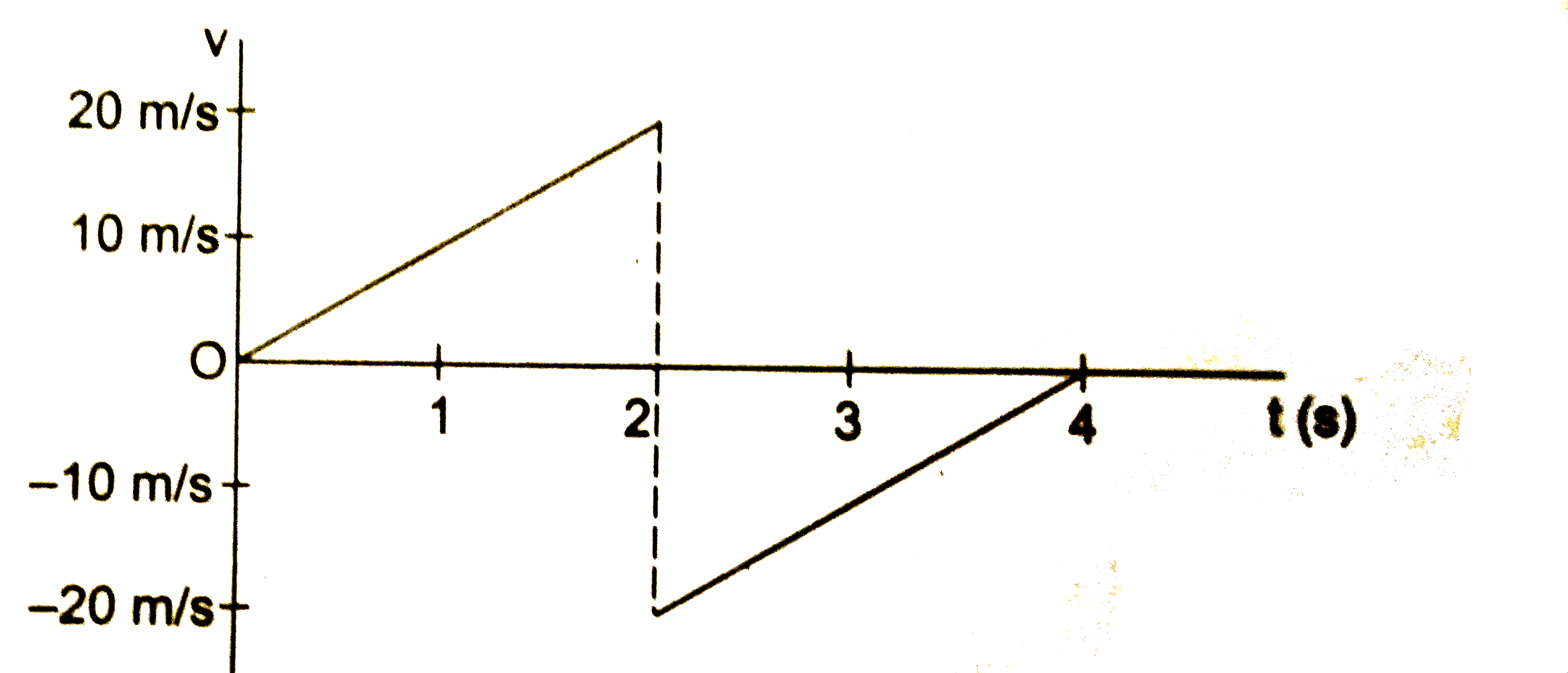
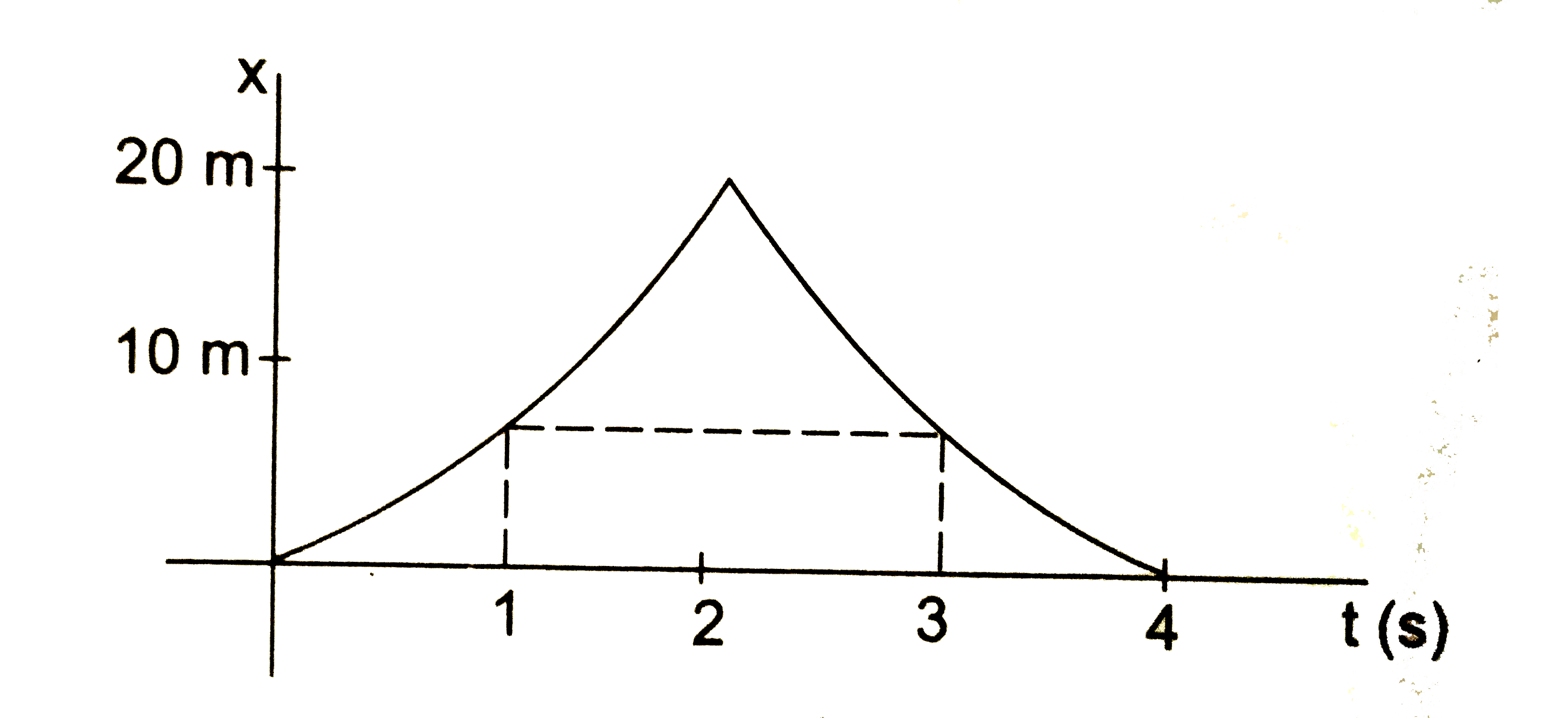
x -t : नीचे की गति के लिए, x=12at2=12×(9.8m/s2)t2
अतः t=0,x=0
t=1s,x=4.9m
t=2s,x=19.6m
t=2s के बाद उसका वेग −19.6m/s हो जाता है | त्वरण =9.8m/s2 , अतः इसके 1 s बाद गेंद का विस्थापन
=ut+12at2=(−19.6m/s)(1s)+(4.9m/s2)(1s2)
=−14.7m
इस समय मूलबिंदु से उसकी स्थिति
=19.6m−14.7m=4.9m
अतः, t=3s पर x=4.9m
इसी तरह t=4s पर x=0
चित्र में x -t ग्राफ दिखाया गया है |
Topper's Solved these Questions
- सरल रेखा में गति BOOK - HC VERMA HINDICHAPTER - सरल रेखा में गति EXERCISE - विचार हेतु प्रश्न
4 Videos
- सरल रेखा में गति BOOK - HC VERMA HINDICHAPTER - सरल रेखा में गति EXERCISE - सटीक उत्तरवाले प्रश्न (I)
6 Videos
- सरल रेखा में गति BOOK - HC VERMA HINDICHAPTER - सरल रेखा में गति EXERCISE - अभ्यास के प्रश्न
27 Videos
- सरल आवर्त गति पर आधारित अन्य गतियाँ BOOK - HC VERMA HINDICHAPTER - सरल आवर्त गति पर आधारित अन्य गतियाँ EXERCISE - अभ्यास के प्रश्न
8 Videos
- स्थितिज ऊर्जा एंव ऊर्जा - सरंक्षण का सिध्दांत BOOK - HC VERMA HINDICHAPTER - स्थितिज ऊर्जा एंव ऊर्जा - सरंक्षण का सिध्दांत EXERCISE - अभ्यास के प्रश्न
43 Videos
Similar Questions
यदि कोई कण एकसमान वेग से चल रहा हो,तो उसका औसत वेग , वेग तथा चाल सभी बराबर होंगे | इस कथन पर टिप्पणी करे |
View Solutionचित्र में x - अक्ष पर चलते एक कण का विस्थापन - समय ग्राफ दिखाया गया है | इस ग्राफ से पता चलता है कि
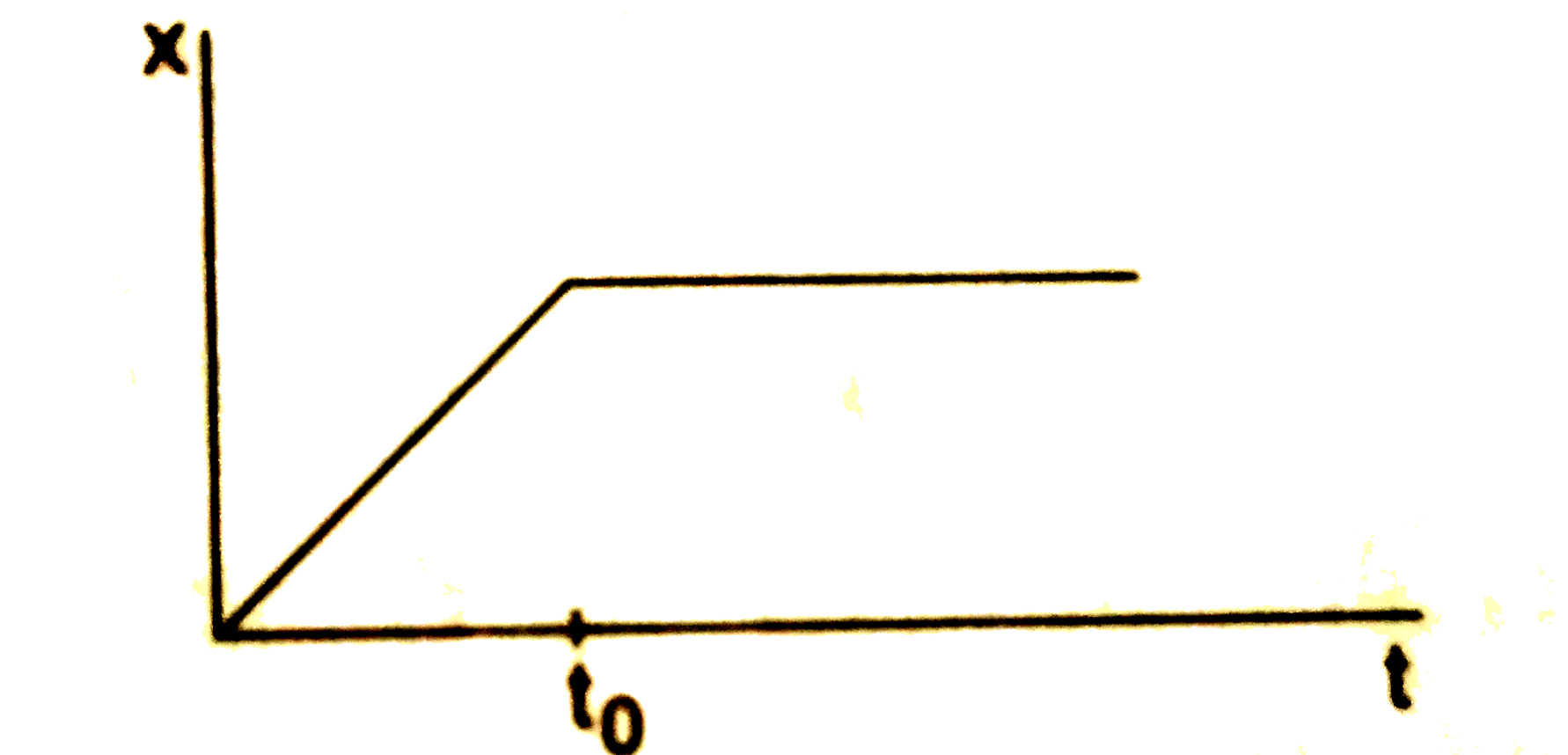
View Solutionएक कण मूलबिंदु से प्रारम्भ कर x - अक्ष पर चलता हुआ x = 20 m पर पँहुचता है और फिर उसी रेखा पर वापस मुड़कर x = -20 m पर आ जाता है | इस पूरी अवधि में कण द्वारा तय की गई दुरी तथा उसका विस्थापन बताएँ |
View Solutionएक कण को एकसाथ दो आवर्त गतियाँ प्रदान की जाती है जिसकी दिशाएँ समान है तथा आवर्तकाल भी सामान हैं। एक का आयाम 3.0 cm तथा दूसरे का आयाम 4.0 cm है। परिणामी गति का आवर्तकाल निकालें यदि दोनों के बीच का कलांतर (a)0∘(b)60∘ तथा (c)90∘ हो।
View Solutionएक संयंत्र में 50 m ऊँचाई से गिरनेवाले जल का उपयोग विद्युत - ऊर्जा उत्पादन के लिए किया जाता हैं । यदि प्रतिघंटा 1.8×105 kg जल गिरता है तथा इसकी गुरुत्वीय स्थितिज ऊर्जा का आधा भाग विद्युत ऊर्जा में परिवर्तित किया जा सकता हैं , तो इससे 100 W के कितने बल्ब जलाए जा सकते हैं ?
View Solutionदरअसल शुरू से ही था हमारे आदेशों में कही एक जानी दुश्मन कि घर को बचाना है लूटेरों से शहर को बचाना है नदियों से देश को बचाना है , देश के दुश्मनों से बचाना है - नदियों को नाला हो जाने से हवा को धुआँ हो जाने से खाने को जहर हो जाने से : बचाना है - जंगल को मरुस्थल हो जाने से , बचाना है - मनुष्य को , जंगल हो जाने से । शब्द - सारिणी की सहायता से समान अर्थ के शब्द ढूढ़कर लीखिए :
View Solutionबिंदु (3,4,0) की XY तल से लामिबक दुरी ज्ञात कीजिये
View Solutionएक रेखा X- अक्ष तथा Y-अक्ष को बिंदु A तथा B पर मिलती है AB का मध्य बिंदु (x1,y1) है तो रेखा का समीकरण है -
View Solutionबिंदु (18, 5, 12) की X-अक्ष से पर लंबवत्त दुरी........ है |
View Solutionनिम्नलिखित स्थितियों में एक चर बिंदु का बिन्दुपथ ज्ञात कीजिए जिसकी
y- अक्ष से दूरी , उसकी मूलबिंदु से दूरी की आधी है ।
View Solutionउस बिंदु का बिन्दुपथ ज्ञात कीजिए
जिसकी x-अक्ष से दूरी उसकी y-अक्ष से दूरी की तीन गुनी है ।
View Solutionएक बिंदु इस प्रकार गमन करता है कि उसकी बिंदु (3,4) से दुरी बिंदु (−3,−4) से उसकी दूरी की तिगुनी रहती है । उसका बिन्दुपथ ज्ञात कीजिए ।
View Solutionउस बिंदु का बिन्दुपथ जिसकी y-अक्ष से दूरी , उसकी मूलबिंदु से दूरी की आधी है ………… होगा ।
View Solutionएक 13 मीटर लम्बी सीढ़ी दीवार के सहारे झुकी हुई है। सीढ़ी के पाद को 1.5 मी./से. की दर से जमीन के सारे दीवार से दूर खींचा जाता है। सीढ़ी तथा जमीन के मध्य का कोण किस गति से परिवर्तित हो रहा है जबकि सीढ़ का पावि दीवार से 12 मीटर दूर हो ।
View Solutionवह समतल, जो बिन्दुओ (−3,−3,4) तथा (3,7,6) को मिलाने वाले रेखाखण्ड का लंबसमद्विभाजक करता है, निम्न में से किस एक बिंदु से होकर जाता है?
View Solutionएक वृत्त X-अक्ष पर एक जीवा काटता है जिसकी लम्बाई 4a है तथा यह वृत्त Y-अक्ष के एक बिन्दु से होकर जाता है जिसकी मूलबिंदु से दुरी 2b है , तो वृत्त के केन्द्र का बिन्दुपथ (locus) है
View Solution
