Consider the following parallel reactions being given by , each path being first order.
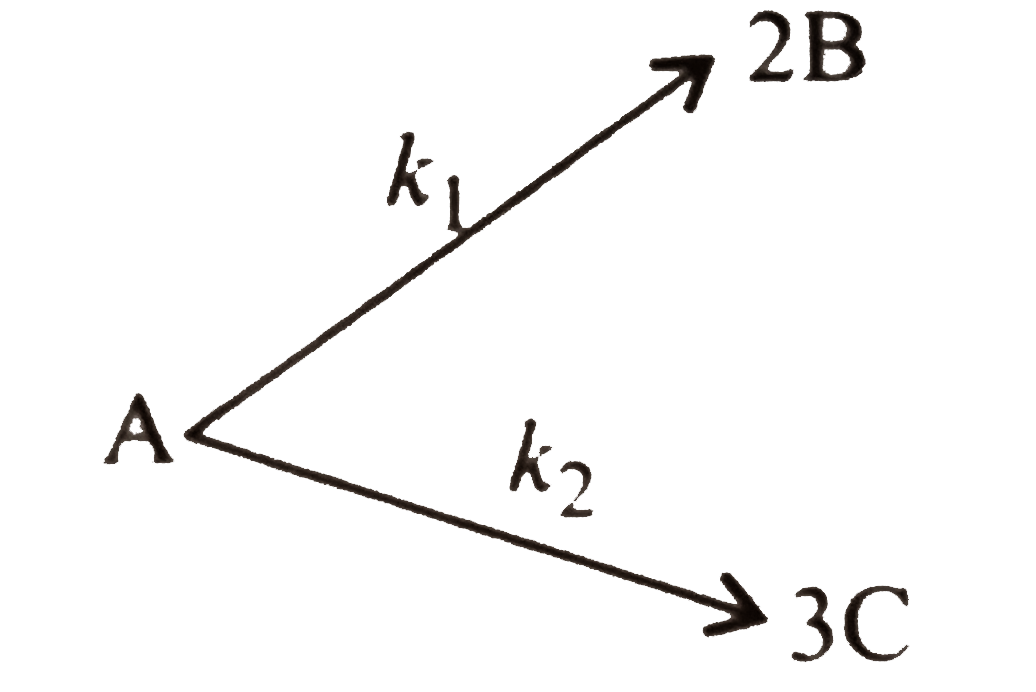
If the distribution of in the Product mixture is , the partical half life of for converison into is
The correct Answer is:A
and
Solving and and
Topper's Solved these Questions
- CHEMICAL KINETICSBook:CENGAGE CHEMISTRYChapter:CHEMICAL KINETICSExercise:Ex 4.3 More Than One Correct
Explore 5 Videos
- CHEMICAL KINETICSBook:CENGAGE CHEMISTRYChapter:CHEMICAL KINETICSExercise:Ex4.4 Objective
Explore 10 Videos
- CHEMICAL KINETICSBook:CENGAGE CHEMISTRYChapter:CHEMICAL KINETICSExercise:Ex 4.2 (Objective)
Explore 10 Videos
- CARBOXYLIC ACIDS AND THEIR DERIVATIVESBook:CENGAGE CHEMISTRYChapter:CARBOXYLIC ACIDS AND THEIR DERIVATIVESExercise:Exercises Archives (Analytical And Descriptive)
Explore 34 Videos
- COORDINATION COMPOUNDSBook:CENGAGE CHEMISTRYChapter:COORDINATION COMPOUNDSExercise:Archives Subjective
Explore 18 Videos
Similar Questions
Consider the following parallel first order reactions:
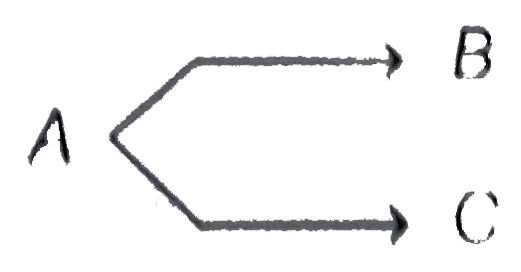
Half-life of the overall decay of A is 2 ys while half-life for the formation of B is 3yr. Half-life for the formation for C (in years) is :
View SolutionA first order gas reaction has k=1.5×10−6s−1 at 200∘C. If the reaction is allowed to run for 10h, what have changed in the Product? What is the half-life of this reaction?
View Solution
Knowledge Check
Half life (t12) of first order reaction is
Adependent of concentrationBindependent of concentrationCdependent of timeDdependent of molecularityThe half life of a first order reaction having rate constant k=1.7×10−5sec−1 is :
A12.1 hB9.7 hC11.3 hD1.8 hHalf life (t1) of the first order reaction and half life (t2) of the 2nd order reaction are equal. If initial concentration of reactants in both reaction are same then ratio of the initial rate of the reaction
A1B2C0.693D1.44
Show that in the first order reaction, time required for completion of 99.9% is 10 times that of half-life (t1/2) of the reaction.
View SolutionFor the following elementary first order reaction:
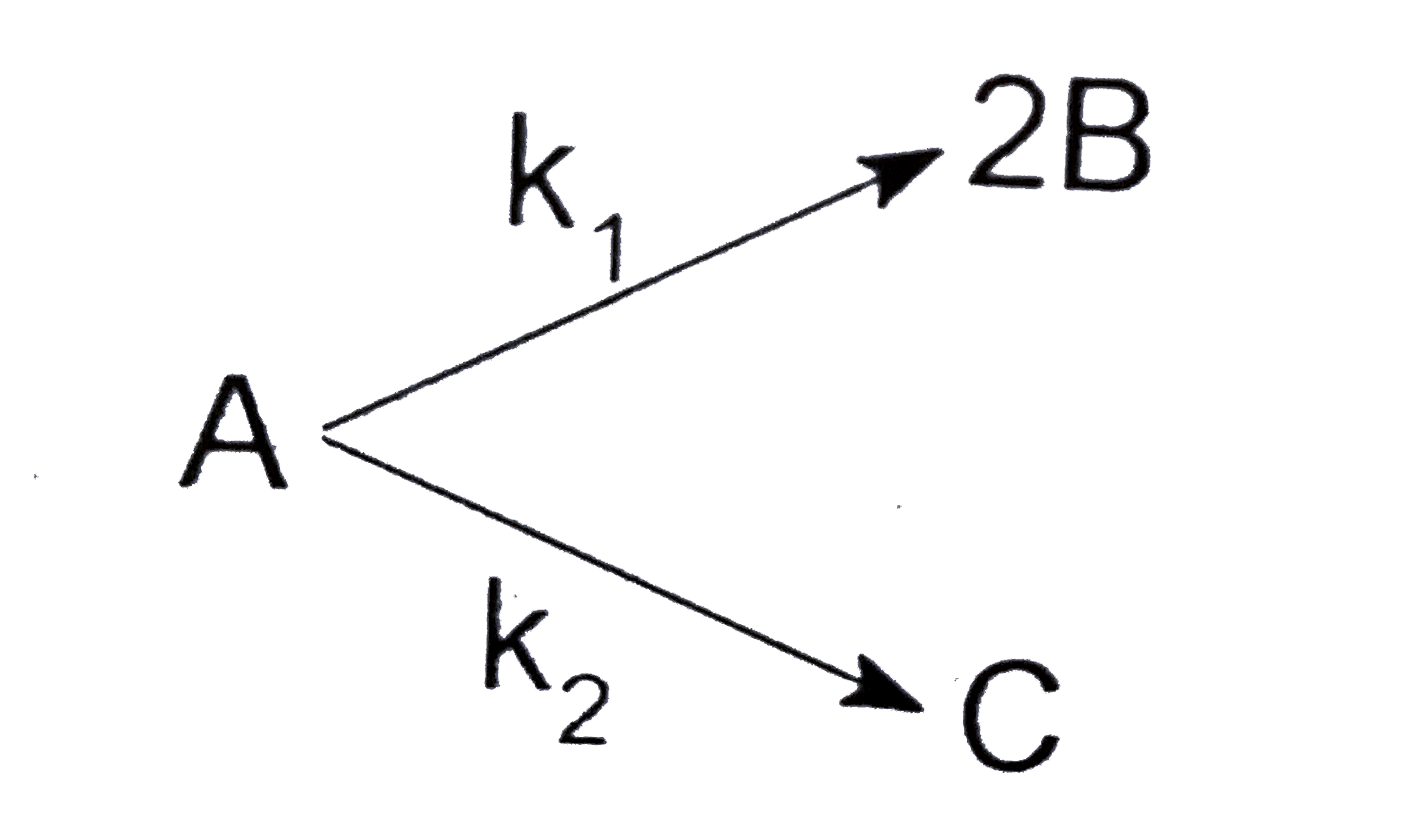
If k2=2k1, then % of B in overall product is:
View SolutionThe rate constant of a first-order reaction of the type 2A→P is 1.5×10−1s−1. The half-life period of the reaction is
View SolutionHalf-life (t1) of the first order reaction and half-life (t2) of the second order reaction are equal. Hence ratio of the rate at the start of the start of the reaction:
View SolutionConsider following two competing first ordr reactions,
Pk1−−→A+B,Qk2−−→C+D
if 50% of the reaction oof P wascompleted when 96% of Q was complete ,then the ratio (k2/k1) will be :
View Solution

