Given that $Δ T_{f}$ is the depression in freezing point of the solvent in a solution of a non-volatile solute of molarity $m$ ,the quantity $L t m \to 0 (Δ T_{f} / m)$ is equal to ……………. .

Video Solution

Text Solution

Generated By DoubtnutGPT

To solve the problem, we need to analyze the relationship between the depression in freezing point (ΔTf), molarity (m), and the freezing point depression constant (Kf) for a non-volatile solute.
1. Understand the Formula for Depression in Freezing Point:
The depression in freezing point (ΔTf) is given by the formula:
$Δ T_{f} = K_{f} \cdot m \cdot i$
where:
- $K_{f}$ is the freezing point depression constant,
- $m$ is the molarity of the solution,
- $i$ is the van 't Hoff factor (which is 1 for non-volatile solutes).
2. Consider the Limit as Molarity Approaches Zero:
We are interested in the quantity:
$lim m \to 0 (\frac{Δ T_{f}}{m})$
As the molarity $m$ approaches zero, we need to analyze what happens to $Δ T_{f}$ .
3. Substituting the Formula into the Limit:
Substitute the expression for ΔTf from the first step into the limit:
$\frac{Δ T_{f}}{m} = \frac{K_{f} \cdot m \cdot i}{m}$
Here, since $i = 1$ for a non-volatile solute, we can simplify this to:
$\frac{Δ T_{f}}{m} = K_{f} \cdot i = K_{f} \cdot 1 = K_{f}$
4. Taking the Limit:
Now, as $m$ approaches 0, the expression simplifies to:
$lim m \to 0 (\frac{Δ T_{f}}{m}) = K_{f}$
5. Conclusion:
Therefore, the quantity $lim m \to 0 (\frac{Δ T_{f}}{m})$ is equal to $K_{f}$ .
Final Answer:
$lim m \to 0 (\frac{Δ T_{f}}{m}) = K_{f}$
---

Updated on:7/8/2024

Given that $Δ T_{f}$ is the depression in freezing point of the solvent in a solution of a non-volatile solute of molarity $m$ ,the quantity $L t m \to 0 (Δ T_{f} / m)$ is equal to ……………. .
AZero
BOne
CThree
DNone of the above
Consider following figure and answer the questions at the end of it.
Figure explains elevation in boiling point when a non-volatile solute is added to a solvent.

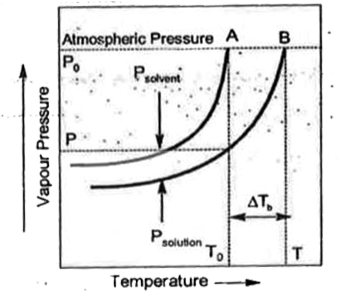
Variation of vapour pressure with temperature and showing elevation in boiling point.
Given that $Δ T_{b}$ is the elevation in boiling point of the solvent in a solution of molality 'm' then $L t m \to 0 (\frac{D η l T_{b}}{m})$ is equal to
A $K_{b}$ (molal elevation constant)
B $L_{v}$ (latent heat of vaporization)
C $Δ S$ (entropy change)
Dx (mole fraction of solute)
Consider following figure and answer the questions at the end of it. Figure explains elevation in boiling point when a non-volatile solute is added to a solvent.

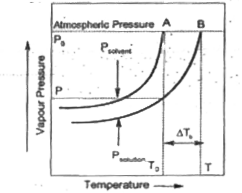
Variation of vapour pressure with temperature and showing elevation in boiling point.
Given that $Δ T_{b}$ is the elevation in boiling point of the solvent in a solution of molality m then $L t m \to 0 (\frac{Δ T_{b}}{m})$ is equal to
A $K_{b}$ (molal elevation constant)
B $L_{y}$ (latent heat of vaporization)
C $Δ S$ (entropy change)
Dx (mole fraction of solute)