A crystal is made up of particals X, Y, and Z. X froms f packing. Y occupies all octahedral voids of X and Z occupies all tetrahedral voids of X. If all the particles along one body diagonal are removed. Then the fromula of the crystal would be
XYZ2
X2YZ2
X8Y4Z5
X5Y4Z8
The correct Answer is:D
For fcc, number of X atoms =4/unit cell
Number of TVs=8Z
Number of OVs=4Y
Number of atoms removed along one body diagonal =2X(corner) and 2Z(TVs) are 1Y (OV at body centre)
∴ Number of X atoms left =4−(2×18)=154
Number of Y atoms left =4−(1×1)=3
Number of Z atoms left =8−(2×1)=6
The simplest formula =X154Y3Z6⇒X15Y12Z24
⇒X5Y4Z8
Topper's Solved these Questions
- SOLID STATEBook:CENGAGE CHEMISTRYChapter:SOLID STATEExercise:Exercises (Assertion-Reasoning)
Explore 19 Videos
- SOLID STATEBook:CENGAGE CHEMISTRYChapter:SOLID STATEExercise:Exercises (Interger)
Explore 9 Videos
- SOLID STATEBook:CENGAGE CHEMISTRYChapter:SOLID STATEExercise:Exercises (Multiple Correct)
Explore 39 Videos
- REDUCTION AND OXIDATION REACTION OF ORGANIC COMPOUNDSBook:CENGAGE CHEMISTRYChapter:REDUCTION AND OXIDATION REACTION OF ORGANIC COMPOUNDSExercise:SUBJECTIVE TYPE
Explore 3 Videos
- SOLUTIONSBook:CENGAGE CHEMISTRYChapter:SOLUTIONSExercise:Ex 2.3 (Objective)
Explore 9 Videos
Similar Questions
A crystal is made of particles X,Y and Z.X form fcc packing . Y occupies all the octahedral void of X and Z occupies all the tetrahedral voids of X . If all the particles along one body diagonal are removed then the formula of the crystal would be:
View SolutionIn a crystalline solid, atom of A form fcc packing and atoms of B occupy all octahedral voids. If all the atoms along one body diagonal are removed then what will be the simplest formula of the crystalline solid ?
View Solution
Knowledge Check
A crystal is made of particle X,Y and Z 'X' forms +FCC packing+. 'Y' occupies all the octahedral voids of X and Z occupies all tetrahedral voiods of X. If all the particles along one body diagonal are removed, then the formula of the crystal would be?
AXYZ2BX2YZ2CX8Y4Z5Dnone of theseA crystal is made up of particles A. B and C. A forms fcc packing, B occupies all octahedral voids and C occupies all tetrahedral voids. If all the particles along one body diagonal are removed, then the formula of the crystal would be
AABC2BA2BC2CA8B4C5DA5B4C8A crystal is made of particles X and Y.X form fcc packing and Y occupies all the octahedral voids . If all the particles along one body diagonal are removed then the formula of the crystal would de :
AX4Y3BX5Y5CX4Y5DNone of these
A forms ccp lattice B occupy half of the octahedral voids and O occupy all the tetrahedral voids. Calculate formula-
View SolutionA crystal is made of particles A and B . From fcc packing and B occupies all the octahedral voids . If all the particle along the plane as shown in figure are removed , then, the formula of the crystal would be :
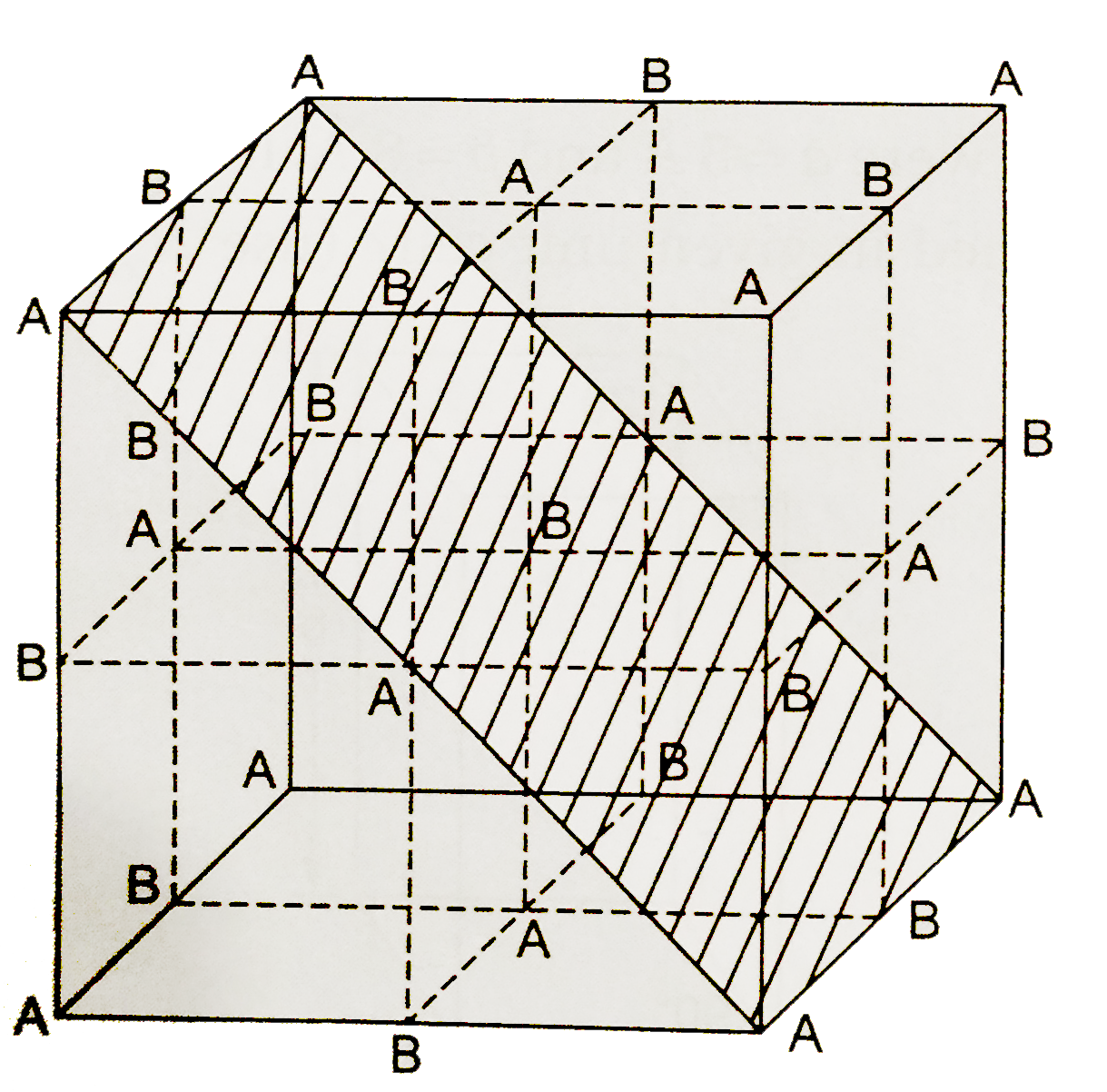
View SolutionA crystal is made of particles A and B. A forms FCC packing and B occupies all the octahedral voids. If all the particles along the plane as shown in figure are removed, then the formula of the crystal would be :
View SolutionA crystal is made of particles X and Y. X forms FCC packing and Y occupies all the octahedral voids. Find the formula of the crystal if all the particles along one body diagonal are removed.
View SolutionIn a crystalline solid,atoms of X from fcc packing and the atoms of Y occupy all octahedral voids.If the atoms along one body diagnal are removed then the simplest formula of the crystalline solid will be:
View Solution

