The value of $K_{c}$ for the reaction:
$A_{2} (g) + B_{2} (g) \Leftrightarrow 2 A B (g)$
at $100^{\circ} C$ is $49$ . If $1.0 L$ flask containing one mole of $A_{2}$ is connected with a $2.0 L$ flask containing one mole of $B_{2}$ , how many moles of AB will be formed at $100^{\circ} C$ ?

Video Solution

Text Solution

Verified by Experts

$A_{2} (g) + B_{2} (g) \Leftrightarrow 2 A B (g)$
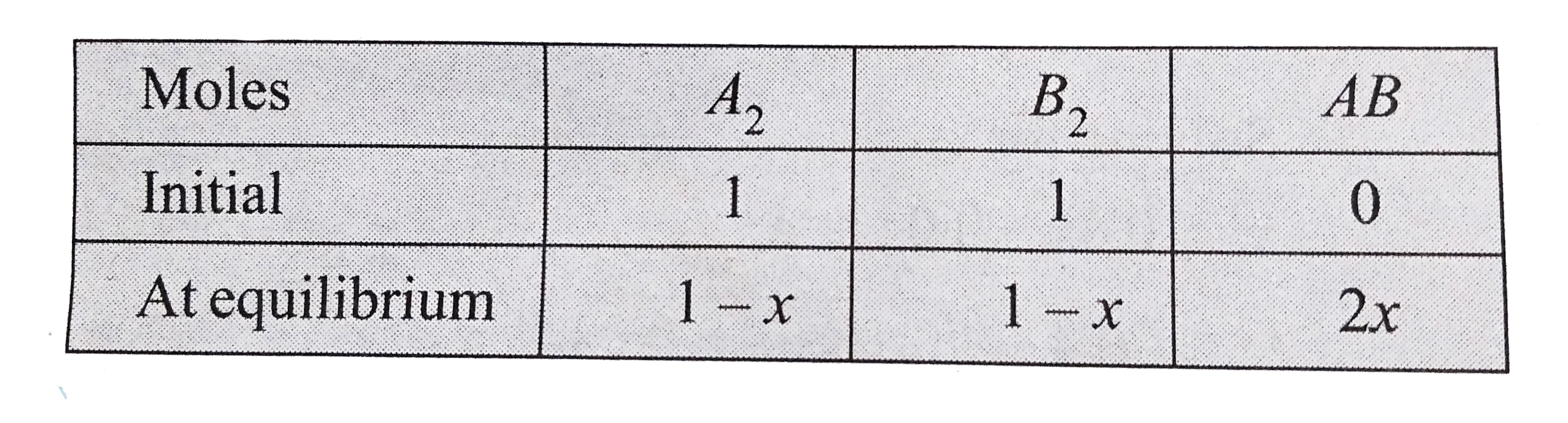
As the two vessels are connected, the final volume is now $3.0 L$ . Let $x$ mol each of $A_{2}$ and $B_{2}$ react to form $2 x$ moles of $A B_{2}$ (from stoichiometry of reaction).

$K_{c} = \frac{{[A B]}^{2}}{[A_{2}] [B_{2}]} = 49$
Concentration species at equilibrium are
$[A_{2}] = (1 - x) / 3, [B_{2}] = (1 - x) / 3, [A B] = 2 x / 3$
$K_{c} = \frac{{(\frac{2 x}{3})}^{2}}{(\frac{1 - x}{3}) (\frac{1 - x}{3})} = \frac{4 x^{2}}{{(1 - x)}^{2}} = 49$
Taking square root on both sides:
$\Rightarrow \frac{2 x}{1 - x} = 7 \Rightarrow x = 0.78$
rArr "moles" of $A B (g)$ formed at equilibrium $= 2 x = 1.56$

Updated on:21/07/2023

The equilibrium constant of the reaction $A_{2} (g) + B_{2} (g) \Leftrightarrow 2 A B (g)$ at 373 K is 50. If 1 L of flask containing 1 mole of $A_{2}$ (g) is connected to 2 L flask containing 2 moles $B_{2}$ (g) at $100^{\circ} C$ , the amount of AB produced at equilibrium at $100^{\circ} C$ would be
A0.93 mol
B1.87 mol
C2.80 mol
D3.74 mol
The equilibrium constant of the reaction $A_{2} (g) + B_{2} (g) \Leftrightarrow 2 A B (g)$ at 373 K is 50. If 1 L of flask containing 1 mole of $A_{2}$ (g) is connected to 2 L flask containing 2 moles $B_{2}$ (g) at $100^{\circ} C$ , the amount of AB produced at equilibrium at $100^{\circ} C$ would be
A0.93 mol
B1.87 mol
C2.80 mol
D3.74 mol
The equilibrium constant of the reaction $A_{2} (g) + B_{2} (g) \Leftrightarrow 2 A B (g)$ at 373 K is 50. If 1 L of flask containing 1 mole of $A_{2} (g)$ is connected to 2L flask containing 2 moles $B_{2} (g)$ at $100^{\circ} C$ , the amount of AB produced at equilibrium at $100^{\circ} C$ would be
A0.93 mol
B1.87 mol
C2.80 mol
D3.74 mol