The equation α=D−d(n−1)d is correctly matched for: (α is the degree of dissociation, D and d are the vapour densities before and after dissociation, respectively).
The correct Answer is:B
To solve the problem, we need to analyze the equation given and determine which reaction corresponds to it based on the degree of dissociation (α), the vapor densities (D and d), and the number of moles of products (n).
1. Understand the Variables:
- α (degree of dissociation): This represents the fraction of the original substance that has dissociated into products.
- D (vapor density before dissociation): This is the vapor density of the original substance before any dissociation occurs.
- d (vapor density after dissociation): This is the vapor density of the system after some of the original substance has dissociated.
- n (number of moles of products): This is the total number of moles of products formed after dissociation.
2. Analyze the Equation:
- The equation given is:
α=D−d(n−1)d
- Here, the term D−d represents the change in vapor density due to dissociation, and (n−1)d represents the effective change in moles as a result of the dissociation.
3. Identify the Reaction:
- We need to find a reaction where the number of moles of products (n) can be expressed correctly in relation to the degree of dissociation.
- The options provided in the question will likely represent different dissociation reactions.
4. Evaluate Each Option:
- For each option, calculate the total number of moles of products formed after dissociation and check if it equals n.
- For example:
- If a reaction produces n2+n3 moles, simplify it to see if it equals n.
- Continue this for each provided option.
5. Determine the Correct Option:
- After evaluating the options, we find that the only reaction that satisfies the condition n=total moles of products is option B.
Final Answer:
The correct option that matches the equation α=D−d(n−1)d is Option B.
- α (degree of dissociation): This represents the fraction of the original substance that has dissociated into products.
- D (vapor density before dissociation): This is the vapor density of the original substance before any dissociation occurs.
- d (vapor density after dissociation): This is the vapor density of the system after some of the original substance has dissociated.
- n (number of moles of products): This is the total number of moles of products formed after dissociation.
- The equation given is:
α=D−d(n−1)d
- Here, the term D−d represents the change in vapor density due to dissociation, and (n−1)d represents the effective change in moles as a result of the dissociation.
- We need to find a reaction where the number of moles of products (n) can be expressed correctly in relation to the degree of dissociation.
- The options provided in the question will likely represent different dissociation reactions.
- For each option, calculate the total number of moles of products formed after dissociation and check if it equals n.
- For example:
- If a reaction produces n2+n3 moles, simplify it to see if it equals n.
- Continue this for each provided option.
- After evaluating the options, we find that the only reaction that satisfies the condition n=total moles of products is option B.
The correct option that matches the equation α=D−d(n−1)d is Option B.
Topper's Solved these Questions
- BOOK - CENGAGE CHEMISTRYCHAPTER - CHEMICAL EQUILIBRIUMEXERCISE - Concept Applicationexercise 7.153videos
CHEMICAL EQUILIBRIUM
- BOOK - CENGAGE CHEMISTRYCHAPTER - CHEMICAL EQUILIBRIUMEXERCISE - Ex 7.240videos
CHEMICAL EQUILIBRIUM
- BOOK - CENGAGE CHEMISTRYCHAPTER - CHEMICAL BONDING AND MOLECULAR STRUCTUREEXERCISE - Archives Subjective15videos
CHEMICAL BONDING AND MOLECULAR STRUCTURE
- BOOK - CENGAGE CHEMISTRYCHAPTER - CLASSIFICATION AND NOMENCLATURE OF ORGANIC COMPOUNDSEXERCISE - Analytical and Descriptive Type3videos
CLASSIFICATION AND NOMENCLATURE OF ORGANIC COMPOUNDS
Similar Questions
Derive the equation, α=i−1n−1
Derive a relation between degree of dissociation and van't Hoff factor.View SolutionPCl3 dissociates into PCl3 and Cl2 . If the total pressure of the system in equilibrium is p at a density, d, and temperature, T, show that
α=pMdRT−1
where α is the degree of dissociation, M is the relative molar mass of PCl3 . If the vapour density has the value 62 when the temperature is 230∘C, what is the value of p/d?View Solution
Knowledge Check
- Question 1 - Select One
Correct statement for α-D-glucose is
ACan show mutarotionBDo not give 2,4-DNP testCShow reducing property with Tollen's reagentDAll of these - Question 2 - Select One
In the dissociation of N2O4 into NO2.(1+x) values with the vapour densities ratio (Dd) is given by :
A
B
C
D
- Question 3 - Select One
In the dissociation of N2O4 into NO2O4 into NO2,α varies with (Dd) according to: [α degree of dissociation, D-vapour density before dissociation, d-vapour density after dissociation]
A
B
C
D
In the dissociation of N2O4 into NO2.(1+x) values with the vapour densities ratio (Dd) is given by :
View SolutionFor the reaction A(g)+B(g)⇔C(g)+D(g), the degree of dissociation α would be –
View SolutionPolymer of α-D glucose is
View SolutionFor the dissociation of PCl5 into PCl3 and Cl2 in gaseous phase reaction , if d is the observed vapour density and D the theoretical vapour density with 'α' as degree of dissociation ,variaton of D/d with 'α' is given by ?
View SolutionIn α-D-Glucose, the anomeric carbon is at:
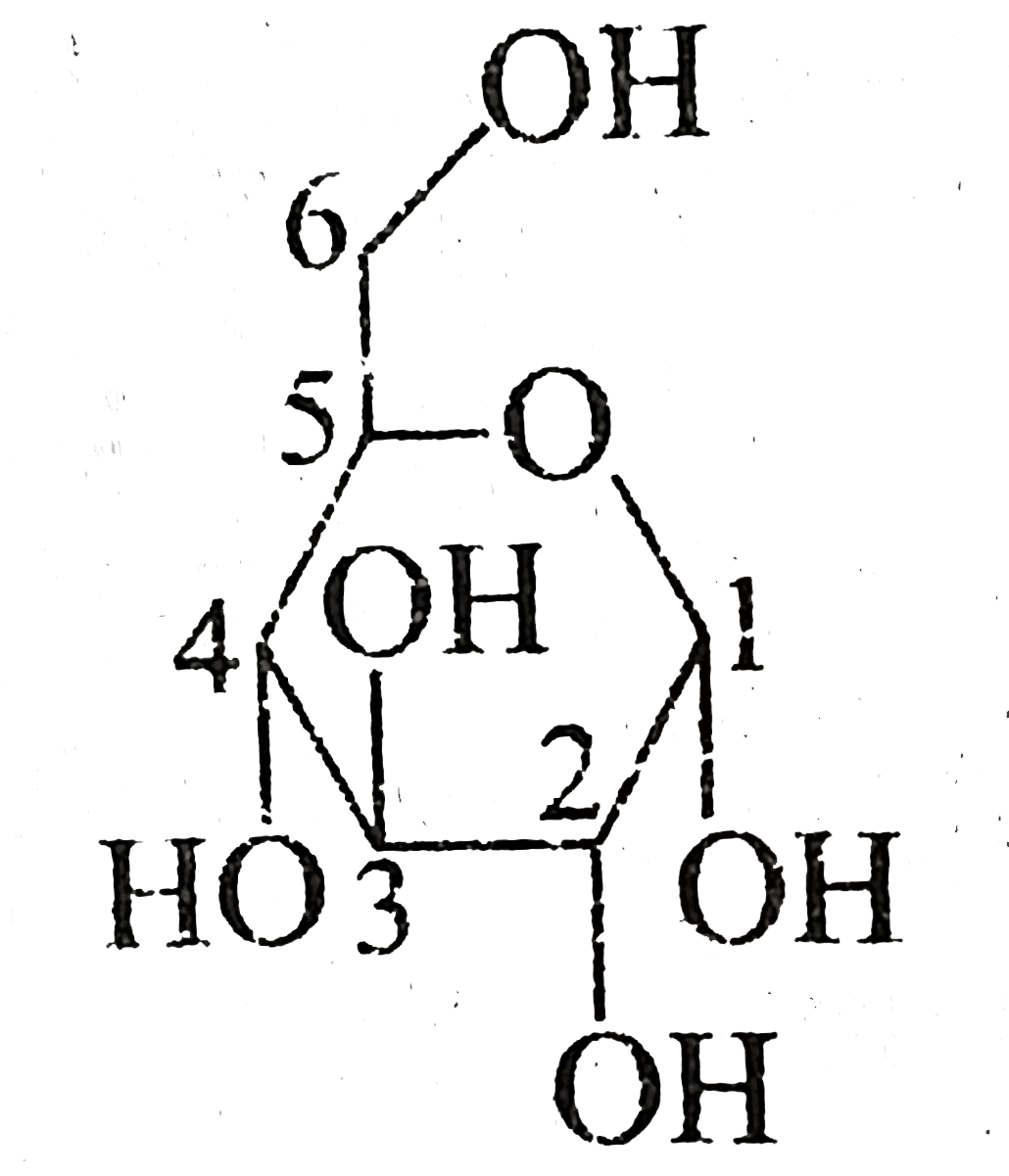View Solution