The direct conversion of A to B is difficult, hence it is carried out as
A→C→D→B
Given, ΔS(A→C)=50eU,ΔS(C→D)=30eU,ΔS(B→D)=20eU, where eU is entropy unit. Thus the change in entropy in (A→B) is:
100eU
60eU
−100eU
−60eU
To solve the problem of finding the change in entropy from A to B through the intermediate steps, we can follow these steps:
1. Identify the given entropy changes:
- ΔS(A→C)=50eU
- ΔS(C→D)=30eU
- ΔS(B→D)=20eU
2. Determine the entropy change from D to B:
- The change in entropy from D to B is the negative of the change from B to D:
ΔS(D→B)=−ΔS(B→D)=−20eU
3. Calculate the total change in entropy from A to B:
- The total change in entropy from A to B can be expressed as the sum of the individual changes:
ΔS(A→B)=ΔS(A→C)+ΔS(C→D)+ΔS(D→B)
- Substituting the values we have:
ΔS(A→B)=50eU+30eU−20eU
4. Perform the calculation:
ΔS(A→B)=50+30−20=60eU
5. Final Result:
- The change in entropy from A to B is:
ΔS(A→B)=60eU
- ΔS(A→C)=50eU
- ΔS(C→D)=30eU
- ΔS(B→D)=20eU
- The change in entropy from D to B is the negative of the change from B to D:
ΔS(D→B)=−ΔS(B→D)=−20eU
- The total change in entropy from A to B can be expressed as the sum of the individual changes:
ΔS(A→B)=ΔS(A→C)+ΔS(C→D)+ΔS(D→B)
- Substituting the values we have:
ΔS(A→B)=50eU+30eU−20eU
ΔS(A→B)=50+30−20=60eU
- The change in entropy from A to B is:
ΔS(A→B)=60eU
Topper's Solved these Questions
Similar Questions
The direct conversion of A or B is difficult, hence it is carried out by the following shown path
Given, ΔSA→C=50eu, ΔSC→D=30eu,ΔSB→D=20eu
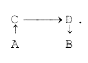
Where eu is entropy unit, then ΔSA→B is .
View SolutionThe conversion A to B is carried out by the following path : C→D↑ ↓A B Given : ΔS(A→C)=50 e.u. ,
ΔS(C→D)=30 e.u., ΔS(B→D)=20 e.u.
where e.u. is entropy unit then ΔS(A→B) is
View Solution
Knowledge Check
The direct conversion of A to B is difficult. Hence it is carried out by the following shown path:
ΔS(A→C)=50e.u.,ΔS(C→D)=30e.u,
ΔS(B→D)=20e.u where e.u is entropy unit.
Then ΔS(A→B),
A+100e.u.B+60 e.u.C−100e.u.D−60e.u.The direct conversion of A to B is difficult. Hence it is carried out by the following shown path:
ΔS(A→C)=50e.u.,ΔS(C→D)=30e.u,
ΔS(B→D)=20e.u where e.u is entropy unit.
Then ΔS(A→B),
A+100e.uB+60e.uC−100e.uD−60e.uThe direct conversion of A to B is difficult, hence, it is carried out by the following path:

Given:
ΔSA→C=50 c.u,
ΔSC→D=30 c.u.
ΔSB→D=20 c.u where e.u is the entropy unit.
Then, ΔSA→B is:A+60 euB+100 e.uC−60 e.uD100 e.u
A gaseous reactant A forms two different product, in parallel reaction , B and C as follows:
A→B,ΔH∘=−3KJ,ΔS∘=20JK−1 , A→C,ΔH∘=−3.6KJ,ΔS∘=10JK−1
Discuss the relative stability of B and C on the basis of Gibb's free energy change at 27∘C.
View SolutionThe conversion A to B is carried out by the following path : C→D↑ ↓A B Given : ΔS(A→C)=50 e.u. ,
ΔS(C→D)=30 e.u., ΔS(B→D)=20 e.u.
where w.u. is entropy unit then ΔS(A→B) is
View SolutionThe direct conversion of A to B is difficult, hence is carried out by the following shown path:
Δ(A→C)=50,ΔS(C→D)=30,ΔS(B→D)=20 The entropy change for the process A→B is :
View Solutiona process A→D is difficult to occur directly instead it takes place in three successive steps, ΔS(A→B)=40 e.u., ΔS(B→C)=30 e.u., ΔS(D→C)=20 e.u. where e.u. is entropy unit then the entropy change ΔS for the process (A→D) is
View SolutionA process A→B is difficult to occur directly instead it takes place in the three successive steps.
ΔS(A→C)=50e.u.
ΔS(C→D)=30e.u.
ΔS(B→D)=20e.u. where e.u. is entropy unit. Then the entropy change for the process ΔS(A→B) is:
View Solution
