A gas is expanded from volume V1 to V2 through three different process:
a. Reversible adiabatic
b. Reversible isothermal
c. Irreversible adiabatic (against a constant external pressure Pex)
The correct option is
[(Tf)Gas]Reversible isothermal>[(Tf)GaS]Reversible adiabatic>[(Tf)Gas]Irreversible adiabatic
[(Tf)Gas]Reversible isothermal>[(Tf)GaS]Irreversible adiabatic>[(Tf)Gas]Reversible adiabatic
wReversible isothermal >wIrreversible adiabatic>wReversible adiabatic
(Pf)Reversible isothermal>(Pf)Reversible adiabatic>(Pf)Irreversible adiabatic
wIsothermal>wAdiabatic and wRev.>WIrr.
(Rev.)(II)(Rev.)(I)
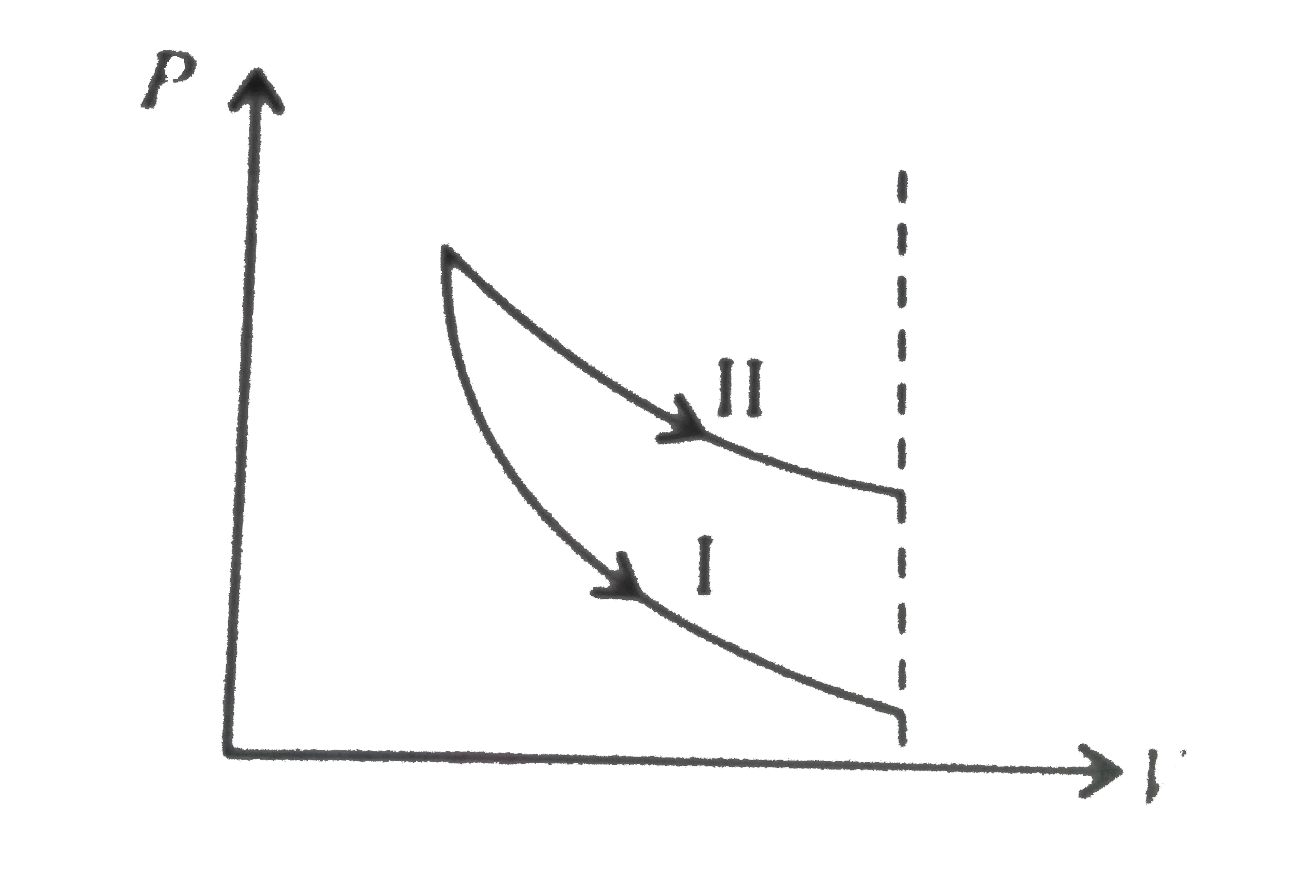
⇒WRev.isothermal>WRev.adiabatic>Wirr.adiabatic
In adiabatic expansion, T↓. More is the work done by the gas, more is the decrease in T.
(∵ Work is being done at the expense of ΔU)
Topper's Solved these Questions
Similar Questions
The ratio of slopes of P−V plots for reversible adiabatic process and reversible isothermal process of an ideal gas is equal to :
View SolutionA gaseous sample is generally allowed to do only expansion/compression type of work against its surroundings. The work done in case of an irreversible expansion ( in the intermediate stages of expansion/ compression the states of gases are not defined). The work done can be calculated using
dw=−PextdV
while in case of reversible process the work done can be calculated using
dw=-PdV where P is pressure of gas at some intermediate stages. Like for an isothermal reversible process, since
P=nRTV,so,
w=∫dw=−∫VfVinRTV.dV=−nRT In(VfVi)
Since,dw=PdV, so magnitude of work done can also be calculated by calculating the area under the PV curve of the reversible process in PV diagram.
If four identical samples of an ideal gas initially at similar state (P0,V0,T0) are allowed to expand to double their volumes by four different processes.

(P)By isothermal irreversible process
(Q) By reversible process having equation P2V= constant
(R) By reversible adiabatic process
(S)By irreversible adiabatic expansion against constant external pressure. Then in the graph shown the final state is represented by four different points then, the correct match can be :
View Solution
Knowledge Check
A sample of gas is compressed from an initial volume of 2V0toV0 using three different processes.
First: Using reversing isothermal
Second : Using reversible adiabatic
Third : Using irreversible adiabatic under a constant external pressure ,than :AFinal temerature of gas will be highest at the end of third process.BFinal temperature of gas will be highest at the end of second processCEnthalpy change of sample will be highest in isothermal process. (magnitude wise)DFinal pressure of gas will be highest at the end of second process.A gas is expanded form volume V0→2V0 under three different processes as shown in the figure . Process 1 is isobaric process process 2 is isothermal and and process 3 is adiabatic .
Let ΔU1,ΔU2andΔU3 be the change in internal energy of the gs in these three processes then
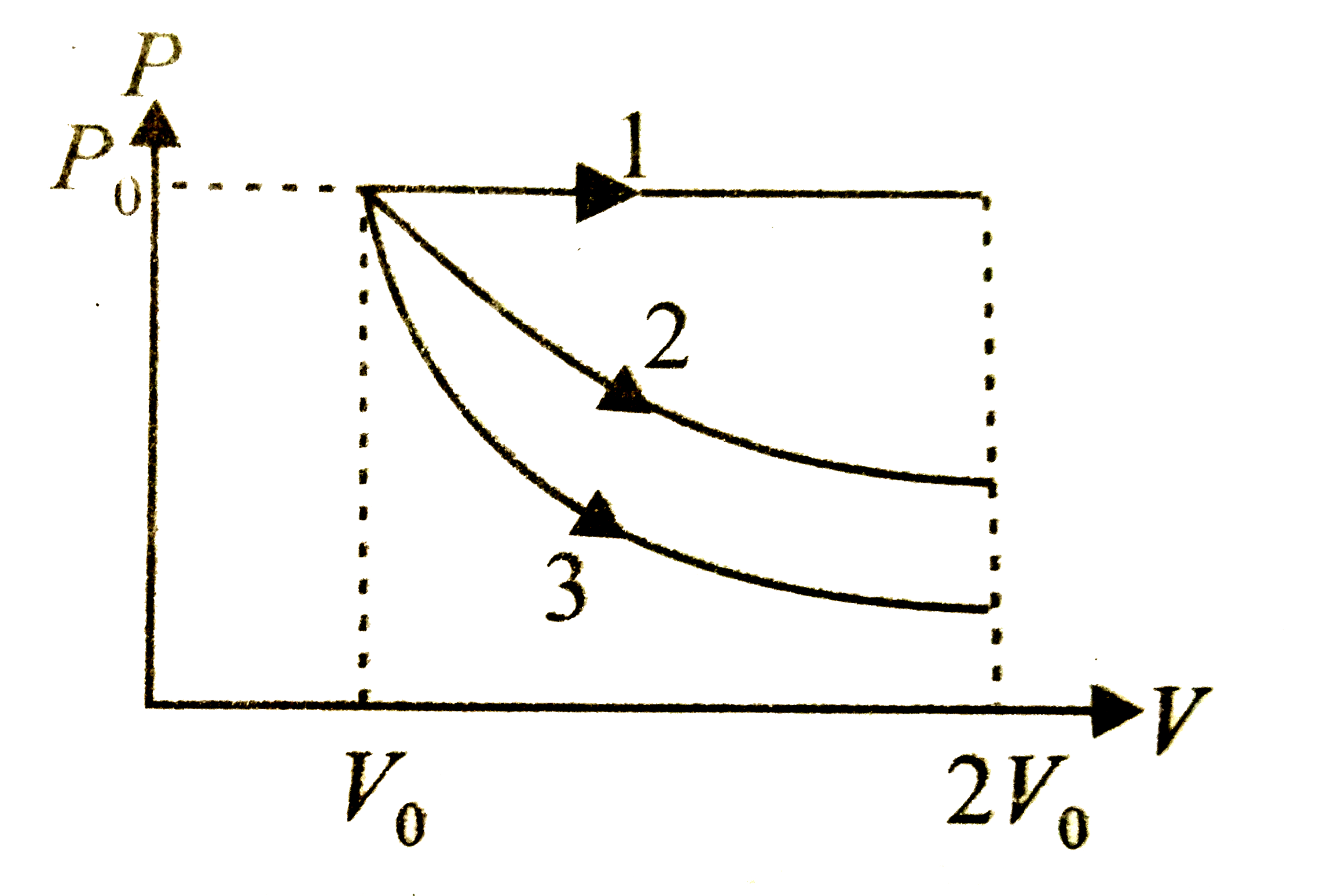 A△U1>△U2>△U3B△U1<△U3<△U2C△U2<△U3<△U3D△U2<△U3<△U1
A△U1>△U2>△U3B△U1<△U3<△U2C△U2<△U3<△U3D△U2<△U3<△U1A gas is expanded from volume V0 to 2V0 under three different processes, as shown in the figure. Process 1 is isobaric process, process 2 is isothermal and process 3 is adiabatic. Let ΔU1,ΔU2 and ΔU3 be the change in internal energy of the gas in these three processes. Then
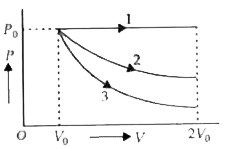 AΔU1>ΔU2>ΔU3BΔU1<ΔU2<ΔU3CΔU2<ΔU1<ΔU3DΔU2<ΔU3<ΔU1
AΔU1>ΔU2>ΔU3BΔU1<ΔU2<ΔU3CΔU2<ΔU1<ΔU3DΔU2<ΔU3<ΔU1
A gaseous sample is generally allowed to do only expansion/compression type work against its surroundings The work done in case of an irreversible expansion ( in the intermediate stages of expansion/compression the states of gases are not defined). The work done can be calculated using
dw=−PextdV
while in case of reversible process the work done can be calculated using
dw=−PdV where P is pressure of gas at some intermediate stages. Like for an isothermal reversible process. Since P=nRTV, so
w=∫dW=−vf∫vinRTV.dV=−nRTln(VfVi)
Since dw=PdV so magnitude of work done can also be calculated by calculating the area under the PV curve of the reversible process in PV diagram.
If four identical samples of an ideal gas initially at similar state (P0,V0,T0) are allowed to expand to double their volumes by four different process.
I: by isothermal irreversible process
II: by reversible process having equation P2V= constant
III. by reversible adiabatic process
IV. by irreversible adiabatic expansion against constant external pressure.
Then, in the graph shown in the final state is represented by four different points then, the correct match can be
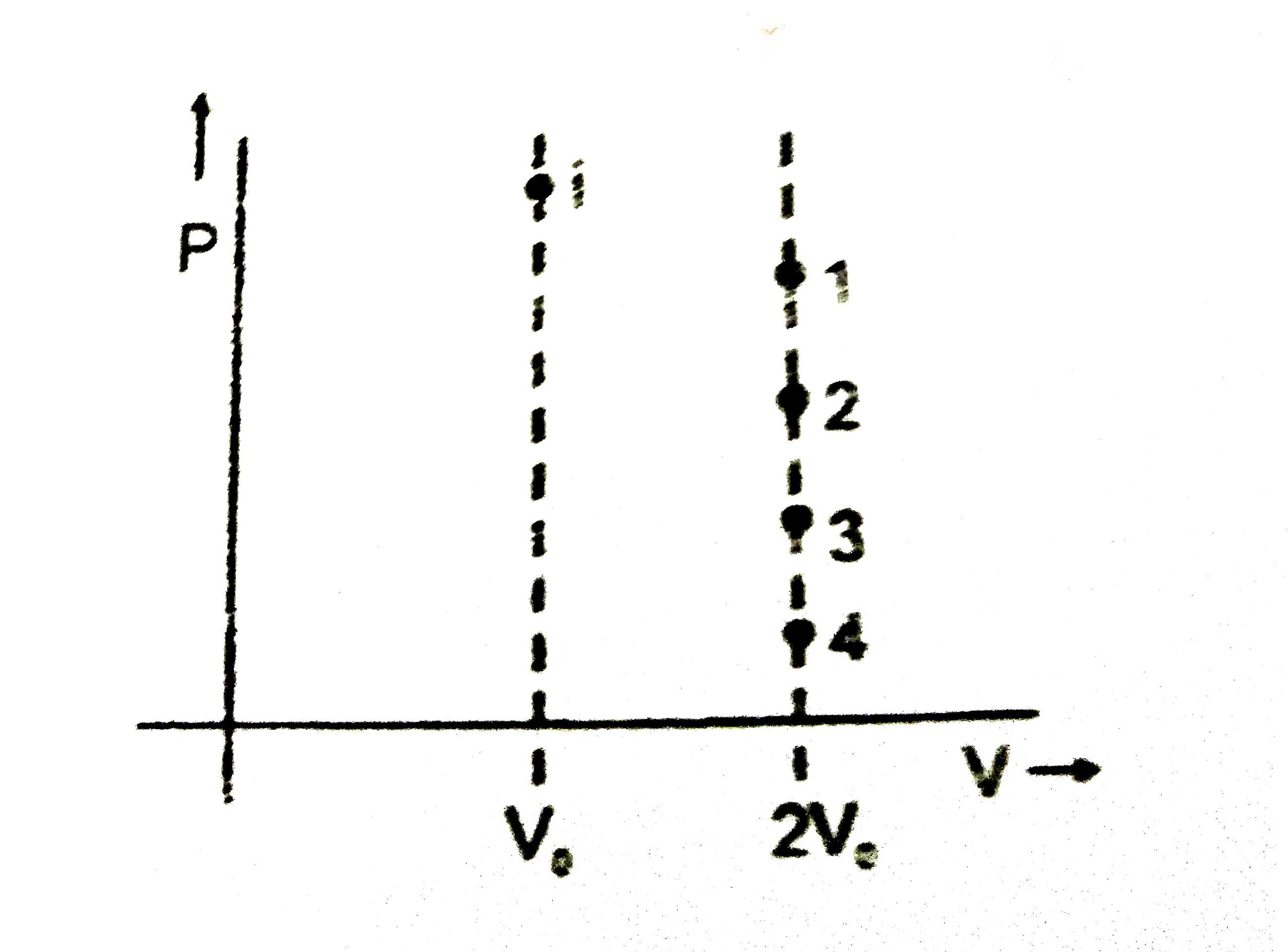
View SolutionA gas is expanded form volume V0→2V0 under three different processes as shown in the figure . Process 1 is isobaric process process 2 is isothermal and and process 3 is adiabatic .
Let ΔU1,ΔU2andΔU3 be the change in internal energy of the gs in these three processes then

View SolutionA gas expands under constant pressure P from volume V1 toV2The work done by the gas is
View SolutionSelect the correct statement for an ideal gas undergoinf reversible or irreversible adiabatic process from same initial process
View SolutionAn ideal gas expands isothermally from volume V1 to V2 and is then compressed to original volume V1 adiabatically. Initialy pressure is P1 and final pressure is P3. The total work done is W. Then
View Solution