If O is origin and C is the mid - point of A (2, -1) and B ( -4, 3) . Then value of OC is
ˆi+ˆj
ˆi−ˆj
−ˆi+ˆj
−ˆi−ˆj
The correct Answer is:C
Coordinate of C is (2−42,−1+32)=(−1,1)
∴OC=−ˆi+ˆj.
Topper's Solved these Questions
- VECTOR ALGEBRABOOK - ARIHANT MATHSCHAPTER - VECTOR ALGEBRAEXERCISE - Exercise (More Than One Correct Option Type Questions)
7 Videos
- VECTOR ALGEBRABOOK - ARIHANT MATHSCHAPTER - VECTOR ALGEBRAEXERCISE - Exercise (Statement I And Ii Type Questions)
3 Videos
- VECTOR ALGEBRABOOK - ARIHANT MATHSCHAPTER - VECTOR ALGEBRAEXERCISE - Exercise For Session 3
11 Videos
- TRIGONOMETRIC FUNCTIONS AND IDENTITIESBOOK - ARIHANT MATHSCHAPTER - TRIGONOMETRIC FUNCTIONS AND IDENTITIESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
19 Videos
Similar Questions
Knowledge Check
If Q(a3,4) is the mid-point of the line segement joining the points A(-6, 5) and B(-2, 3), then the value of 'a' is
A4B−6C−8D−12Let A (a,b) be a fixed point and O be the origin of coordionates. If A1 is the mid-point of OA, A2 is the mid- poind of AA1,A3 is the mid-point of AA2 and so on. Then the coordinates of An are
A(a(1−2−n),b(1−2−n))B(a(2n−1−1),b(2−n−1))C(a(1−2(n−1)),b(1−2(n−1)))Dnone of theseIf the origin and the points A(1,2,−2),B(1,−2,3),C(x,y,z) are coplanar, then
A2x+5y+4z=0B2x−5y−4z=0C2x+5y−4z=0D2x−5y+4z=0
A(a+1,a−1),B(a2+1,a2−1) and C(a3+1,a3−1) are given points. D (11, 9) is the mid point of AB and E (41, 39) is the mid point of BC. If F is the mid point of AC then (BF)2 is equal to K2, where K =
View SolutionIf O is the origin and Q is a variable point on y2=x. Find the locus of the mid point of OQ.
View SolutionABCD is a square. E is the mid-point of BC and F is the mid-point of CD . The ratio of the area of triangle AEF to the area of the square ABCD is (a) 1 : 2 (b) 1 : 3 (c) 1 : 4 (d) 3 : 8
View SolutionIn figure given below ∠B=70∘,∠C=60∘,E is the mid point of BC, F is the mid point of AB, then the value of ∠FEB is
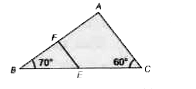
View SolutionIf (a, b) is the mid-point of the line segment joining the points A(10, -6) and B(k, 4) and a-2b = 18, the value of k is:
View Solution
