If G is the centroid of ΔABCandG' is the centroid of ΔA'B'C' then −−→AA'+−−→BB'+−−→CC'=
Video Solution
Text Solution
Here,
G is centroid of ΔABC and G' is centroid of ΔA'B'C', shown as in figure.
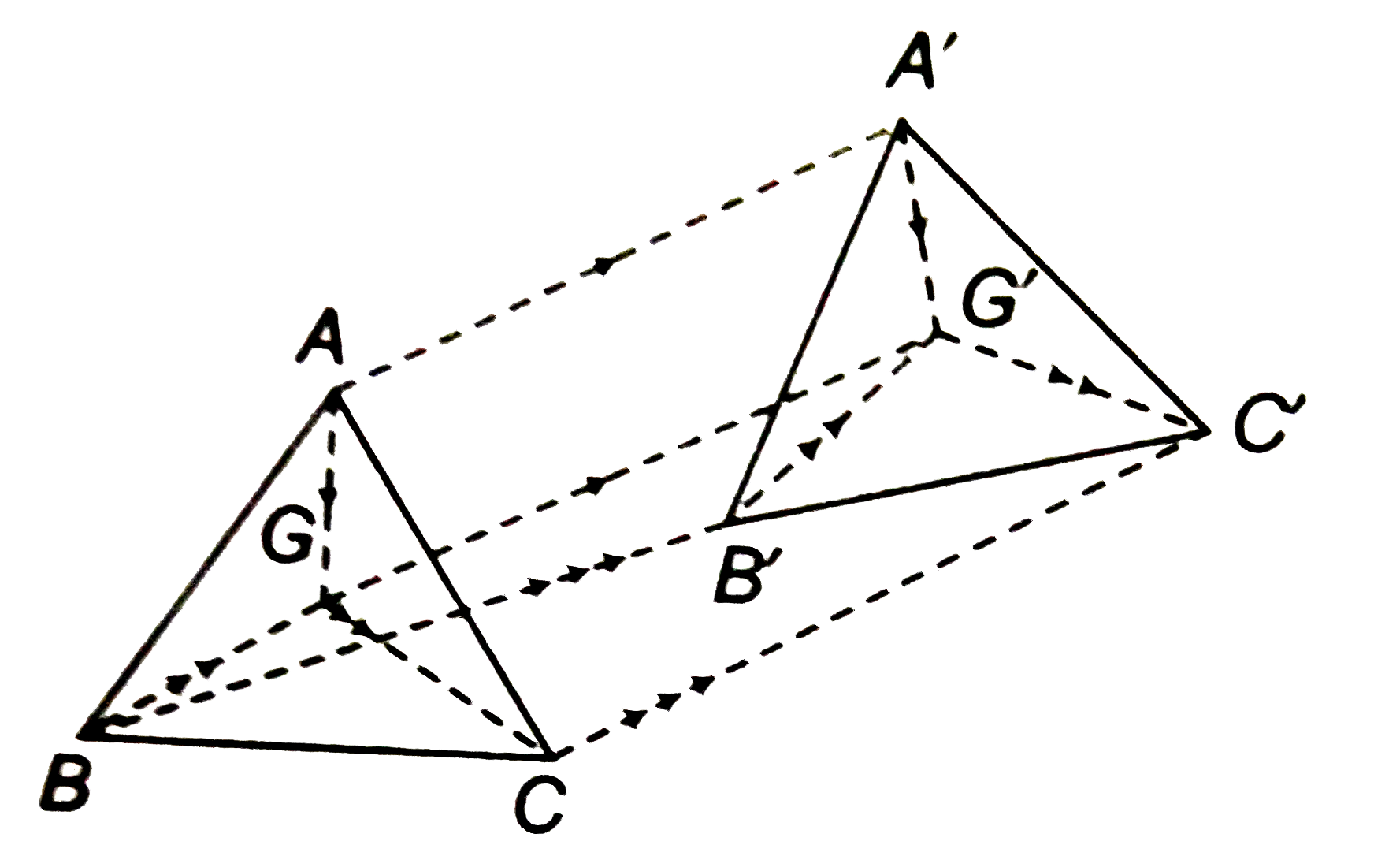
Clearly, AA'=AG+GG'+G'A' (polygon law)
BB'=BG+GG'+G'B'
CC'=CG+CG'+G'C'
On adding these
AA'+BB'+CC'=3GG'+(AG+BG+CG)+(G'A'+G'B'+G'C')
=3GG'+(AG+2DG)+(G'A'+2G'D')
(usingg AD and A'D' as the medians of ΔABC and ΔA'B'C', respectively).
=3GG'+(AG+GA)+G'A'+A'G'
=3GG'+O+O
∴AA'+BB'+CC'=3GG'
|
Topper's Solved these Questions
- VECTOR ALGEBRABOOK - ARIHANT MATHSCHAPTER - VECTOR ALGEBRAEXERCISE - Exercise For Session 1
7 Videos
- VECTOR ALGEBRABOOK - ARIHANT MATHSCHAPTER - VECTOR ALGEBRAEXERCISE - Exercise For Session 2
17 Videos
- TRIGONOMETRIC FUNCTIONS AND IDENTITIESBOOK - ARIHANT MATHSCHAPTER - TRIGONOMETRIC FUNCTIONS AND IDENTITIESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
19 Videos
Similar Questions
Knowledge Check
If A, B, C are vertices of a triangle whose position vectors are →a,→band→c respectively and G is the centroid of ΔABC, then −−→GA+−−→GB+−−→GC, is
A→0B→a+→b+→cC→a+→b+→c3D→a−→b−→c3D, E and F are the mid-points of the sides BC, CA and AB respectively of ΔABC and G is the centroid of the triangle, then −−→GD+−−→GE+−−→GF=
A→0B2−−→ABC2−−→GAD2−−→GCLet O, O' and G be the circumcentre, orthocentre and centroid of a ΔABC and S be any point in the plane of the triangle.
Statement -1: −−−→O'A+−−−→O'B+−−−→O'C=2−−−→O'O
Statement -2: −→SA+−−→SB+−−→SC=3−−→SGAStatement - 1 is True, Statement - 2 is True , Statement - 2 is a correct explanation for Statement - 1.BStatement -1 is True, Statement - 2 is True, Statement -2 is not a correct explanation for Statement - 1.CStatement - 1 is True, Statement - 2 is False.DStatement - 1 is False, Statement - 2 is True.
If G is the centroid of a triangle ABC, prove that →GA+→GB+→GC=→0.
View SolutionProve that G→A+G→B+G→C=→0, if G is the centroid of Δ ABC.
View SolutionIf O is the circumcentre, G is the centroid and O' is orthocentre or triangle ABC then prove that: −−→OA+−−→OB+−−→OC=−−−→OO'
View SolutionIf S is the cirucmcentre, G the centroid, O the orthocentre of a triangle ABC, then −→SA+−−→SB+−−→SC is:
View SolutionLet G be the centroid of Δ ABC , If −−→AB=→a,−−→AC=→b, then the −−→AG, in terms of →aand→b, is
View Solution
