In the Cartesian plane, a man starts at origin and walks a distance of 3 units of the north-east direction and reaches a point P. from P, he walks a distance of 4 units in the north-west direction to reach a point Q. construct the parallelogram OPQR with OP and PQ as adjacent sides. let M be the mid-point of PQ.

The correct Answer is:A, B, C, D
(A) Let ˆiandˆj be the unit vectors along OX and OY respectively.
Now, OP=3 and a∩g≤XOP=45∘ implies that
OP=(3cos45∘)ˆi+(3sin45∘)ˆj=3√2(ˆi+ˆj)
(B) Again ∠XOR=135∘andOR=4 implies that
OR=4√2(−ˆi+ˆj)=2√2(−ˆi+ˆj)
(C) the position vector of Q is given by
OP+PQ=OP+OR=1√2(−ˆi+7ˆj)
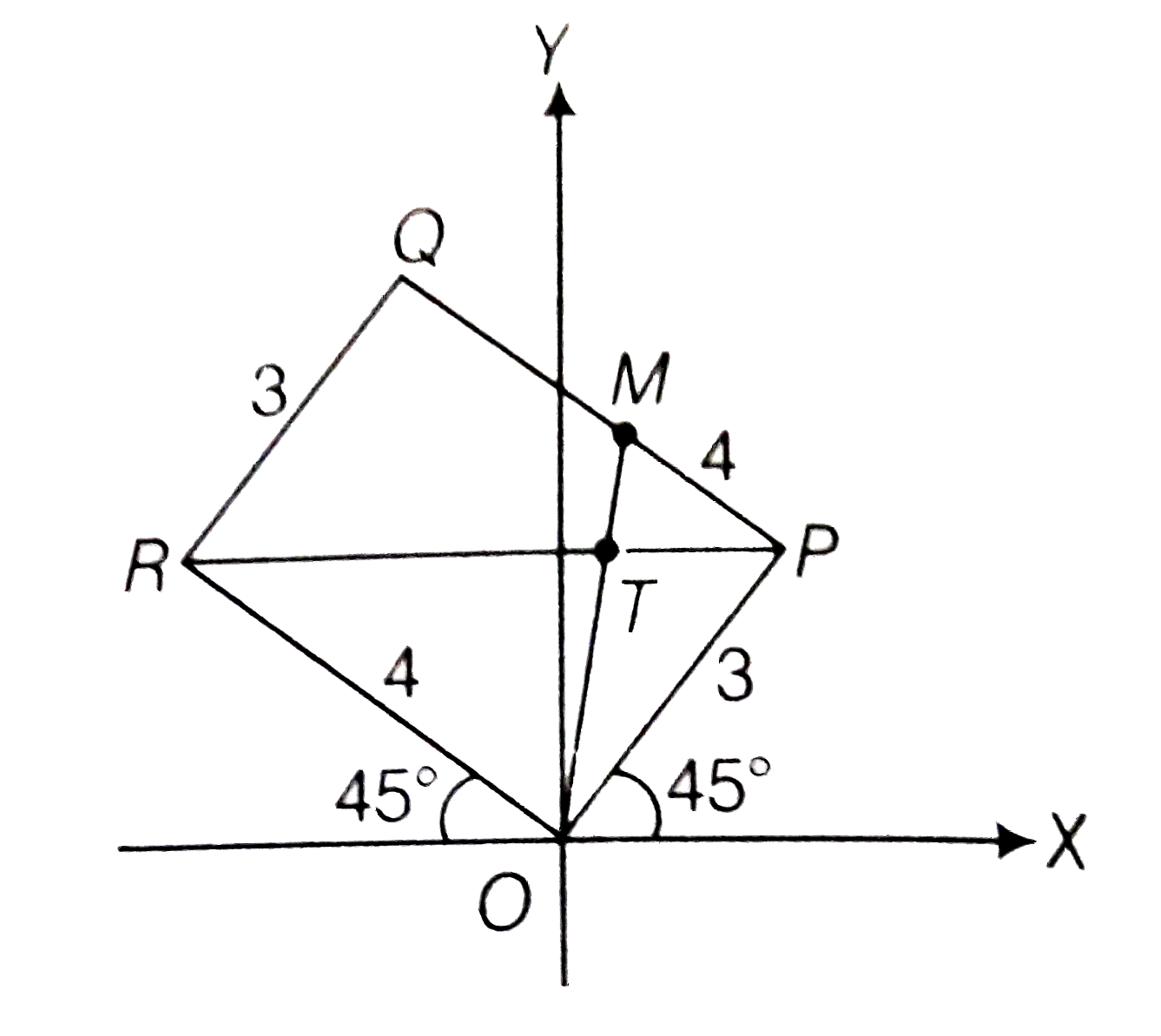
∴OM=(3√2)(ˆi+ˆj)+(1√2)(−ˆi+7ˆj)2
=2ˆi+10ˆj2√2=ˆi+5ˆj√2
(D) Now, PT:RT=1:2
thereofore, OT=1(OR)+2(OP)3
=(4√2)(−ˆi+ˆj)+2[(3√2)(ˆi+ˆj)]3
=√23(ˆi+5ˆj)
Topper's Solved these Questions
- VECTOR ALGEBRABOOK - ARIHANT MATHSCHAPTER - VECTOR ALGEBRAEXERCISE - Exercise For Session 1
7 Videos
- VECTOR ALGEBRABOOK - ARIHANT MATHSCHAPTER - VECTOR ALGEBRAEXERCISE - Exercise For Session 2
17 Videos
- TRIGONOMETRIC FUNCTIONS AND IDENTITIESBOOK - ARIHANT MATHSCHAPTER - TRIGONOMETRIC FUNCTIONS AND IDENTITIESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
19 Videos
Similar Questions
A man walks a distance of 3 units from the origin towards north-east to reach position A. from there he walks a distance of 4 units towards North west to reach position P. Then position of P in argand plane is
View SolutionIn the Cartesian plane, O is the origin of the coordinate axes. A person starts at O and walks a distance of 3 units in the NORTH−EAST direction and reaches the point P. From P he walks 4 units distance of 3 parallel to NORTH−WEST direction and reaches the point Q. Express the vector OQ in terms of iandj (observe that ∣(XOP)=45∘).
View Solution
Knowledge Check
A man walks a distance of 3 units from the origin towards the North-East (N450E) direction.From there, he walks a distance of 4 units towards the North-West (N450W) direction to reach a point P. Then, the position of P in the Argand plane is 3eiπ4+4i (b) (3−4i)eiπ4 (4+3i)eiπ4 (d) (3+4i)eiπ4
A3eiπ/4+4iB(3−4i)eiπ/4C(4+3i)eiπ/4D(3+4i)eiπ/4Let O be the origin and P be the point at a distance 3 units from origin. If direction ratios of OP are (1,-2,-2), then coordinates of P is given by
A(1,-2,-2)B(3,-6,-6)C(1/3,−2/3,−2/3)D(1/9,−2/9,−2/9)Let O be the origin and P be the point at a distance 3 units from origin. If direction ratios of OP are (1,−2,−2), then coordinates of P is given by
A(1,−2,−2)B(3,−6,−6)C(1/3,−2/3,−2/3)D(1/9,−2/9,−2/9)
A man walks a distance of 3 units from the origin towards the North-East (N450E) direction.From there, he walks a distance of 4 units towards the North-West (N450W) direction to reach a point P. Then, the position of P in the Argand plane is 3eiπ4+4i (b) (3−4i)eiπ4 (4+3i)eiπ4 (d) (3+4i)eiπ4
View SolutionA man walks 6 km towards north and turns left and walks 2 kms towards West. If he has started from point Z and reached point A, then what is the shortest distance between point Z and A
View SolutionDirection: Read the following information carefully and answer the question that follow: A person starts walking from Point A and travels 75 km east to reach point B and then takes a left turn and reaches point C after walking 15 km. From there He takes a left turn and walks 55 km and reach point D then again takes a left turn and walk 15 km to reach point H. Then he moves in the same direction in which he was facing and further walks 40 km to reach point E. He then turns in west direction and walks 40 km to reach point F and at last, he takes a right turn and walks 40 km to reach point G. K is 40 km south of A.
At what distance and in which direction is D respect to E?
View SolutionDirection: Read the following information carefully and answer the question that follow: A person starts walking from Point A and travels 75 km east to reach point B and then takes a left turn and reaches point C after walking 15 km. From there He takes a left turn and walks 55 km and reach point D then again takes a left turn and walk 15 km to reach point H. Then he moves in the same direction in which he was facing and further walks 40 km to reach point E. He then turns in west direction and walks 40 km to reach point F and at last, he takes a right nun and walks 40 km to reach point G. K is 40 km south of A.
What is the total distance between point G and point B?
View SolutionDirection: Read the following information carefully and answer the question that follow: A person starts walking from Point A and travels 75 km east to reach point B and then takes a left turn and reaches point C after walking 15 km. From there He takes a left turn and walks 55 km and reach point D then again takes a left turn and walk 15 km to reach point H. Then he moves in the same direction in which he was facing and further walks 40 km to reach point E. He then turns in west direction and walks 40 km to reach point F and at last, he takes a right nun and walks 40 km to reach point G. K is 40 km south of A.
In which direction is K with respect to B?
View Solution
