Let position vectors of point A,B and C of triangle ABC represents be ˆi+ˆj+2ˆk,ˆi+2ˆj+ˆk and 2ˆi+ˆj+ˆk. Let l1+l2 and l3 be the length of perpendicular drawn from the orthocenter 'O' on the sides AB, BC and CA, then (l1+l2+l3) equals
A
2√6
B
3√6
C
√62
D
√63.
Video Solution
Text Solution
The correct Answer is:C
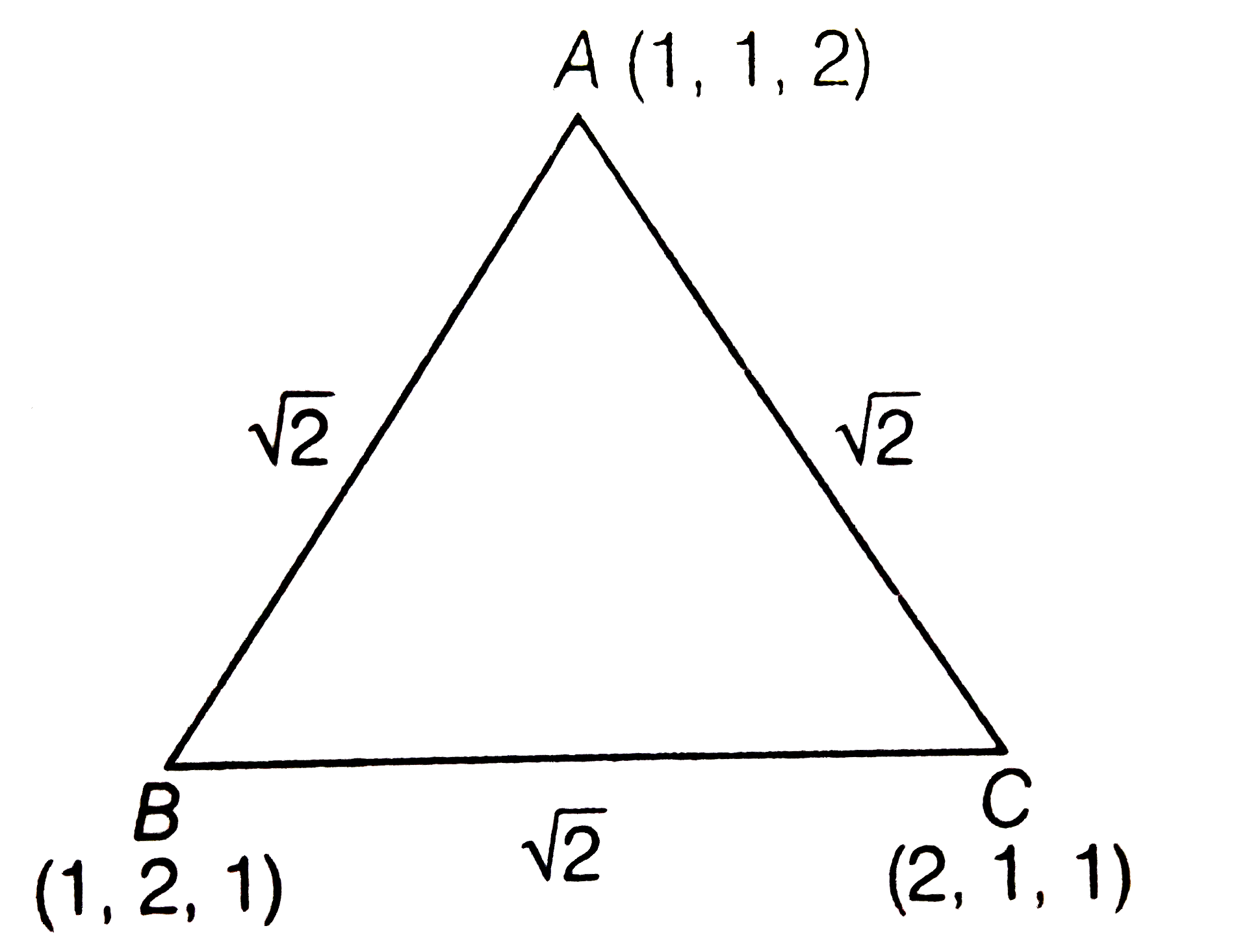
Clearly, triangle formed by the given points ˆi+ˆj+2ˆk,
ˆi+2ˆj+ˆkand2ˆi+ˆj+ˆk is equilateral as AB=BC=AC=√2.
∴Distance of orthocentre 'O' from the sides is equal to inradius of the triangle.
∴l1=l2=l3=inradius=r=Δs=√34(√2)232(√2)=1√6
⇒(l1+l2+l3)=3√6=√62
|
Topper's Solved these Questions
- VECTOR ALGEBRABOOK - ARIHANT MATHSCHAPTER - VECTOR ALGEBRAEXERCISE - Exercise For Session 1
7 Videos
- VECTOR ALGEBRABOOK - ARIHANT MATHSCHAPTER - VECTOR ALGEBRAEXERCISE - Exercise For Session 2
17 Videos
- TRIGONOMETRIC FUNCTIONS AND IDENTITIESBOOK - ARIHANT MATHSCHAPTER - TRIGONOMETRIC FUNCTIONS AND IDENTITIESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
19 Videos
Similar Questions
Knowledge Check
If the position vectors of A, B and C are respectively 2ˆi−ˆj+ˆk,ˆi−3ˆj−5ˆkand3ˆi−4ˆj−4ˆk , then cos2 is equal to
A0B641C3541D1If the position vectors of the vertices of ΔABC are 3ˆi+ˆj+2ˆk,ˆi−2ˆj+7ˆkand−2ˆi+3ˆj+5ˆk, then the ΔABC is
Aright angled and isoscelesBright angled, but not isoscelesCisosceles but not right angledDequilateralIf the position vectors of the vertices of ΔABC are 3ˆi+ˆj+2ˆk,ˆi−2ˆj+7ˆkand−2ˆi+3ˆj+5ˆk, then the ΔABC is
Aright angled and isoscelesBright angled, but not isoscelesCisosceles but not right angledDequilateral
The position vectors of the points A,B and C are (2ˆi+ˆj−ˆk),(3ˆi−2ˆj+ˆk) and (ˆi+4ˆj−3ˆk) respectively. Show that the points A,B and C are collinear.
View SolutionThe position vectors of the points A, B, C are 2ˆi+ˆj−ˆk,3ˆi−2ˆj+ˆkandˆi+4ˆj−3ˆk respectively . These points
View SolutionIf the position vectors of A, B ,C are respectively 2ˆi−ˆj+ˆk,ˆi−3ˆj−5ˆk and 3ˆi−4ˆj−4ˆk then cos2A is equal
View SolutionThe position vectors of the points A, B, and C are ˆi+ˆj+ˆk.ˆi+5ˆj−ˆk and 2ˆi+3ˆj+5ˆk, respectively . The greatest angle of triangle ABC is -
View SolutionThe position vectors of points A,B and C are ˆi+ˆj,ˆi+5ˆj−ˆkand2ˆi+3ˆj+5ˆk, respectively the greatest angle of triangle ABC is
View Solution
