In a quadrilateral PQRS,→PQ=→a,→QR,→b,→SP=→a−→b,M is the midpoint of →QRandX is a point on SM such that SX=45SM. Prove that P,XandR are collinear.
A
PX=15PR
B
PX=35PR
C
PX=25PR
D
none of these
Video Solution
Text Solution
The correct Answer is:B
If we take point P as the origin, the position vectors of Q and S are a and b-a respectively.
In ΔPQR, we have
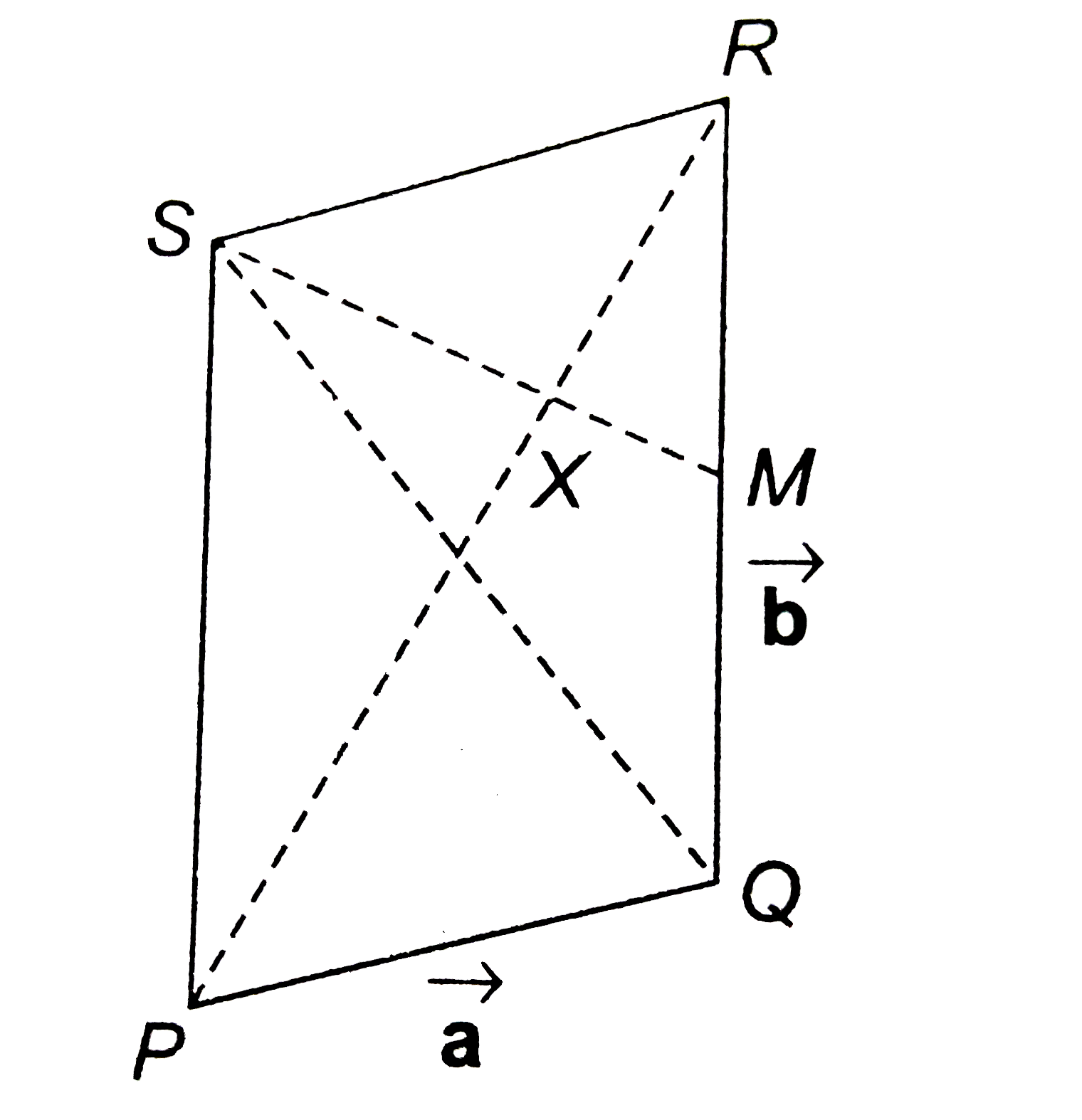
PR=PQ+QR⇒PR=a+b
∴Position vector of R=a+b
⇒PV or M=a+(a+b)2=(a+12b)
Now, SX=45SM
⇒XM=SM−SX=SM−45SM=15SM
∴SX:XM=4:1
⇒PV of X=4(a+12b)+1(b−a)4+1
=3a+2b5⇒PX=35(a+b)
⇒PX=35PR
|
Topper's Solved these Questions
- VECTOR ALGEBRABook:ARIHANT MATHSChapter:VECTOR ALGEBRAExercise:Exercise For Session 1
Explore 7 Videos
- VECTOR ALGEBRABook:ARIHANT MATHSChapter:VECTOR ALGEBRAExercise:Exercise For Session 2
Explore 17 Videos
- TRIGONOMETRIC FUNCTIONS AND IDENTITIESBook:ARIHANT MATHSChapter:TRIGONOMETRIC FUNCTIONS AND IDENTITIESExercise:Exercise (Questions Asked In Previous 13 Years Exam)
Explore 19 Videos
Similar Questions
Knowledge Check
If →P×→Q=→R,→Q×→R=→P and →R×→P=→Q then
A→P,→Q and →R are coplanarBangle between →P and →Q may be less than 90∘C→P+→Q+→R cannot be equal to zero.D→P,→Q and →R are mutually perpendicularif →P×→R=→Q×→R, then
A→P=→QB→P and →Q need not be equalCThere are infinite number of possibilities for →P (If →Q and →R are given ) which satisfy this relationship.D→p and →Q must be coplanarIf →Pand→Q are two vectors, then the value of (→P+→Q)×(→P−→Q) is
A→P×→QB−(→P×→Q)C2(→Q×→P)D+2(→P×→Q)
If →r=3→p+4→q and 2→r=→p−3→q then
View SolutionIf →P+→Q=→R and ∣∣→P∣∣=∣∣→Q∣∣=∣∣→R∣∣, then angle between →P and →Q is
View SolutionIf →p×→q=→rand→p⋅→q=c, then →q is
View SolutionFor three vectors →p,→q and →r if →r=3→p+4→q and 2→r=→p−3→q then
View SolutionIf ∣∣→P×→Q∣∣=PQ then the angle between →Pand→Q is
View Solution