If C is the middle point of AB and P is any point outside AB, then
PA+PB=PC
PA+PB=2PC
PA+PB+PC=0
PA+PB+2PC=0
The correct Answer is:B
PA+PB=(PA+AC)+(PB+BC)−(AC+BC)
=PC+PC−(AC−CB)=2PC−0 (∵AC=CB)
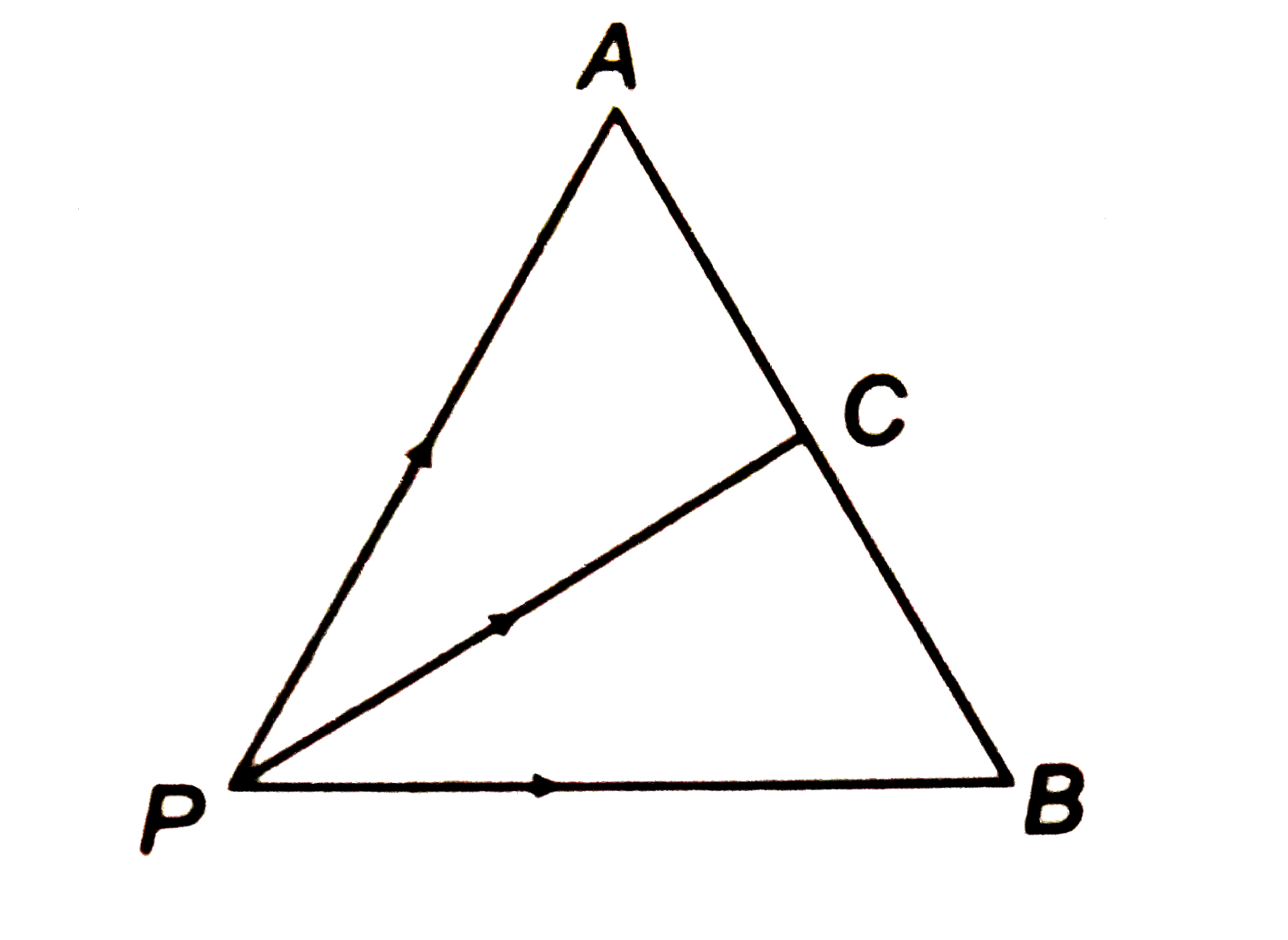
∴PA+PB=2PC
Topper's Solved these Questions
- VECTOR ALGEBRABook:ARIHANT MATHSChapter:VECTOR ALGEBRAExercise:Exercise For Session 1
Explore 7 Videos
- VECTOR ALGEBRABook:ARIHANT MATHSChapter:VECTOR ALGEBRAExercise:Exercise For Session 2
Explore 17 Videos
- TRIGONOMETRIC FUNCTIONS AND IDENTITIESBook:ARIHANT MATHSChapter:TRIGONOMETRIC FUNCTIONS AND IDENTITIESExercise:Exercise (Questions Asked In Previous 13 Years Exam)
Explore 19 Videos
Similar Questions
Knowledge Check
If C is the mid-point of AB and P is any point outside AB, then
APA + PB = PCBPA + PB + 2 PC = 0CPA + PB - 2PC = 0DPA + PB + PC = 0If C is the mid-point of AB and P is any point outside AB, then
APA+PB+PC=0BPA+PB+2PC=0CPA+PB=PCDPA+PB=2PCWhich of the following statements are correct :- If M is the mid point of AB and O is any point, then
AOM=OA+MABOM=OA−MACOM=12(OA−OB)DOM=12(OB+OA)
In the given figure, in △ABC, D is the mid-point cf AB and P is any point on BC. If CQ∣∣PD meets AB in Q and area of △ABC=30cm2, then, area of △BPQ is
View SolutionIf →C is the midpoint of −−→ABand→P is any point outside −−→AB, then −−→PA+−−→PB=
View SolutionAB is a vertical pole. The end A is on the level ground .C is the middle point of AB. P is a point on the level ground . The portion BC subtends an angles β at P. If AP = nAB, then tan β=
View SolutionAB is a vertical pole. The end A is on the level ground .C is the middle point of AB. P is a point on the level ground . The portion BC subtends an angles β at P. If AP = nAB, then tan β=
View SolutionLet a vertical tower AB have its end A on the level ground. Let C be the mid-point of AB and P be a point on the ground such that AP = 2AB. If √BPC=β, then tan β is equal to
View Solution