If ABCDEF is a regular hexagon, prove that AD+EB+FC=4AB.
Video Solution
Text Solution
We have,
AD+EB+FC=(AB+BC+CD)+(ED+DC+CB)+FC
=AB+(BC+CB)+(CD+DC)+ED+FC
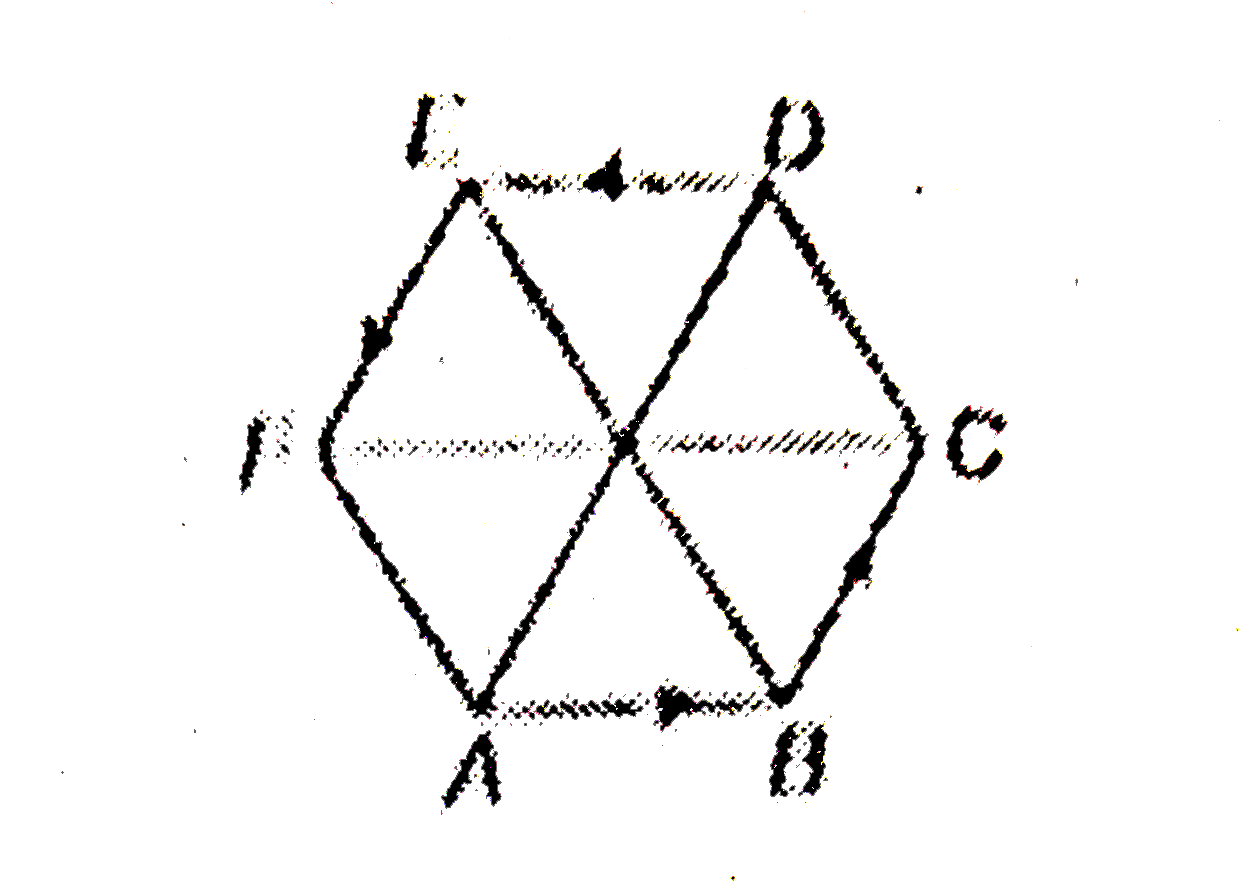
=AB+O+O+AB+2AB=4AB
(∵ED=AB,FC=2AB) hence proved.
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - ARIHANT MATHSCHAPTER - VECTOR ALGEBRAEXERCISE - Exercise For Session 17videos
VECTOR ALGEBRA
- BOOK - ARIHANT MATHSCHAPTER - VECTOR ALGEBRAEXERCISE - Exercise For Session 217videos
VECTOR ALGEBRA
- BOOK - ARIHANT MATHSCHAPTER - TRIGONOMETRIC FUNCTIONS AND IDENTITIESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)19videos
TRIGONOMETRIC FUNCTIONS AND IDENTITIES
Similar Questions
Knowledge Check
- Question 1 - Select One
If ABCDEF is a regular hexagon, then ΔACE is
Aa right-angled triangleBan obtuse-angled triangleCan isosceles triangleDan equilateral triangle - Question 2 - Select One
If ABCDEF is regular hexagon, then AD+EB+FC is equal to
A0B2ABC3ABD4AB - Question 3 - Select One
If ABCDEF is a regular hexagon , then A→D+E→B+F→C equals
A2A→BB→0C3A→BD4A→B
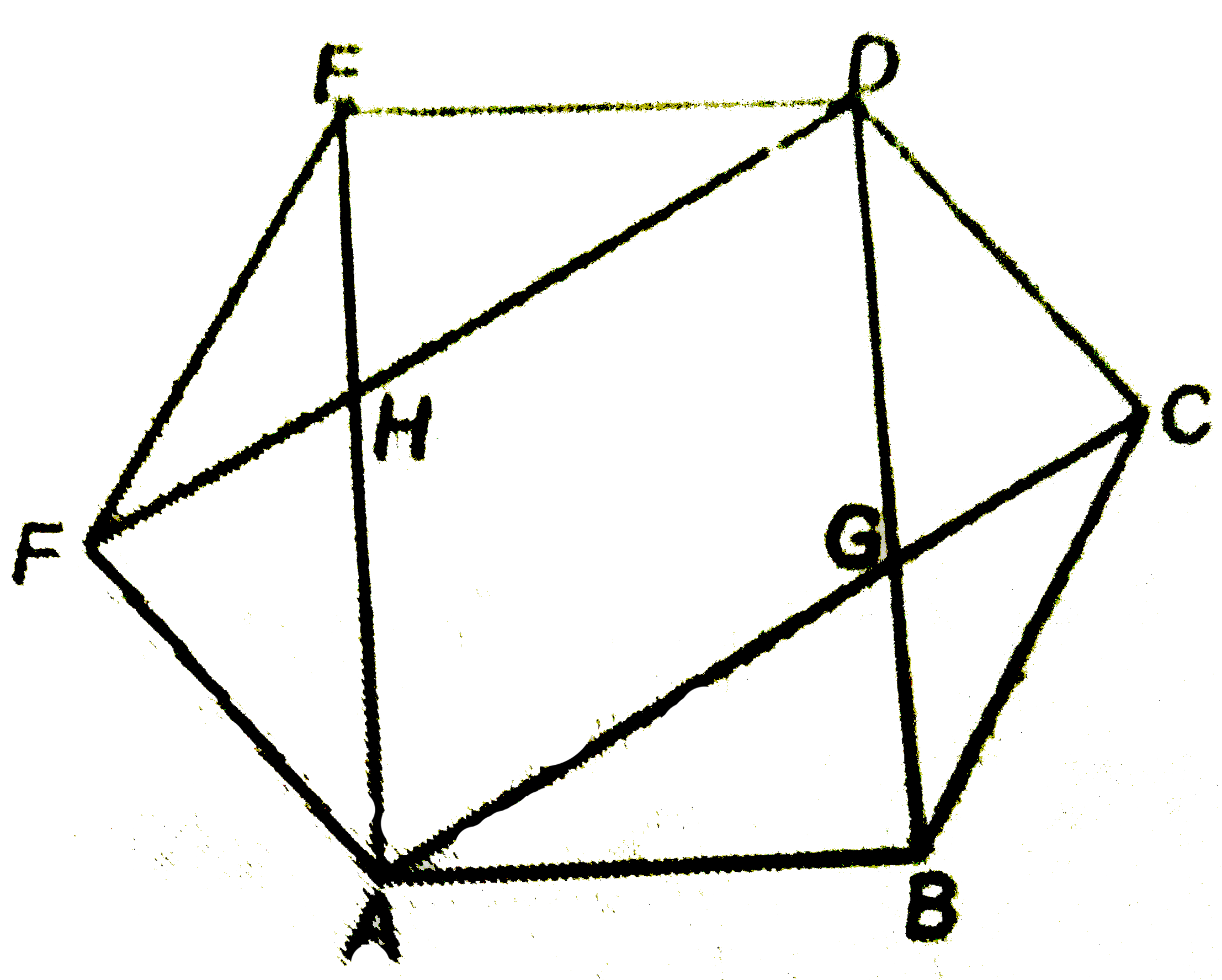
In the adjoining figure, ABCDEF is a regular hexagon. Prove that □ABDE,□ACDFand□AGDH are parallelograms.
 View Solution
View SolutionIn Fig. ABCDEF is a ragular hexagon. Prove that
−−→AB+−−→AC+−−→AD+−−→AE+−−→AF=6−−→AO.View SolutionIf ABCDEF is a regular hexagon of side a, then ¯¯¯¯¯¯AB.¯¯¯¯¯¯AF=
View SolutionIf ABCDEF is a regular hexagon, then what is the value (in degrees) of ∠ADB?
View SolutionIf ABCDEF is a regular hexagon, then what is the value (in degrees) of ∠ADB?
View Solution

