The sets S and E are defined as given below:
and
.
Show that .
Video Solution
Text Solution
Graph of S
Similarly,
So, S consists of all points inside the square (not on , 4 and , 4) bounded by the lines x = 2, y = 2, x = 4 and y = 4.
Graph of R
So, E consists of all points inside and on the ellipse with centre (4, 3) and semi-major and semi-minor axes are 3 and 2, respectively.
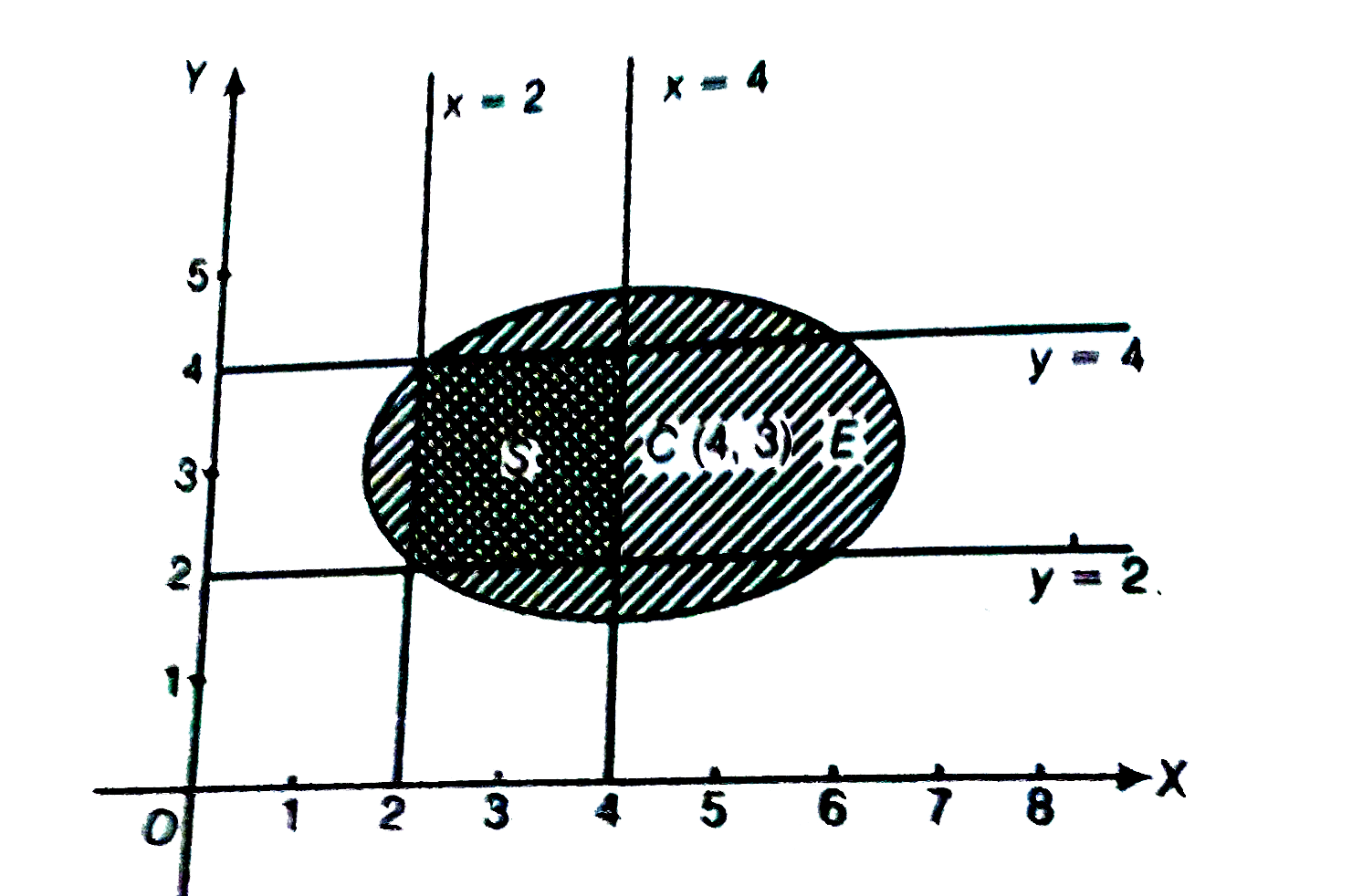
From the above graph, it is evident that the double hatched (which is S) is within the region represented by E. i.e.,
|
Topper's Solved these Questions
- SETS, RELATIONS AND FUNCTIONS Book:ARIHANT MATHSChapter:SETS, RELATIONS AND FUNCTIONS Exercise:Exercise For Session 1
Explore 11 Videos
- SETS, RELATIONS AND FUNCTIONS Book:ARIHANT MATHSChapter:SETS, RELATIONS AND FUNCTIONS Exercise:Exercise For Session 2
Explore 10 Videos
- SEQUENCES AND SERIESBook:ARIHANT MATHSChapter:SEQUENCES AND SERIESExercise:Exercise (Questions Asked In Previous 13 Years Exam)
Explore 38 Videos
- THE STRAIGHT LINESBook:ARIHANT MATHSChapter:THE STRAIGHT LINESExercise:Exercise (Questions Asked In Previous 13 Years Exam)
Explore 18 Videos
Similar Questions
Knowledge Check
Let S be the relation on N defined by:
S={(x,y):y2≤x≤2y}. Then S is:Areflexive onlyBtransitive onlyCsymmetric onlyDreflexive and symmetricThe relation R defined on the set A = {1,2,3,4, 5} by
R ={(x, y)} : ∣∣x2−y2∣∣<16} is given byA{(1,1), (2, 1), (3, 1),(4, 1), (2,3)}B{(2,2), (3,2),(4,2), (2,4)}C{(3,3), (3,4), (5,4), (4, 3), (3, 1)}DNone of theseLet P and T be the subsets of X-y plane defined by
fP={(x,y):x≤0,y and x2+y2=1}
T={(x,y):x>0,y>0 and x8+y8<1} then P∪T isAthe void set ΦBPCTDP−Tc
Find the area bounded by the region given by:
A={(x,y):(x,y):x225+y29≤1<x5+y3}.
View SolutionLet S={(x,y):x29+y24≤1} and T={xy|x∣≤3 and |y|≤2}
View SolutionLet S be the area of the region enclosed by y=e−x^2,y=0,x=0,andx=1. Then S≥1e (b) S≥1=1e S≤14(1+1√e) (d) S≤1√2+1√e(1−1√2)
View SolutionEquation x2y2−9y2+6x2y−54y=0 represents
View SolutionThe coentre of the ellipse 4x2+9y2−16x−54y+61=0 is
View Solution