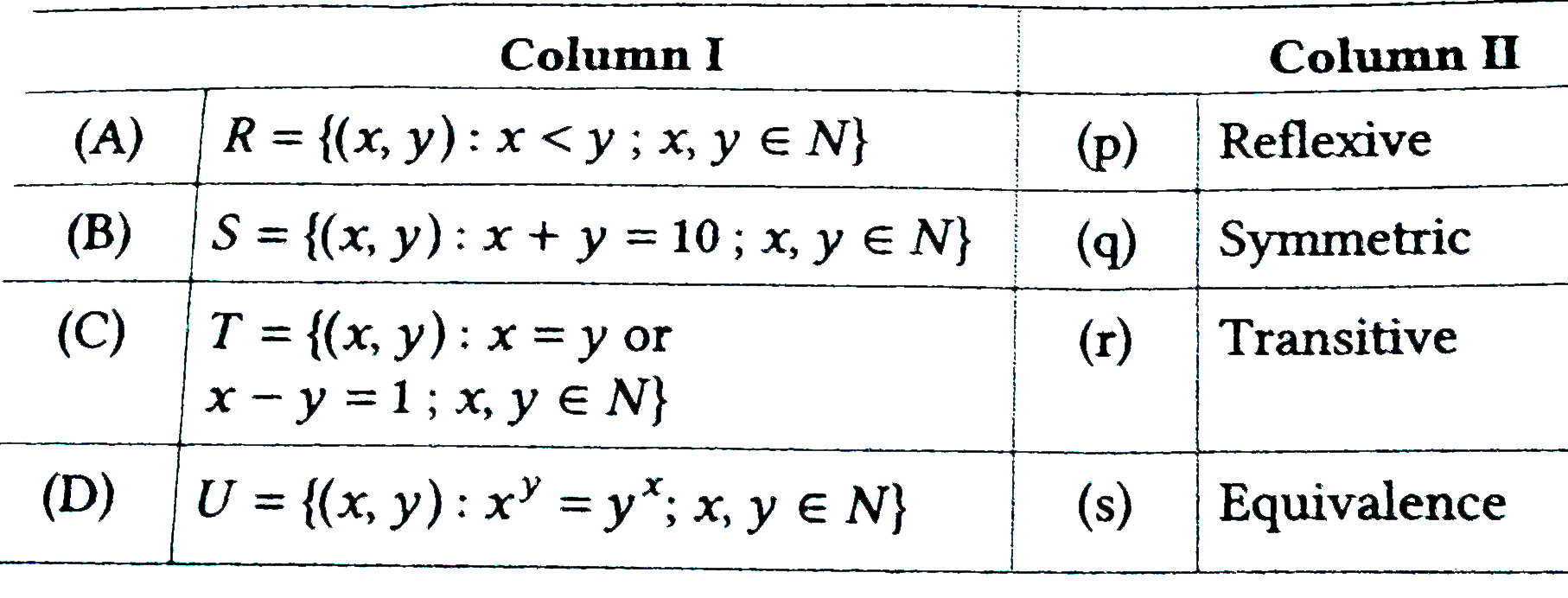The correct Answer is:(A) → (r ); (B) → (q); (C) → (p); (D) → (p,q,r,s)
(A) ∵R={(x,y):x<y,x,y∈N}
xcancelltxtherefore(x,x)cancelinR
So, R is not reflexive.
Now, (x,y)inRimpliesxltycancelimpliesyltximplies(y,x)cancelinR
∴ R is not symmetric.
Let (x, y) ∈R and (y, z) ∈ R
⇒x<yandy<z⇒x<z⇒(x,z)∈R
∴R is transitive.
(B) ∵S={(x,y):x+y=10,x,y∈N}
∴x+x=10⇒2x=10⇒x=5
So, each element of N is not related to itself by the relation x + y = 10.
∴S is not reflexive.
Now, (x,y)∈S⇒x+y=10⇒y+x=10
⇒(y,x)∈S
∴S is symmetric relation.
Now, let (3,7)inS and (7,3)inSimplies(3,3)cancelinS
∴ S is not transitive.
(C ) ∵T={(x,y):x=yorx−y=1,x,y∈N}
∴x=x
So, (x,x)∈T,∀x∈N
∴ T is reflexive.
Let (3,2)∈Tand3−2=1
cancelimplies2-3=-1implies(2,3)cancelinT
∴ T is not symmetric.
Now, let (3,2)∈Tand(2,1)∈T
∴3−2=1and2−1=1
Then, (3,1)cancelinT" "[because3-1=2ne1]
∴ T is not transitive.
(D) U={(x,y):xy=yx,x,y∈N}
∵xx=xx
∴(x,x)∈U
∴U is reflexive.
Now, (x,y)∈U⇒xy=yx
⇒yx=xy⇒(y,x)∈U
∴ U is symmetric.
Now, let (x,y)∈Uand(y,z)∈U
⇒xy=yxandyz=zy
Now, (xy)z=(yx)z
⇒(xz)y=(yz)x⇒(xz)y=(zy)x
⇒(xz)y=(zx)y⇒xz=zx⇒(x,z)∈U
∴U is transitive.
Hence, U is an equivalence relation.
Topper's Solved these Questions
- SETS, RELATIONS AND FUNCTIONS BOOK - ARIHANT MATHSCHAPTER - SETS, RELATIONS AND FUNCTIONS EXERCISE - Exercise For Session 1
11 Videos
- SETS, RELATIONS AND FUNCTIONS BOOK - ARIHANT MATHSCHAPTER - SETS, RELATIONS AND FUNCTIONS EXERCISE - Exercise For Session 2
10 Videos
- SEQUENCES AND SERIESBOOK - ARIHANT MATHSCHAPTER - SEQUENCES AND SERIESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
38 Videos
- THE STRAIGHT LINESBOOK - ARIHANT MATHSCHAPTER - THE STRAIGHT LINESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
18 Videos
Similar Questions
If X={4n−3n−1:n∈N}andy={9(n−1):n∈N}, then X∪Y equals
View SolutionIf A = {2, 3, 5}, B = {2, 5, 6}, then (A−B)×(A∩B) is
View SolutionLet a,b,c be in A.P. and |a|<1,|b|<1|c|<1. If x=1+a+a2+....to ∞,y=1+b+b2+....to ∞and,z=1+c+c2+...to ∞, then x,y,z are in
View SolutionThe lines parallel ot the x-axis and passing through the intersection of the lines ax+2by+3b=0andbx−2ay−3a=0 [where(a,b)≠(0,0)] is-
View SolutionIdentify the cell organelle 'A' :-
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/ALN_BIO_C10_E08_018_Q01.png" width="80%"gt
View SolutionHow many lines of symmetry does the above figure have ?
View SolutionWhich of the following are correct chain isomers of butane ? (i)
View SolutionDetermine the point of symmetry of a regular hexagon.
View SolutionDtermine the images of the following figure about the given line :
View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionFind the area of the figure given below.

View SolutionThe area of the shaded part in the figure given below is ______.

View SolutionThe inequation represented by the graph given below is :
View SolutionThe inequation that best describes the graph given below is _________
View Solution