Let R be a relation such that R={(1,4),(3,7),(4,5),(4,6),(7,6)}, find
(i) R−1OR−1 and (ii) (R−1OR)−1

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

(i) We know that, (ROR)−1=R−1OR−1
Dom (R ) = {1, 3, 4, 7}
Range (R ) = {4, 5, 6, 7}
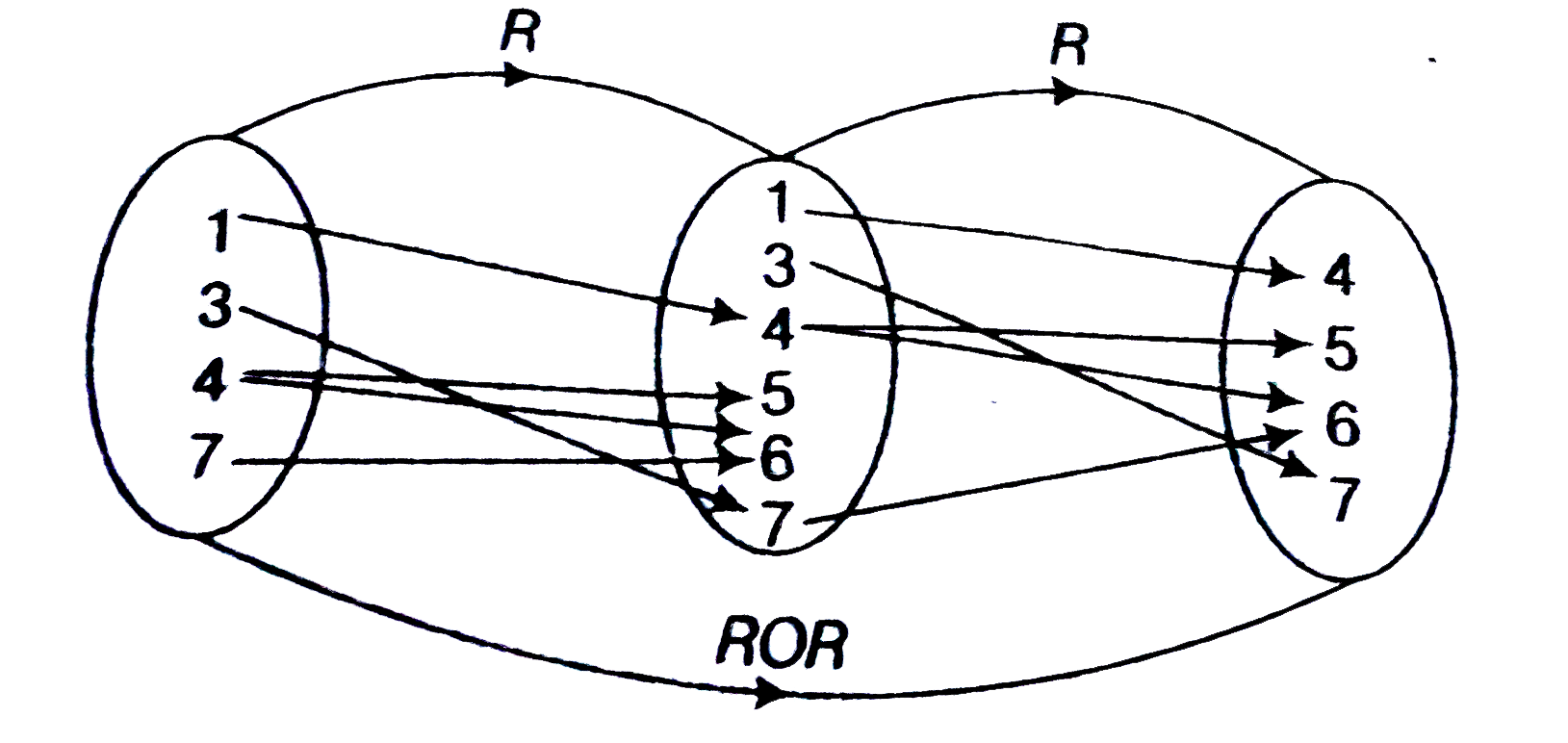
ocr_image
We see that,
1→4→5⇒(1,5)∈ROR
1→4→6⇒(1,6)∈ROR
3→7→6⇒(3,6)∈ROR
∴ROR={(1,5),(1,6),(3,6)}
Then, R−1OR−1=(ROR)−1
={(5,1),(6,1),(6,3)}
(ii) We know that, (R−1OR)−1=R−1O(R−1)−1=R−1OR
Since,
R={(1,4),(3,7),(4,5),(4,6),(7,6)}
∴R−1={(4,1),(7,3),(5,4),(6,4),(6,7)}
∴ Dom (R ) = {1, 3, 4, 7}, Range (R ) = {4, 5, 6, 7}
Dom (R−1)={4,5,6,7}, Range (R−1) = {1,3,4,7}
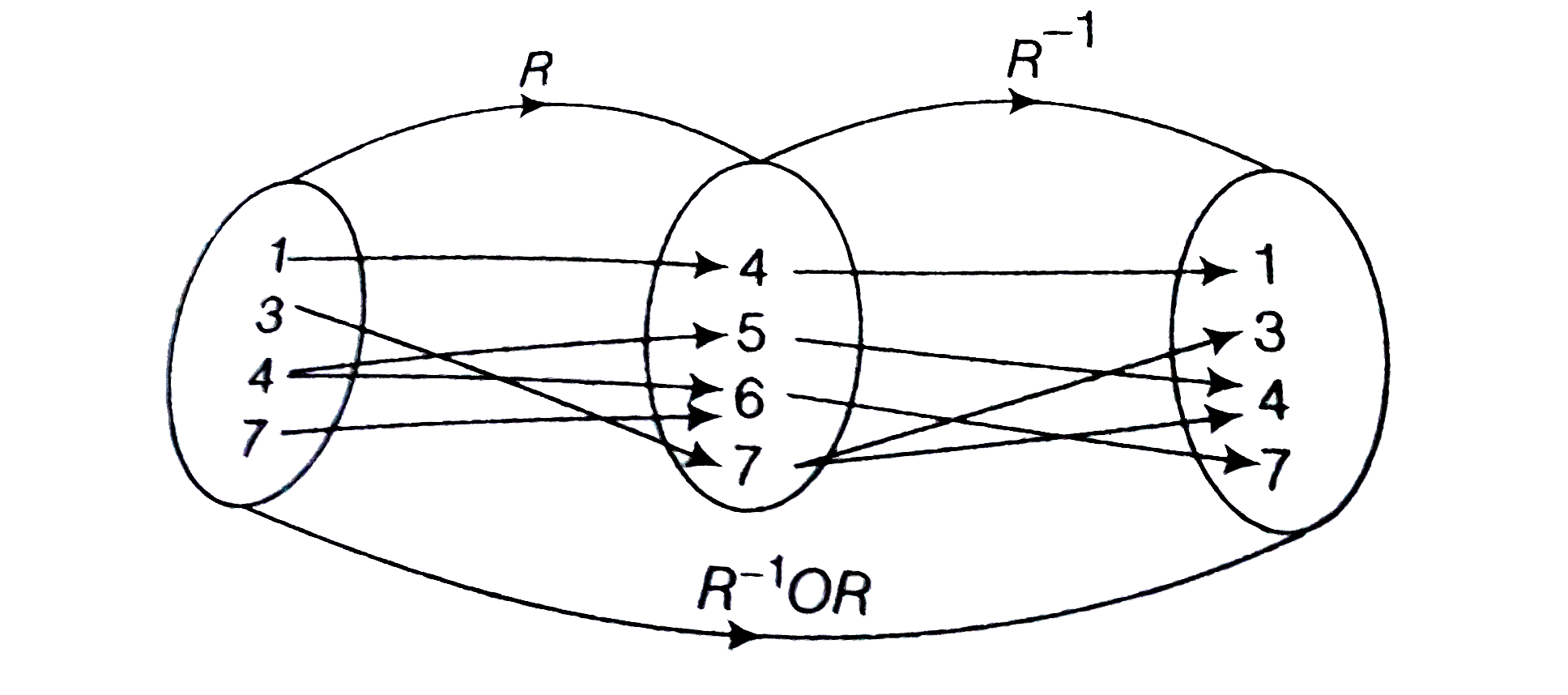
ocr_image
We see that,
1R−−→4R−1−−→1⇒(1,1)∈R−1OR
3R−−→7R−1−−→3⇒(3,3)∈R−1OR
4R−−→5R−1−−→4⇒(4,4)∈R−1OR
4R−−→6R−1−−→4⇒(4,4)∈R−1OR
4R−−→6R−1−−→7⇒(4,7)∈R−1OR
7R−−→6R−1−−→4⇒(7,4)∈R−1OR
7R−−→6R−1−−→7⇒(7,7)∈R−1OR
∴R−1OR={(1,1),(3,3),(4,4),(7,7),(4,7),(7,4)}
Hence, (R−1OR)−1=R−1OR={(1,1),(3,3),(4,4),(7,7),(4,7),(7,4)}

Updated on:21/07/2023
|
Class 12MATHSSETS, RELATIONS AND FUNCTIONS

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • Set builder form of the relation
    R={(−2,−7),(−1,−4),(0,−1),(1,2),(2,5)} is

    A{(a,b):b=2a−3,a,b,∈Z}
    B{(x,y):y=3x−1,x,y∈Z}
    C{(a,b):b=3a−1,a,b∈N}
    D{(u,v):v=3u−1,−2≤u<3andu∈Z}

  • There are three relations R1,R2 and R3 such that R1={(2,1),(3,1),(4,2),R2={(2,2),(2,4),(3,3),(4,4)} and R3={(1,2),(2,3),(3,4),(4,5),(5,6),(6,7)} Then,

    AR1 and R2 are functions
    BR2 and R3 are functions
    CR1 and R3 are functions
    DOnly R1 is a function