Question

Prove by induction that if n is a positive integer not divisible by 3. then ${\displaystyle 3^{2n}+3^n+1}$ is divisible by 13.

Explanation

Let `P(n)=3^(2n)+3^(n)+1, forall n ` is a positive integer not divisible by 3 .
Step I For `n=1`.
`P(1)=3^2+3+1=9+3+1=13`, which is divisible by 13.
Therefore , P(1) is true .
Step II Assume P(n) is true For `n=k, k` is a positive integer not divisible by 3. then
`P(k)=3^(2k)+3^(k)+1`. is divisible by 13.
`rArr P(k)=13r`, where r is an integer .
Step III For `n=k+1`,
`P(k+1)=3^(2(k+1))+3^(k+1)+1`
`=3^2.3^2k+3.3^k+1`

`rArr P(k+1)=3^2(3^(2k)+3^k+1)-6.3^k-8`
`=9P(k)-2(3^(k+1)+4)`
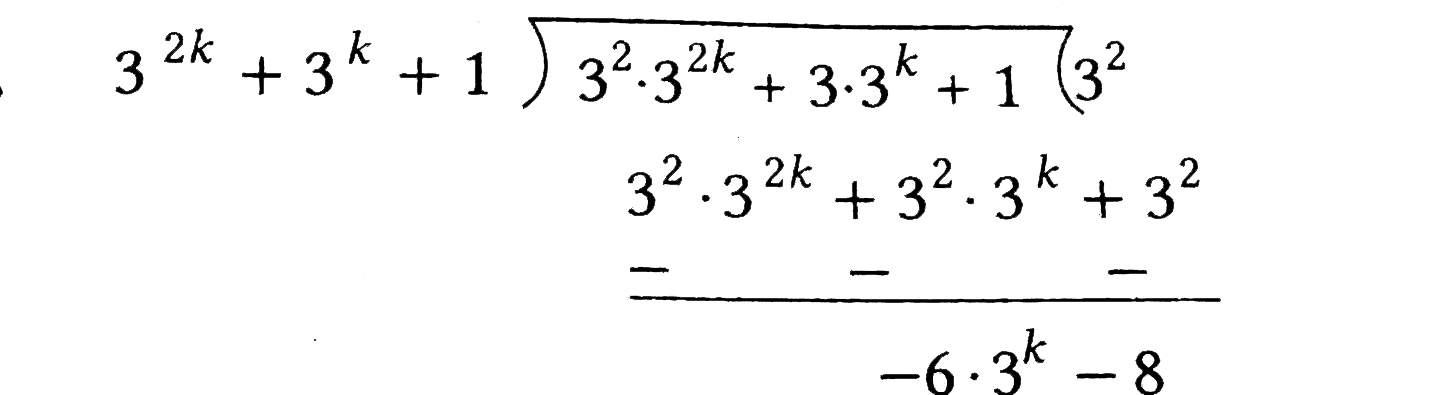
`=9*13r)-2(3^(k+1)+4)` [by assumption step]
which is divisible by 13 as `3^(k+1)+4` is also divisible by `13, forall k in N`. and not divisible by 3. This shows that the result is true for `n=k+1`. Hence , by the principle of mathematical induction , the result is true for all natural numbers not divisible by 3.